LC0aA5 Proofs of the Pythagorean Theorem
Robert W. Lawler
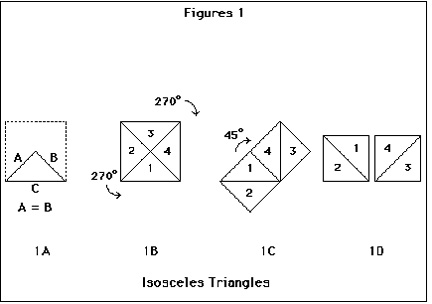
Figure 1 demonstrates the correctness of the Pythagorean theorem for the specific case of the isosceles triangle. The mental actions involved in “seeing” the equivalence of the two smaller squares to that on the hypoteneuse are primarily manipulative in character. Division of the large square with diagonals (1b), the rotations of the triangular quarters of the large square to form the two smaller squares (1c), and the rotation and separation of the set of small squares (1d) are actions such as one might perform with hands upon physical objects. Figure 2 exhibits the generalization of this specific proof to non-isosocles right triangles. Following Figure 2a, one observes that the little square in the center of the larger figure (2b) is exactly what is needed to complete the larger of the two squares constructed on the longer of the two side
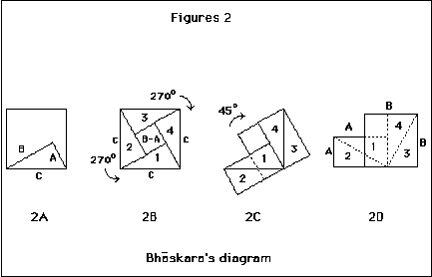
The visual component of understanding is also clearly implicated. Heath (1956, p. 355) notes that the Indian mathematician Bhaskara asserts this proof by introducing the figure and remarking “See !” Observing by inspection of this same figure that one may write also
C2 = 4 (A * B / 2) + (B – A)2
permits one to see the same figure as the foundation of a language-rooted argument from the expansions and manipulation of the algebraic formula as follows:
C2 = 2 A * B + B2 – 2 A * B + A2
C2 = B2 + A2
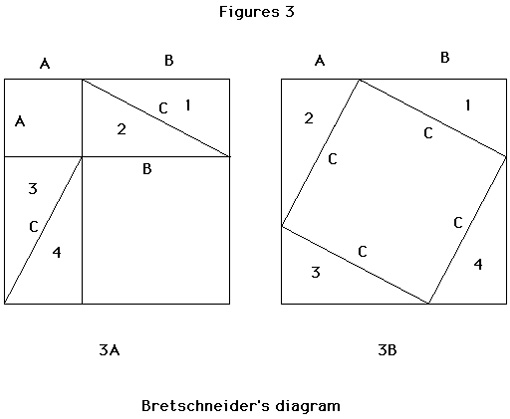
The proof represented by Figure 3, wherein the four triangles in the first frame of are the excess in the square (A + B) beyond the area of A2 and B2, is also based on manipulation. When the four triangles are arranged with their adjacent sides forming the perimeter of the second square (A+B), the “hypotenuse square” (C2) emerges in the center. Since the four triangles of the first frame were the excess area beyond (A2 + B2), their subtraction from the square (A+B)2 of the second frame leaves C2 equal to A2 + B2.
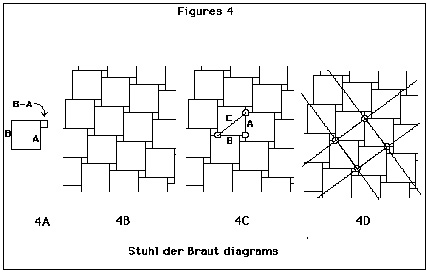
Lietzmann (1953) describes a proof that almost purely visual in character. He starts with the surprising fact that the “Stuhl der Braut” (bride’s-stool, figure 4a), composed of squares based on the sides of any right triangle is suitable for tiling the plane (4b). He observes that a second tiling of the plane with a square lattice can be defined over the bride’s stool lattice, one whose unit square sizes are determined by selecting points of the background lattice. Choosing a unit size based on corners of the large and small sqaures defines the unit length of the square lattice as the hypotenuse of the right triangle (4c). The foreground lattice covers the plane as well. When moved without deformation, each cell of the foreground lattice provides a window onto the background lattice — through which in one position we can see Bhaskara’s diagram (2b) or , with different shifts, those of other figures used in other proofs of the theorem.
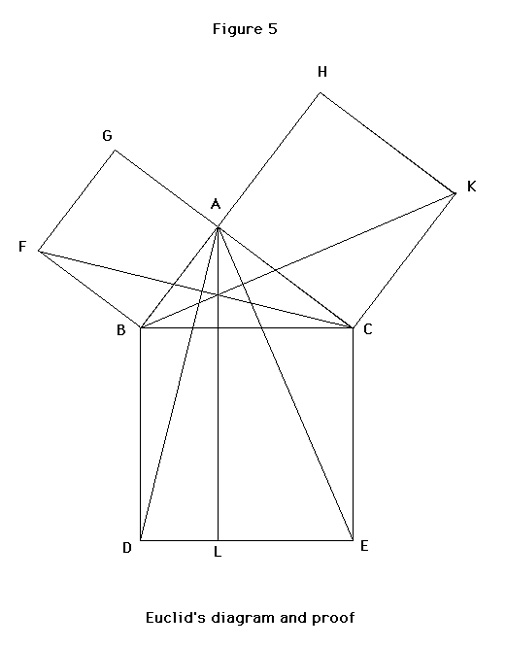
the text of Euclid’s Proof (from Heath. pp. 349-350)
In right-angled triangles, the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
Let ABC be a right-angled triangle having the angle BAC right.
I say that the square on BC is equal to the squares on BA, AC.
For let there be described on BC the square BDEC, and on BA, AC the squares GB, HC; through A let AL be drawn parallel to either BD or CE, and let AD, FC be joined.
Then, since each of the angles BAC, BAG is right, it follows that with a straight line BA, and at the point A on it, the two straight lines AC, AG not lying on the same side make the adjacent angles equal to two right angles; therefore CA is in a straight line with AG.
For the same reason BA is also in a straight line with AH.
And, since the angle DBC is equal to the angle FBA: for each is right: let the angle ABC be added to each; therefore the whole angle DBA is equal to the whole angle FBC. And since DB is equal to BC, and FB to BA, the two sides AB, BD are equal to the two sides FB, BC respectively, and the angle ABD is equal to the angle FBC; therefor the base AD is equal to the base FC, and the triangle ABD is equal to the triangle FBC.
Now the parallelogram BL is double of the triangle ABD for they have the same base BD and are in the same parellels BD, AL.
And the square GB is double of the triangle FBC, for they again have the same base FB and are in the same parel;lels FB, GC.
But the doubles of equals are equal to one another.
Therefore the parallelogram BL is also equal to the square GB.
Similarly, if AE, BK be joined, the parallelogram CL can also be proved equal to the square HC;
therefore the whole square BDEC is equal to the two squares GB, HC.
And the square BDEC is described on BC, and the squares GB, HC on BA, AC.
Therefore the square on the side BC is equal to the squares on the sides BA, AC.
Therefore etc. Q.E.D.
Euclid’s Proof: Contrast with these proofs of Figures 1-4, the proof of Figure 5, Euclid’s own (proposition I.47 in Heath, 1956, pp. 349-350). The proofs of Figure 1-4 are more accessible and obvious than that of Figure 5. Why ? (Proclus praises this proof above that of Pythagoras himself for being both succinct and lucid; the following critical comments are intended to be comparative and illuminating. Euclid’s reputation is , of course, beyond tarnishing by any criticism of mine.) Reading Wertheimer (1959) inclines us to ask “Why is this proof so difficult and ugly ?” The difficulties I find in the proof of Figure 5 are these:
– the proof uses proposition I.41, which asserts that a triangle with the same base and a vertex on a line extending the opposite side of a parallelogram has an area equal to one half that of the parallelogram. (This may not be obvious itself.)
– the single diagram is confusing, cluttered by the lines forming the triangles ABD, FBC
– the strategy of attack is not indicated before one plunges into constructions; on a first encounter, who would guess what triangles ABD and FBC are for ?
– the proof has a “parallel” character in that arguments are made about pointwise equivlances; this stepwise progress and the diagram labelling involve a constant shifting back and forth between visual actions and verbal arguments tied to letter-string-names.
Even when one understands the proof strategy and believes the invoked proposition I.41, the diagram clutter and the cross-modal arguments remain impediments to the unified apprehension possible given the proofs of Figure 1-4.
Locomotion Oriented Discussions
The proofs discussed so far have exhibited significant language, visual, and manipulative components. What about locomotive arguments ? What might a walkabout proof be like ? Figure 6 sets out a locomotion-oriented diagram of the Pythagorean theorem. It does not claim to be a proof. Indeed, it amounts to no more than a statement of the problem, but that statement is cast in terms that directly involve locomotion-related mental action.
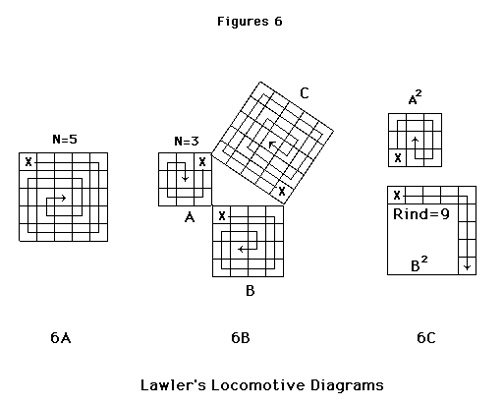
Working from a simple case with natural numbers, one can measure the area of the square in terms of distance travelled by walking forward and depositing unit tiles along the path. After traversing the triangle side (laying down N tiles), the remaining rectangular figure can be exhaustively covered by repeating a simple procedure; move forward N-1 steps, turn 90 degrees, move forward N-1 steps, turn 90 degrees, decrement N by 1. As N goes to zero, we have the square’s area thus:
A (n) = N + 2 * ∑ k as k ranges from N-1 to 1
Since the “square mazes” A2 and B2 of 6b are smaller than C2, either may be placed within it. If B2 is superposed on C2 and its area extracted from it, there is left a “rind” equal to C2 – B2 (figure 6c). From the preceding, we see then that the measure of the rind area is:
A(n-m) = (N – M) + 2 * ∑ k as k ranges from N-1 to M
The condition of Pythagoras — that C2 = A2 + B2 will be shown as satisfied if one can superpose A2 on C2 and exhaust the rind by unwinding the square maze into the same area (6c). This condition is satisfiable for right triangles with sides of integer lengths, but it is hard to see how the approach would apply for triangles with a side of irrational length, such an any isosceles triangle.
More importantly, proving the theorem requires a relation connecting the linear measure of sides with a condition which is true if and only if those sides form a right triangle. Refer to figure 7a. The area of triangle ABC is given by 1/2 the base times the altitude. Given C as the base and height H, the area of ABC is then 1/2 * C * H. That same area is equal to 1/2 * A * B and the height H from C of the triangle equals A * B / C, if and only if ABC is a right triangle. The height H, perpendicular to C, cuts C into two segments L (for large) and S (for small) forming two more right triangles simlar to ABC. Walking along and measuring the lengths of segments C and B and B and L one finds that the ratios of these corresponding sides are equal. Specifically, C is to B as B is to L, and C is to A as A is to S. What does this mean ?
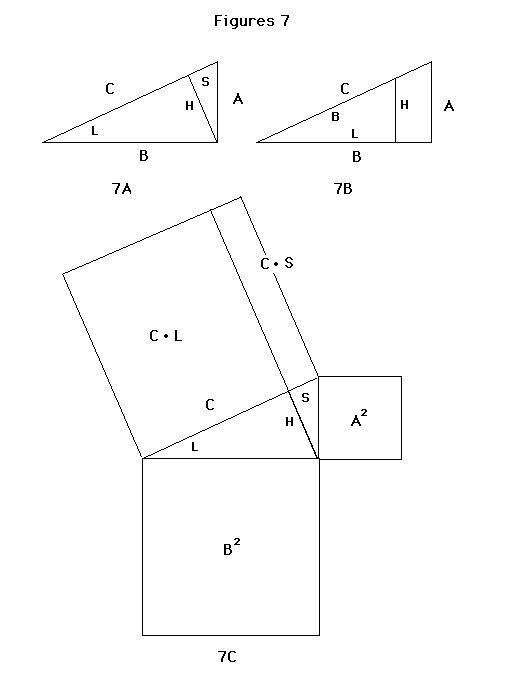
A locomotion-oriented discussion could continue as follows. If we assume ABC to be at the origin of an X-Y coordinate grid (B colinear with the X axis), as in figure 7b, we could set two people walking away from the origin, one along B and one along C, as one might do where angled boulevards cut across the square street grid of a modern city. Under such a scenario, these people would see each other at successive cross streets, perpendicular to B, only if they moved with a common X-component of velocity, Vx. Given that HLB is similar to ABC, HLB could be in imagination rotated out of the plane and reset at the origin with L along the x-axis. The common angle would align B so re-oriented with C also. If H represented another cross street, the same two walkers with constant X-component velocity would see each other as they cross street H after distances L and B respectively. This is one meaning in the assertion that C is to B as B is to l. A second, quite different meaning derives from the following simple transformation:
C / B = B / L by observation (walking about)
C * L = B * B = B2 reorganizing terms (an algebraic move)
If these products are now taken to refer to area (a visually-oriented interpretation), this relation (true only for right triangles) argues that a rectangle constructed of sides C and L would have the same area as a a rectangle constructed of sides B and B (a square), as in 7c. Similarly rectangles of sides C and S and A and A would also have equal areas. Since however, S and L are merely a division of C into line segments, those two rectangles must sum to another of area C * C, whose area thus equals the sums of their separate areas, B * B and A * A. Thus, C2 = A2 + B2 .
Making no claims for either the rigor or elegance of this proof, I ask you to notice, however, that it goes forward with arguments sensible in terms of locomotion until it reaches a critical point: one where a new scheme of representation, a visually oriented one based on static area measures, is introduced to conclude the argument. This particular shift may be required by the theorem itself, whose very power lies in the intricate linking of relations across psychologically varied schemes of representation. That fact may be what made the discovery seem so marvelous in the classical world, worth even the sacrifice of a hundred cows. Further, the required intermodal coordination of schemes presents, as I have argued otherwheres (Lawler 1987), an explanation for the coherence-forming integration of disparate knowledge structures learned through diverse experiences.
I have focused in theses analyses on sensory modal variations of schemes of representations and the possibility of their disparateness and interplay in order to probe our understanding about how the mind constructs itself as a quasi-coherent emergent from the interactions of bits and pieces with which experience begins. The variety of proofs, in terms of mental operations required to follow them, illuminates a central point in the use of multiple representations (now becoming a staple in the design of computer-based learning environments, Kaput, 1988). The flexibility and increased coherence Feynman achieved from his problem-solving practice can be our objective for others if we select representations with mental operations characteristic of the the four primary sensori-motor systems: language, vision, locomotion, and manipulation. A focus on intra-modality translatability, which has long been a desired objective for education practice (witness the “intermodal transfer ” principle in Bauersfeld, 1972) will find its most fecund application through the design of groups of related computer based learning environments whose concrete models cover the same domain and ideas.
Acknowledgments
This paper is an extract from the longer article Shared Models: The Cognitive Equivalent of a Lingua Franca (Artificial Intelligence and Society, Jan. 1989, now republished as chapter 1 of Artificial Intelligence and Education, vol. 2, Ablex, 1992). Many colleagues have contributed substantially to its development, both through critical and constructive conversations. Most recently and importantly, H. Bauersfeld and G. Albers discussed some of the notions presented here. Different modes of mind, as a psychological issue, was raised by S. White; Cellerier’s early musings on the possibilities of various computational primitives for the different modes marked a convergence I considered important. In the background of this work, never very far, are notions absorbed from years of interactions with R. B. Davis, W. Feurzeig, M. Minsky, S. Papert, O.G.Selfridge, and M. Yazdani. An equipment grant from the Apple Education Foundation, a research grant from the National Research Council, and the continuing encouragement of my research liason at the Army Research Institute, J. Psotka, has permitted this work to go forward.
References
Barr, Aaron and Edward Feigenbaum, (eds.) (1981) The Handbook of Artificial Intelligence . Wm. Kaufmann, Inc. Los Altos, Calif.
Batra, Ravi (1987) The Great Depression of 1990 . Dell Publishing, New York, NY.
Bauersfeld, Heinrich. (1972) Einige Bemerkungen zum “Frankfurter Projekt” und zum “alef”-Programm. Materialien zun Mathematikunterricht in der Grundschule . Arbeitskreis Grundschule e. V., Frankfort am Main.
Dawkins, Richard (1976) The Selfish Gene . Oxford University Press. Oxford.
Descartes, René (1954) The Geometry of René Déscartes . Translated by D. E. Smith and M. L. Latham. Dover Publications, New York, NY
Dörner, D. Stäudel, T. and Strohschneider, St. Moro . Projekt “Systemdenken” No. 23. Universität Bamberg.
Drescher, Gary (1988) Demystifying Quantum Mechanics . AI Memo no. 1026. MIT Artificial Intelligence Laboratory, Cambridge, MA.
Feurzeig, Wallace (1987) Algebra Slaves and Agents in a Logo Based Mathematics Curriculum. in Lawler and Yazdani (eds.) Artificial Intelligence and Education, vol. 1 . Ablex, Norwood, NJ
Feynman, Richard (1986) Surely You’re Joking, Mr. Feynman . Simon & Schuster, New York.
Hadamard, Jacques (1945) The Psychology of Invention in the Mathematical Field . Dover Publications, New York, NY
Heath , Thomas L. (1956) Euclid: The Thirteen Books of the Elements (Vol. 1) . Dover Publications, New York, NY.
Held, Richard and Richards, W. (eds.) (1972) Perception: Mechanisms and Models. W.H.Freeman, San Francisco, Calif.
Heppenheimer, Thomas (1977) Colonies in Space . Stackpole Books, Harrisburg, PA
Kagan, Jerome and Havemann, Ernest (eds.) (1968) Psychology: an Introduction . Harcourt, Brace, and World, New York, NY.
Kaput, James (1986) The Role of Reasoning with Intensive Quantites: Preliinary Analyses. Technical Report, Educational Technology Center, Harvard Graduate School of Education.
Langer, Susanne (1953) Feeling and Form . Scribner’s Sons, New York, NY.
Lawler, Robert (1981) The Progressive Contstruction of Mind, Cognitive Science , 5, 1-34.
Lawler, Robert (1985) Computer Experience and Cognitive Development . Ellis Horwood, Chichester, UK.
Lawler, Robert, with Benedict DuBoulay, Martin Hughes, and Hamish MacLeod (1986) Cognition and Computers . Ellis Horwood, Chichester, UK.
Lawler Robert and Gretchen Lawler (1987) Computer Microworlds and Reading: An Analysis for Their Systematic Application in Lawler and Yazdani (eds.) Artificial Intelligence and Education . Ablex, Norwood, NJ.
Lawler, Robert and Oliver G. Selfridge (1985) Learning Strategies through Interaction . Proceedings of the Seventh Annual Conference of the Cognitive Science Society . Irvine, Calif.
Lawler, Robert (1987) Co-adaptation and the development of Cognitive Structures in DuBoulay, Hogg, and Steels (eds.) Advances in Artificial Intelligence . North Holland, Amsterdam.
Lawler, Robert and Masoud Yazdani (1987, 1992) Artificial Intelligence and Education (two volumes). Norwood, New Jersey; Ablex Publishers.
Lietzmann, W. (1911/1953) Der Pythagoreische Lertsatz . B. G. Teubner, Stuttgart.
Minsky, Marvin (1975) A Framework for Representing Knowledge in Winston (ed)The Psychology of Computer Vision. McGraw-Hill, New York, NY
Morgan , Clifford J. (1965) Physiological Psychology . McGraw-Hill, New York, NY
Papert, Seymour (1980) Mindstorms: Children, Computers, and Powerful Ideas . Basic Books, New York, NY.
Peirce, Charles (1878/1956) Deduction, Induction, and Hypothesis in Cohen (ed) Chance, Love, and Logic . Brazillier, New York, NY.
Wertheimer, Max (1959) Productive Thinking . Michael Wertheimer, Ed.. Greenwood Press, Westport, CT.
Publication notes:
Written in 1988.
1989. Published as the beginning of “Shared Models: The Cognitive Equivalent of a Lingua Franca,” in Artificial Intelligence and Society, Elsevier.
1991. Republished in Artificial Intelligence and Education, V.2. (Ablex, 1996)
1996. Republished in the Journal for Mathematical Behavior (Ablex, 1996).
