The Progressive Construction of Mind
“Pas de genese sans structures; pas de structures sans genese.”
J. Piaget
Studying Natural Learning
We follow Piaget’s abstruse paradox (“There can be no development without structures nor any structures without development”), arguing by example that one can understand learning with structural conceptions and that one can understand cognitive structures in detail by tracing their development. Focusing on changes in the organization of distinct and separate cognitive structures, we explain some significant learning as enhancements of performance which emerge from small changes in that organization.
The Intimate Study
We tried to trace the path of natural learning in a project I named “The Intimate Study”. The attempt was suggested in part by Flavell’s (l963) pointing to “…a research endeavor which has not yet been exploited: an ecological study of the young child’s mundane interchanges with his workaday world….” and was consonant with Neisser’s (l976) call for ecological validity in psychological experiments.
The subjects, my two children Robby and Miriam, were mainly in my care. Miriam turned six as the study began and entered first grade at its end. Robby’s eighth birthday came during the study. They were out of school; friends were gone for the summer. Rather than my being merely their shepherd for a while, we three agreed to engage in a research project at my laboratory. The children were less subjects of my experiment than colleagues. The project was not confined to the laboratory but came home with us to the heart of my family. The six months of The Intimate Study (April through September, 1977) created an extensive and detailed corpus of observations. There were 67 sessions at the MIT Logo laboratory and 24 at home; these were typically 30 to 60 minutes in length. All were recorded on audio tape and many on video tape. All the recorded material that relates to Miriam’s work in these sessions has been manually transcribed; such is the basic corpus.
A hundred thirty “vignettes” extend the corpus. These documents of naturalistic observation — think of them as short stories of three to four pages — attempt to capture what the children were doing and learning outside the laboratory. The study included pre and post testing — many of the tests were derived from the experimental tradition of Piaget. (Most are not directly relevant to the specific topic of this article.) The Intimate Study has been further supplemented by recollection and observations of Miriam’s years the project and her subsequent development.
The Particularity of Knowledge
Our focus on the particularity of knowledge exhibits a primary stance of this research. We hope to avoid abstractions and the process of “abstraction” by describing the emergence of broadly applicable skills from the interaction of highly particular knowledge. This objective was a basic motive for constructing so detailed a corpus. The corpus is reasonably complete with respect to calculation, by which I mean the following. The manual transcription of all Miriam’s mechanically recorded formal sessions has permitted subsequent easy access for analysis and interpretation. Mechanical reproduction has remained useful where specific questions of a fine grain needed to be resolved.
Beyond the range of mechanical recording, three elements of our situation contributed to the completeness of the material. First, we lived on a relatively isolated suburban estate, spacious enough for the children to play but remote from other contacts and entirely within my purview. I kept, more or less regularly, an hourly log of short notes about Miriam’s activities. Finally, Miriam took such pride in her developing knowledge of calculation that she was eager to discuss with me her latest speculations — thus her covert calculations were also brought, albeit imperfectly, to my notice.
Learning about Learning about Something
From this corpus, I have extracted the following story of Miriam’s learning to add and on it erected an interpretation of how that learning happened. Figure 1 presents as a guide for the reader a chronology of calculations cited and the main insights Miriam experienced on her path to mastery of addition. Because the case material presented here deals with simple arithmetic, a reader might believe that our theme is “addition”. Such is too limited a view. Our theme is learning but, if I may paraphrase Papert, “You can’t learn about learning; you can only learn about learning something.” How to add is one of the “somethings” which we observed this child master in our attempts to learn about learning.

The Organization Of Disparate Structures
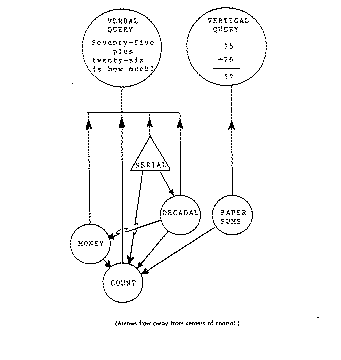
My commitment is to explore how disparate, i.e. separate and distinct, structures of knowledge interact and become integrated. What are the phenomena that argue there is such disparateness of related cognitive structures ? The following example, which I offer to represent the general case, is based on material from late in the study and shows three different solutions to the “same” problem. I asked Miriam, “How much is seventy-five plus twenty-six ?” She answered, “Seventy, ninety, ninety-six, ninety-seven, ninety-eight, ninety-nine, one hundred, one-oh-one [counting up the last five numbers on her fingers].” I continued immediately, “How much is seventy-five cents and twenty-six ?” She replied, “That’s three quarters, four and a penny, a dollar one.” Presented later with the same problem as a paper sum in the vertical form of addition, she would have added right to left with carries.
Three different structures apparently could operate on the same problem. The evidence about the disparateness of structures is that Miriam did not, in fact, apply the result of the first calculation to the second formulation of the problem. Moreover, for a long time she did not relate paper sums to mental calculation at all. We may infer, further, that structures differ in their analysis of what the significant parts of the problem are and how those parts are manipulated to reach a solution. One structure analyzes the problem in terms of multiples of ten and counting numbers. Another deals with coin denominations and known equivalences. The third deals with the columns of digits and their interactions. Ginsberg (1977), in dwelling on the “gap”between children’s formal and informal knowledge of arithmetic, witnesses that the disparateness of knowledge is more common than rare. Finally, observing that how a problem is presented affects which specific structure engages the problem confirms the disparateness of cognitive structures in general.
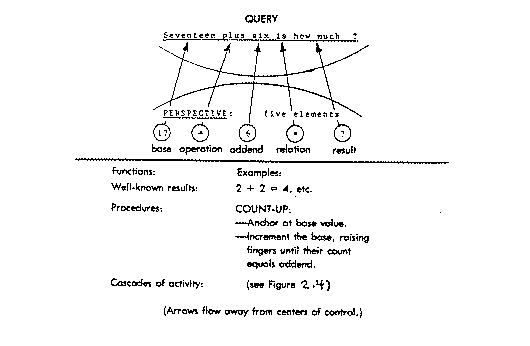
In answer to the particular problem of Figure 2, which I posed in the initial test of Miriam’s calculation skills, she said, “Well, seventeen [then finger counting by the value of the second addend], eighteen, nineteen, twenty, twenty-one, twenty-two, twenty-three. Twenty-three is the answer.” This counting knowledge was limited in scope, so although Miriam might add 89 plus 7 by finger counting, she couldn’t add 89 plus l4. Her occasional use of hash marks — vertical strokes drawn on a piece of paper — instead of fingers to work out sums beyond ten testifies to the firm rootedness of this knowledge in one-to-one correspondence. (In arguing with her brother about a large sum, before the beginning of The Intimate Study, Miriam represented an addend by drawing hash marks on a paper napkin.)
A New World Of Experience
If some knowledge comes from experience, new experiences bear special scrutiny for the role they have in engendering new knowledge. One significant new element in The Intimate Study was Miriam’s engagement with Logo language computer systems. Most of our working sessions occurred at M.I.T.’s Logo Project. Many involved play with computer systems using the Logo language. The central activity through which children have been introduced to Logo is “turtle geometry”. That children’s mathematical world is a geometry of action. The child specifies commands, e.g. “move forward some distance” or “turn right through some angle,” for execution by a computer-driven agent, known as the “turtle.” The turtle exists in two forms: a small floor robot and a triangular cursor on a video display. The turtle is equipped with a pen which will, on command, draw a line as the turtle moves from one place to another. The commands of movement, rotation, and pen control provide a drawing tool — one significantly different from children’s other experiences because of the pervasive quantification required by the use of the turtle commands.
The Specialness of 90 Degrees
The specialness of 90 (as the number of degrees in a right angle) was unrecognized by Miriam early in The Intimate Study. For example, when directed in a game by her brother Robby (age 7 years, 10 months — 7;10) to turn “right 90,” Miriam (at age six years, 1 month — 6;1) turned her right foot about 60 degrees, brought her left to it and said “one.” She repeated the action and counted with each “two…three..four…” etc. Robby gave her instruction in what “right 90” means: “look straight ahead and hold your arm out at your side; jump right around so your feet point where your arm is pointing.”
The specific knowledge of what right 90 means and that two executions of right 90 are required to turn around are needed to make line-drawings in turtle geometry. When used in solving particular problems later, this specific result, 90 plus 90 equals 180, is a sign that Miriam’s knowledge rooted in turtle geometry was implicated because that result was well known to her before she knew that 9 plus 9 equals 18. For example, at six and a half, Miriam mentally calculated 96 plus 96, using 90 plus 90 = 180, while days later she still calculated 9 plus 9 by deforming it to 8 plus 8 plus 2.
Pervasive Quantification
The pervasive quantification of computer experience is evident in Miriam’s early play with her favorite computer game, SHOOT. In Figure 3, the square boundary represents the computer video display, the circle is a target, and the triangle is the turtle. The objective of the game is to get the turtle into the target using the Logo turn commands to aim and a SHOOT procedure to move the turtle forward into the target. A point is scored when the turtle lands in the target. Should the turtle miss (for example, by going too far as in Figure 3), a trace is left on the video display and after a short time, the turtle returns to its initial location and orientation.
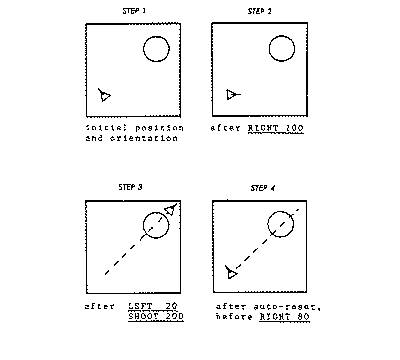
In the incident depicted in Figure 3 (around 6;1), Miriam first commanded “right 100.” She judged the turtle had turned too far and compensated with a “left 20.” The command “SHOOT 200” took the turtle beyond the target, so it returned to its initial state. Miriam’s next command, “right 80,” shows she compacted the two earlier turning commands to a single one. This required her mental calculation with the decades(100 and 20); I call such multiples of ten decadal numbers.
Frequent play with SHOOT involved her in performing mental calculation with such decadal numbers at nearly every turn. She did not indulge in mental calculation for its own sake; it was a subordinate task rendered meaningful by being embedded in a activity she enjoyed for a variety of other reasons.
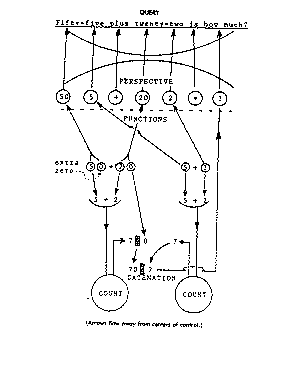
Let’s suppose that from playing with SHOOT and the experience of computer drawing Miriam was developing a new microview. Let’s call this the DECADAL MICROVIEW because a primary characteristic of its activity was the mental calculation of sums using decadal numbers. Consider a typical calculation problem in this Decadal microview, “55 plus 22 is how much ?” (This might arise where Miriam first turned 55 degrees then decided to turn further, 22 degrees.) The perspective exhibited in Figure 4 analyzes the problem as she formulated it into elements; then a set of functions execute. First, the fifty and twenty are grouped, then stripped of their zeroes. The modified symbols (i.e.,”5″ and”2′) are passed to the Count view from which a result, “7”, is returned. By restoration of one zero, the”7″ is reconstituted to ’70”, a number of the right order of magnitude. Similarly, the five and two are added by invocation of the Count microview knowledge. The two partial results are catenated to produce the answer, an operand value, which Miriam then used in the Logo command. The claim implicit in this interpretation is that catenation of separately achieved partial sums — both separately performed by the Count microview — was the key function of the Decadal microview.
Three Bits of Evidence
What evidence is there that the invocation of the Count view was involved in calculating such results ? Three kinds. First, Miriam’s repertoire of well-known results did not include these decadal numbers. Second, during calculations such as “50 plus 20″, I often witnessed Miriam counting on her fingers. Finally, Miriam’s guessing pattern indicated she was manipulating symbols without fully understanding their significance. Consider this detailed example. To add the numbers”50″ and”20″ on one’s fingers requires deforming the terms to other representable analogs,”5″ and”2″, by stripping off two zeroes. To reconstitute the Count view results for use in Decadal, a single zero is catenated with”7″ to make”70”.
The other zero remains unused, stripped off and not later reaffixed; this is the “extra zero problem,” which caused frequent confusion as we see in the following. Adding 97 plus 64, Miriam separated the decades, added, and guessed, “That is 15 tens….500 ?” Whatever the actual representation in Miriam’s mind, such guesses show there was a second zero to which she was sensitive, whose non-representation in the result she couldn’t account for; I take that as further evidence calculations proceeded as described.
Genesis And Structure
The evidence for the manner in which the Decadal perspective analyzes a problem to elements is based on the interpretation of an incident where this new structure came into being, a moment of insight, and on a knowledge of the Decadal view’s predecessors. The moment of insight occurred at Miriam’s age 6;0;26 while the children were playing with SHOOT. Miriam’s older brother Robby demanded his turn — they were fighting over who would use the terminal — and Miriam ended up with the piano. She played the piano with her elbows while they argued about how much to turn the turtle; the numbers 50 and 53 were mentioned frequently. In this midst of this chaotic scene, Miriam inquired of Robby, “How much is fifty plus fifty-three ?”
How could Miriam NOT know such a result ? Is it not likely she knew fifty cents plus fifty three made up a dollar three ? It could very well be. The point is that Money view knowledge does not imply the existence of cognate Count view knowledge. Further, the ability to add on a small addend to a counting number name does not imply that such a number name as fifty three could be analyzed into parts which could then be recombined after operations had been performed on them. More generally, the claim for the disparateness of microviews means we should not assume the existence of knowledge applicable in one task domain applies anywhere else. The functions of such microviews are only locally applicable. What is known by microviews has a very limited lawfulness, rather like Hooke’s “Law of Elasticity” which is defined as applying over that range to which it applies.
Robby answered Miriam’s question, “A hundred and three.” I take the QUESTION as evidence that Miriam did not know the answer and interpret it as a request for a specific result. Robby’s answer brought with it an insight — that in the world of turtle geometry fifties can be added together and a unit cut off from one can be subsequently re-affixed by a simple catenation of number names. Miriam confirmed her insight a moment later by asking, “What is fifty-three plus fifty-three ?” She answered the question immediately herself, “A hundred six.” To appreciate her insight into the legitimacy of catenating decadal and unitary number names in a context of addition operations we must relate the incident to Miriam’s antecedent microviews of Money and Count.
The Money view
The Money view had its roots in Count, but it involved counting with a difference: denominations in coin values. Pennies, nickels, dimes, quarters, halves, dollars — these were the elemental things of Miriam’s Money microview. The procedures were more complicated and various than those of Count. For example, Miriam would calculate her allowance (a nickel for each year of her age) by skip-counting (5, 10, 15, 20, etc.) under finger-counting control: each finger raised represented one year of her age. The well-known results of the Money view were highly particular. Miriam knew that 15 cents plus 15 cents was 30 cents because each five-pack of her favorite gum cost 15 cents and she knew she could buy two of them with her allowance. Similarly, the elements of denomination each involved some few well known results, e.g., 2, 3, and 4 quarters were 50 cents, 75 cents, and a dollar. Miriam also knew around age six some decadal sums from counting dimes, but there is no indication of extensive systematic knowledge of dime-based calculations. The perspective of the Money view superposed the denominations of coins on the countable objects of the Count view’s perspective. Its knowledge comprised a specialization of the Count microview perspective, extended in particular directions because of the accidents of the American coinage and Miriam’s spending habits. Even though its genesis occurred before the beginning of The Intimate Study, we can describe with confidence the Money view as an experience-elaborated DESCENDENT of the ANCESTRAL Count view. The implication of this descent of one microview from predecessors is that the ancestral perspectives provide the initial structures for the elements of the descendent’s perspective. That is, “what’s what” in a microview begins with its likeness to what was recognizable in ancestral views and proceeds through further differentiations based on the lessons experienced in a particular environment.
The Control Structure Of Mind Embodies The Genetic Path Of Learning
The perspective of the Decadal view embodies a specialization of the idea of denomination first introduced with the Money view. It is a specialization in the sense that the two significant denominations are tens and ones. Decadal is a descendent of the Money microview. The application of the denomination idea to the decadal numbers representing angles in turtle geometry changed the elements to which the idea was applied from concrete objects, such as coins, to symbolic objects, i.e. to digits and names for large numbers of uncertain significance. The insight that the number names, used for counting as well as turtle geometry, could be separated as decades and units for addition, then recombined by catenation is, by itself, provide evidence that Decadal was closely related to Count, as well. The frequently repeated advice that she should consider Decadal sums as analagous to the well known results of the Count view demands that we describe Decadal as descended from Count as well as from the Money view. This common descent from two ancestors will be represented in Figure 5 (discussed in the section Coordinating and Task-rooted Structures) by the channels of communication through which the Decadal view may invoke results of both ancestors. That is, The Control Structure of Mind Embodies The Genetic Path of Learning.
The Introduction Of Paper Sums
The Intimate Study began with Miriam unable to add 10 plus 20 as a paper sum in the vertical form. When I posed verbally the question “How much is ten plus twenty ?”, Miriam answered with confidence, “Thirty”. Her response to the first sum below (a) was quite different. “I don’t know… twelve hundred ?” (After this confusion, vertical lines were used frequently to emphasize column alignment.):
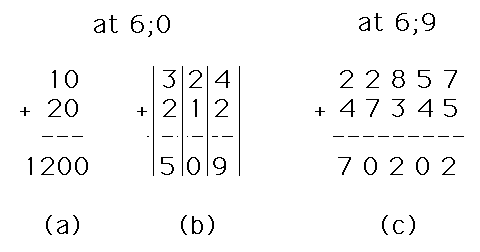
Despite instruction that she should not “read” the individual digits but should add within the columns and assemble a result from the columnar sums, Miriam added the addends to “five hundred nine” for sum (b) [2+1+4+2 = 9]. We continued to use the vertical lines shown above to emphasize the column divisions. She received instruction for solving problems such as (c) by a procedure I call “order-free adding” — one based on the very simple idea that it doesn’t matter in what order one sums column digits so long as any column interaction is accounted for subsequently.
There were many single-digit sums which Miriam did not own as well-known results and would calculate on her fingers, such as”8 plus 3.” After preliminary instruction, the typical problem Miriam confronted in order-free adding presented two multi-digit addends in the vertical form. Her typical solution began with writing down from left to right the well known results of column sums. Next, Miriam would return to the omitted subproblems and calculate them with her fingers. When this first pass solution produced multi-digit sums in a column — a formal illegality, as I informed her — Miriam had to confront the interaction of columns. I instructed her to cross off the ten’s digit of such a sum and add it as a 1 to the next left column, that is, to “carry the one.” With less than two hours of such instruction, Miriam succeeded at solving sums with two addends of up to ten digits; but she realized no significant gain, for the procedures were subject first to confusion and then to forgetting.
Confusion and Vulnerability
Why were Miriam’s initial skills with paper sums vulnerable? Consider the three representative solutions below:
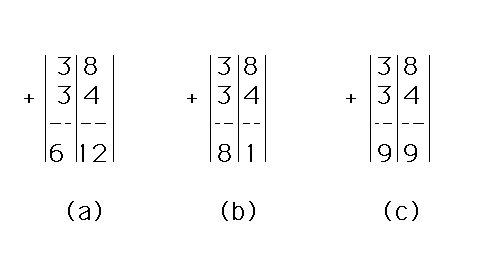
The first (a) shows no integration of columnar sums; the second (b) shows a confusion over which digit to “put down” and which to “carry” (with an implicit rule-like slogan behind the action). The third (c), a conservation response, is an invention of Miriam’s which will be described more fully below. If you don’t already understand the meaning of the rule “put down the N and carry the one,” why should you prefer that to a comparable rule, “put down the 1 and carry the N” [as in (b) above]. Miriam was confusable in the sense that she chose, with no regularity and no apparent reason, to apply both these rules. Although frequently instructed in the former rule, she did not remember it. The rule-like formulation made no direct contact with her underlying microview structures. Without support from “below,” the rule could not be remembered. Miriam eliminated her confusion, by inventing a carrying procedure that made sense to her, shown in (c) above. “Reduction to nines” satisfied the formal constraint that each column could have only a single digit in the result by “reducing” to a “9” any multi-digit column sum and “carrying” the “excess” to the next left column. (38 plus 34 became 99 through 12 reducing to a 9 with a 3 carried, i.e. added to the two threes of the ten’s place.) Miriam’s invention of this non-standard procedure (at 6;3;6) I take as weighty evidence characterizing her understanding of numbers and addition in the vertical form. (The latter we will discuss shortly.) About numbers we may conclude she saw the digits as representing things which ought to be conserved, as did the numbers of the Count microview. The achievement of columnar sums by finger counting or by recall of well-known results further substantiates the relation of paper sums to numbers of the Count view. Let us declare, then, that these experiences led to the development of a cognitive structure, the PAPER-SUMS microview, a direct descendent of the Count view.
Correctness is a Local Judgment
Miriam did not understand “carrying” as being at all related to place value. The numbers within the vertical columns did not relate to those of any other column in a comprehensible way. Despite my initial criticism of “reduction to nines” — by asking if she were surprised or not that all her answers had so many nines in them — Miriam was strongly committed to this method of carrying. For Miriam, at this time, addition in the vertical form had nothing to do with the Money or Decadal sums she achieved through mental calculation. “Right” or “wrong” was a judgment applicable to a calculation only in the terms of the microview wherein it was going forward. I conclude then that the Paper-sums microview shows a diverging line of descent from Miriam’s counting knowledge, diverging with respect to those other microviews which involved mental calculation.
Confusion, Interference, and Forgetting
The more general final point is that what “made sense” to Miriam completely dominated what she was told. She could not remember a rule with arbitrary elements, an incomprehensible specification of what to put down and what to carry. Why is it that a rule “put down the N and carry the 1” didn’t make sense ? How can we recapture a sense of what that must have seemed like ? To her, a number represented a collection of things with a name: “12” was a name by which reference could be made to a collection of twelve things. Numbers may have seemed to her as words do to us, things which cannot be decomposed without destroying their signification. If you divide the word “goat” into “go” and “at,” you have two other words not sensibly related to the vanished goat. Similarly, from our common perspective, if you don’t see the”1″ as a”10″ when you decompose a”12″ into a”1″ and”2″, you lose”9″. Unless you appreciate the structured representation, the decomposition of 12 can make no more sense than cutting up a word. What appears as forgetting in Miriam’s case is an interference of equilibration processes; that is, what makes sense in terms of ancestral cognitive structures dominates what is inculcated as an extrinsic rule. (I don’t claim here to offer a theory of forgetting. Competition from sensible ideas of long dependability is a very good reason, however, for forgetting what you’re told but can’t comprehend.)
The Carrying Breakthrough
The “carrying problem” was not restricted to Paper-sums and was, in fact, first resolved among the micro views of mental calculation. Although she could add double digit numbers that involved no decade boundary crossing, like 55 plus 22, Miriam’s Decadal view functions failed with sums only slightly different, such as 55 plus 26. Sums of this latter sort initially produced results with illegal number names, i.e. 55 + 26 = 70:11
(“seventy-eleven”). In playing with SHOOT, however, precision was not required. Miriam’s typical “fix” for this problem was to drop one of the unit digits from the problem and conclude that 55 + 26 = 76 was an adequate solution. She could, of course, cross decade boundaries by counting, but for a long time this Count view knowledge was not used in conjunction with her Decadal view knowledge. Miriam’s resolution of one carrying problem became evident to me in her spontaneous presentation of a problem and its solution (at 6;3;23). She picked up some of her brother’s second grade homework and brought it to me:
Miriam: Dad, twenty eight plus forty eight is seventy six, right ?
Bob: How did you figure that out ?
Miriam: Well, twenty and forty are like two and four. That six is like sixty. We take the eight, sixty-eight (and then counting on her fingers) sixty-nine, seventy, seventy-one, seventy-two, seventy-three, seventy-four, seventy-five, seventy-six.
Here was clear evidence that Miriam had solved one carrying problem by relating her Decadal and Count microviews. When and how did that integration occur ?
A Moment of Insight
The corpus of The Intimate Study is sufficiently rich in detail that I have been able to trace to a moment of insight Miriam’s integration of formerly disparate microviews. We were on vacation at the time. I felt Miriam had been working too hard at the laboratory and was determined that she should have a rest from our experiments. I was curious, however, about the representation development of her finger counting and raised the question one day at lunch (at 6;3;16):
Bob: Miriam, do you remember when you used to count on your fingers
all the time ? How would you do a sum like seven plus two ?
Miriam: Nine.
Bob: I know you know the answer — but can you tell me how you used
to figure it out, before you knew?
Miriam: (Counting up on fingers) Seven, eight, nine.
Bob: Think back even further, to long ago, to last year.
Miriam: (Miriam counted to nine with both addends on her fingers — leaving
the middle finger of her right hand depressed.) But I don’t do that any more.
Why don’t you give me a harder problem?
Bob: Thirty seven plus twelve.
Miriam: (With a shocked look on her face) That’s forty-nine.
Something about this problem and result surprised Miriam. I recorded this situation and her reaction in a Vignette; I did not appreciate it as especially significant at that time. My current interpretation focuses on this specific incident as a moment of insight.
The Method of Ascription
It is the rich corpus of The Intimate Study, conjoined with its detailed analysis, that permits me to ascribe with confidence a particular change in cognitive structure to a specific situation. When such a status is assigned to an incident, the moment of insight can be judged as significant only in the context of an interpretation. Here is an abstract of the methodology. Notice through behavior evidence of two different states of cognitive structure. For example, Miriam was able to sum 48 plus 28 where previously she had dropped one of the unit’s digits in such a problem. Proceed in the detailed analysis of the corpus (i.e. the examination of every item of overt behavior possibly related to the state change) to determine in what situations and how rapidly the change of state became manifest. When a moment of insight is assigned to an incident, such as the finger counting incident above, reexamine the corpus for conflicting or supporting evidence. One hopes, with a final interpretation, to find only supporting evidence, as the following. During the remainder of our vacation, Miriam pestered me to do some addition experiments. I tried to give her a rest, and her pestering intensified. As we drove back from our vacation, she made me promise to do an experiment as soon as we reached home: that day she brought to me the problem of 28 plus 48 described above. Miriam clearly owned some new knowledge she wanted to employ.
Characterizing the source of an Insight: a surprising confluence of results
How should one characterize this insight ? Precisely what was it that Miriam saw ? In the Decadal view, the problem “thirty-seven plus twelve” would be solved thus, “thirty plus ten is forty; seven plus two is nine; forty nine.” The Decadal view would have produced a perfect result. Miriam had recently become able to decompose numbers such as “twelve” into a “ten” and a “two”. This marked a refinement of the Count view perspective. If we imagine the calculation “thirty seven plus twelve” proceeding in the Count microview — with the modified perspective able to “see the ten in the twelve” — Miriam would say “thirty seven [the first number of the Count view’s perspective], plus ten is forty seven [then counting up on her fingers the second addend residuum], forty eight, forty nine”. Such a Count view calculation also yields a perfect answer. We are not surprised that the answer is the same as that of the Decadal view, but I believe the concurrence surprised Miriam. One can say that Miriam experienced an insight (to which her “shocked look” testifies) based on the SURPRISING CONFLUENCE OF RESULTS from apparently disparate microviews.”Insight” is the appropriate common word for the situation, and I will continue to use it where no confusion is likely; but its range of common usage extends so far as to prohibit its technical use. So I introduce a new name, the elevation of control, as the technical name for the learning process exemplified here. The ELEVATION OF CONTROL names the creation of a new control element which subordinates previously independent microviews, in the sense of permitting their controlled invocation; some experiences of insight are the experienced correlates of control elevation.
Characterizing the Elevation of Control
The character of control elevation is revealed in the example. The numbers thirty-seven and twelve were of such a magnitude as would have normally engaged Miriam’s Decadal microview. She had just been finger counting (a Count view function) and Decadal could calculate the sum as well. If both microviews were actively calculating results and simultaneously achieving identical solutions, the surprising confluence of results — where none should have been expected — could spark a significant cognitive event: the changing of a non-relation into a relation, which is the quintessential alteration required for the creation of new structure.
[note 1]
The sense of surprise attending the elevation of control is a direct consequence of a common result being found where none was expected. The competition of microviews, which usually leads to the dominance of one and the suppression of others, also presents the possibility of cooperation replacing competition. So we see, in the outcome, Decadal begining a calculation and Count completing it. This conclusion, howevermuch it is based on a rich interpretation, is an empirical observation. Where we expected development in response to incrementally more challenging problems, we found this form of insight: cognitive reorganization from the redundant solution of simple problems.
Coordinating And Task-Rooted Structures
The elevation of control, a minimal change which could account for the integration of microviews witnessed by Miriam’s behavior, would be the addition of a control element permitting the serial invocation of the Decadal view and then the Count view. Let us declare at this moment of insight the formation of a new microview, the SERIAL view [note 1]. The perspective of the Serial view analyzes a problem into a “part-for-Decadal” and a “residuum.” 28 plus 48 would be regrouped as a part for Decadal (28 plus 40) and a residuum (8). The functions of this view first invoke Decadal; upon return of the Decadal partial result, they invoke Count to complete the sum.
Structurally, the Serial view is similar to its predecessors, but functionally and genetically it is quite different. Microviews whose perspective elements are descriptions of things, speculations about the relations of which may be verified or disconfirmed by straight-forward experiments, are TASK-ROOTED. We may note that the Count view is rooted in one-to-one correspondence, the Money view is committed to a coinage-rooted perspective, and the Decadal view handles problems of a magnitude encountered in the scale of angles. These three are task-rooted structures (and the Paper-sums view is another). The knowledge which such views constitute is constructed through experience by elemental description refinement on a perspective descended from an ancestral view. The well-known results of such task-rooted views may be determined by accident, as Miriam’s knowing that 15 cents plus 15 cents sums to 30 cents derived from the price of gum and the amount of her allowance. Other results are less accidental. That is, Miriam knew 90 plus 90 equals 180 because this sum (whose quantity and representation are cultural accidents) embodied a significant action (turning around) in worlds of experience. We can state the observation more generally this way: the particular knowledge of a microview may be accidentally determined, but the microviews themselves are not accidental; they come to embody what is epistemologically profound in the experiences which inspire their construction. I return to this point in the penultimate paragraph of the chapter.
The Serial view is not a task-rooted microview and is different from such a one in several ways. Recall that task-rooted microviews may have merely a single ancestor, as the Money view’s sole ancestor is Count. Microviews such as Serial which coordinate others must have at least two ancestors. Further, the elements of the Serial view’s perspective are not descriptions of things in the world of common experience but are descriptions of the perspectives of the coordinated microviews. The Serial view functions by invoking the subordinated microviews and not by recall of locally well-known results or execution of local procedures. Whereas the generation of the task-rooted views involves both insights about what are the significant elements of microviews and progressive familiarization with what can be done to them, the Serial view is so simple as to be complete at its inception. Finally, the problem confronted at the moment of insight (37 plus 12) did NOT require the insight to solve it. In this specific sense, the cognitive development was “accidental” as opposed to being experience driven. In a second sense, it was not accidental at all, for it depended upon the simultaneous engagement of robust ancestral knowledges. I will return to this issue at the end of this chapter.
Emergence of a New Functional Level of Calculation Ability
Although the Serial view is achieved as a minimal change of structure, its integration of subordinated microviews permitted a significantly enhanced calculation performance, one so striking as to support the observation that a new functional level of calculation emerged from the new organization. This is especially evident where knowledge is articulated by proof. Consider this example (at 6;5;24). Miriam and Robby, himself no slouch at calculation, were making a clay by mixing flour, salt, and water. They mixed the material, kneaded it, and folded it over. Robby kept count of his foldings. With 95 plies, the material was thick. He folded again, “96,” then cutting the pile in half, flopped the second on top of the first and said, “Now I’ve got 96 plus 96”. Miriam interjected, “That’s a hundred ninety two.” Robby was astounded, couldn’t believe her result, and called to his mother to find if Miriam could possibly be right. Miriam responded first, “Robby, we know ninety plus ninety is a hundred and eighty. Six makes a hundred eighty six. [Then counting on her fingers] One eighty-seven, one eighty-eight, one eighty-nine, one ninety, one ninety-one, one ninety-two.”
We can see the Decadal well-known-result (90 plus 90) as a basis for this calculation and its relation to her counting knowledge. Both these points support the argument that Miriam’s new knowledge was specifically of controlling pre-existing microviews. Robby was astounded — and we too should try to preserve a sense of astonishment in order to remain sensitive to how small a structural change permits the emergence of a new level of performance.
The advent of the Serial view marks the furthest reach of Miriam’s mental calculation skills during The Intimate Study. Figure 5 summarizes the development of the mental calculation cluster of microviews. The genetic structure, the descent of a microview from its ancestors, is preserved in the functioning control structure of the mind. Task-rooted and control microviews compete among themselves in a race for solution, a race open to bias by the presentation of the problem, and they invoke the knowledge of ancestral microviews where appropriate. (Such is conceivable even when an invoked ancestor is simultaneously a competitor.) The structure is of a mixed form, basically competitive but hierarchical at need. This vision of mind, the system of cognitive structures, presents disparate microviews of knowledge based on particular experiences. The elevation of control acts to integrate the disparate microviews. Most striking is the observation that the moment of insight resulted from solving a problem for which either of two competing microviews was adequate. That is, the elevation of control was NOT necessity driven but rather derived from the surprising confluence of results where no such agreement between disparate structures was expected.
Paper Sums And Mental Arithmetic
The core of The Intimate Study came to an end without Miriam’s having learned to add, in the narrow sense of using the standard algorithm in the vertical form, but she did learn to do so subsequently. In the intervening months, she returned to school (first grade) and confronted these typical calculation problems: 2 + 3 = [ ]; if John had 7 cents and bought a nickel candy, how much would he have left ? When a severe winter storm kept us snow bound for a week, we extended The Intimate Study (around 6;9) for those days with several experiments during which Miriam learned to add, in the narrow sense.
The objective of these late sessions was to lead Miriam to a vision of carrying as making sense in terms of her appreciation of the representation. In the midst of one session, I posed the problem “how much is 14 plus 27 ?” by writing in the vertical form (a). Miriam calculated the answer mentally and wrote “41” on the chalkboard. I continued, “I want you to look at the problem a different way (writing 10 + 4 and 20 + 7) (b). Can you see the 10 in the 14 ? Can you see that 10 plus 4 is 14 ?” Miriam responded, “Sure,” and writing “= 14” and “= 27” she concluded, “and the answer is 41; we did that already.” I tried a different tactic:
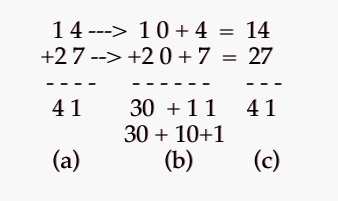
Bob: Now how much is the ten plus twenty ?
Miriam: Thirty.
Bob: [writes”30 +” in the answer line of (b).]
Miriam: Plus…Oh [tapping”4″ first then”7′] seven and
four.
Bob: How much is that ?
(1) Miriam: Thirty-seven [then using her fingers] thirty-eight,
thirty-nine,
forty, forty-one. [Points to the answer
in (a).]”41.’
Bob: How much is seven and four ?
Miriam: (Pause) Eleven.
Bob: Will you write down the”11″ ?
Miriam: (She does so.) Eleven.
Bob: Is there a ten in the eleven ?
Miriam: Yes. Equals forty-one [writing”41″ in (c).].
Bob: What you have to see, Miriam, is that the eleven
there
is a ten plus a one. [writes”10 + 1′
under”11″ in (b).]
Miriam: Yeah ?
Bob: And whenever you get a ten in something like an
eleven or fourteen,
you have to add it with the
thirties [writes a second”30 +” before the
“10 + 1” in (b).]
Miriam: Why not the twenties ?
(2) Bob: So thirty plus ten —
Miriam: (Interrupting) Is forty.
Bob: And then plus one —
Miriam: (interrupting) Is forty-one.
Bob: Does that make sense now ?
Miriam: Yeah.
Bob: Does it really make sense, or are you just
humoring me ?
Miriam: I tell you it really makes sense.
In the dialogue cited (transcribed from videotape), Miriam’s Serial view knowledge was active at (1) above on the distributed form of the problem (b) to arrive at the result she already knew to be correct. After my pointing to the “ten in the eleven” at (2) above, Miriam could see that the results of vertical form calculations could be the same as those of mental calculations. This amounted to an insight that the Paper-sums view related to the Serial view in a significant way.
On First Seeing the Meaning of Place Value in Addition
After I set down the next problem [see (a) below], Miriam’s Serial view knowledge produced the result”93″. Congratulating her for a correct result, I erased her answer, drew in the columnar division lines of (b) and asked her to calculate the result differently. She wrote an”8″ in the ten’s column, scratched it out and wrote in”93″. I stopped this attempt to bypass the problem, wrote an”8″ and a”13″ in the answer line of (b) and asked:
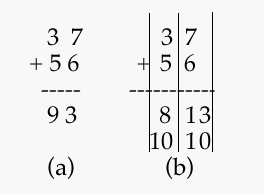
Bob: Can you tell me why this [the”8″ and”13′]
makes sense ?
Miriam: It makes sense because there’s a ten (writing”10′
under”13′);
plus three is in the thirteen.
Bob: I’ll buy that.
(1) Miriam: And if there’s a ten, you add it to the eighty.
Bob: And what do you get ?
(2) Miriam: [Tapping the”3″ of the ten’s column in (b).]
Is this a thirty ?
Bob: Yeah !
Miriam: [Writes a zero to the right of”8″ in the ten’s
answer cell of (b).]
Plus ten is ninety-three,
and the answer’s ninety-three.
At point (2) in the citation above, Miriam asked me, for the first time, about the place value of a digit. This is the moment where she had an insight into the nature of the representation which permitted her thereafter to do addition problems in the vertical form. Seeing that the”3″ was really a”30,” she transformed the”8″ to an”80″, to which it made sense to add the”10″ of”13″. (I interpret the “eighty” of statement (1) above to be the intermediate result, “eighty,” of the Serial micro view calculation. Notice that Miriam appended the”0″ to the”8″ only after establishing that the “3” was a “30.”)
The Correlation of Perspectives
During the core of The Intimate Study, Miriam’s Paper-sums knowledge was so remote from her knowledge of mental calculation that she did not imagine results of cognate problems should be the same. In the preceding incidents we have seen Miriam making sense of the Hindu-Arabic representation — as that intersects with the standard addition algorithm — by connecting it coherently with her dependable knowledge of mental calculation. Figure 6 names CONFORMAL the structural element connecting the Paper-sums view to the views of mental calculation. The implication of the name is that the knowledge of the Conformal view is a mapping, a set of correspondences between aspects of some calculation views and others. Which views ? Which aspects? The most significant insight was that the “3” of “37” was really a “30” as is the “thirty” of “thirty-seven.” This is a part-to-part correspondence of elements in the perspectives of both the Paper-sums view and the mental calculation views. If we pursue the question, “Which views ?”, we must conclude the description of the place value of Paper-sums columns relates to perspective elements of the Decadal view while the coherence of results relates the Paper-sums and Serial views.
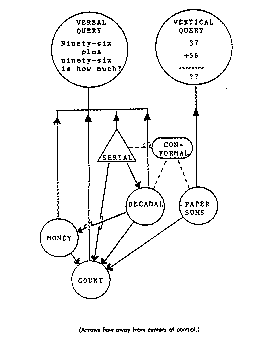
From the CORRELATION OF PERSPECTIVES, my name for the process which joined the Paper-sums view through Conformal to the microviews of mental calculation, Miriam could see that the results of the processes SHOULD be the same and thus, the manipulations of the paper sums problems could make sense. The learning exhibited by the correlation of perspectives is different from that of the elevation of control in respect of the resulting structure. The Serial view intervenes directly in the functioning control structure of the mental calculation cluster. The Conformal view represents a species of knowledge essential in integrating disparate microviews — knowledge whose use is constructive but otherwise non-functional. Since the Conformal view does not enter into the control structure of the calculation microviews, we should not expect it to have functions within its own structure. The perspective of the Conformal view is a set of equivalences, e.g. a digit in this ten’s place is equivalent to a Decadal element [note 1]. This knowledge of other microview perspectives permits the coherent registration of one with another.
Perfection through Debugging
The crucial insight into the ten’s place value did not establish instantaneous coherence. First came the conclusion that the results of addition should be the same in Paper-sums and mental calculations, then came a working out of the value of the other places. For example, in her next two problems (77 + 23 and 137 + 256) Miriam used her mental calculation procedures to effect the carries required (arriving at the answer “tendy”, i.e. one hundred, for the first) but could not explain why this made sense in terms of place values. In subsequent sessions, we worked over a series of problems and applied a re-naming step to carrying. I criticized the rule “put down the N and carry the 1” as not making sense. We began renaming and marking the actual value of the carries, as Miriam had marked the actual place value of the “8” in the ten’s answer cell above. Thus Miriam’s “tendy” was renamed one hundred and the carry to the hundred’s column was as “100.” Similarly ten hundreds was renamed one thousand. Miriam declared that this system made sense, though her execution required the fixing of several procedural “bugs.” Thus, in the sum (a) below at left, Miriam treated the carry into the ten’s column as a ten and the 4 and 5 as units; she ignored the carry into the hundred’s column (in reaching 11) and probably disregarded place values entirely in the thousands.
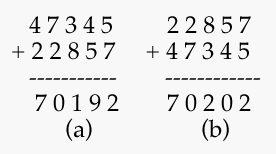
Miriam had shown me this result (a), believing it correct. When I pointed out her errors, she was so angry she refused to do any more calculations. Thus the second sum, (b) above, written on a clean chalkboard, was ignored for days, until Valentine’s Day, when Miriam executed the sum as a surprise present for me. Since that time, Miriam’s addition in this form has been essentially correct. Her confidence in her understanding was witnessed by the spontaneous extension of her addition skill to multi-addend multi-digit sums two months later.
Summary And Reflections
I have dwelt on one child’s learning to add as a worked example of a productive method for investigating and interpreting learning. The contribution of this analysis is the notion of separate microviews, derived from particular experiences, joining into a more powerful organization through structure-relating knowledge. Such relational knowledge is seen as different in application but not in kind from task-rooted knowledge. This analysis is a single, early step toward a computational theory of learning of general applicability, one wherein the specialization and refinement of perspectives expand and diversify the application of existing knowledges to new experiences while the counterbalancing processes of control elevation and perspective correlation permit the progressive integration of disparate microviews into a coherent mind. It is from the balance, the equilibration, of such countervailing processes of knowledge application-extension and integration that Piaget’s dialectical spiral of cognitive development appears. We can conclude that what is commonly called learning is the enhanced performance which emerges from changes within and between active micro views of knowledge.
A Summary of Miriam’s Addition Microworlds
We have seen four examples of significant cognitive development. The Decadal and Paper-sums views were related to tasks Miriam worked at, i.e. they are task-rooted microviews whose perspective elements describe things of our common world. The Serial view is a control view whose perspective elements are descriptions of subordinate microview perspectives; the sort of thing Serial “knows” is that Decadal can handle in general problems of the form “decade and units plus decade.” Similarly, elements of the Conformal view’s perspective are descriptions of elements in the perspectives of microviews it relates. These last two microviews coordinate the activity or perspectives of the microviews their perspectives describe. We have observed that the perspectives of the task-rooted microviews derive from the extensions and specialization of ancestral perspectives to make sense of experience in a new domain. Recall how the Money view descended from Count and how Decadal was a specialization of the Money view which was powerful in application because the Decadal denominations (decades and units) fit the culturally embedded representation of the hindu-arabic number system. We have argued for the competition of microviews in the formation of the coordinating views and noted the empirical result that the insights occurred when there was a surprising confluence of results where none was anticipated.

Why Knowledge from Disparate Experiences Can be Integrated into a Mind of Some Coherence
We should ask about those incidents of insight, because they derive from an unexpected confluence of microview outputs, to what extent the occurrence was either accidental or necessary. The particular incidents themselves have very much the flavor of accident, especially in the case of the Serial insight. Is it possible to argue that there was some sense in which Miriam was “fated” to make the discovery which integrated the Decadal and Count views for processing problems of a certain range of complexity ? We could argue, for instance, that the cultural embedding of the number representation would present any child with a multitude of problems over time which would promote her stumbling into a serial-like insight. Likelihood, however, is not necessity. Is there such a thing as a mathematical structure which was, in any sense, pulling Miriam’s cognitive development along a specific path ? It is not necessary to make such an assumption. What marked the stability of Miriam’s learning was the conjunction of ancestral microviews: the structure of the representation which we impute to Miriam is an emergent from her experience; its stability is based on the integrability of several experiences. That is, having multiple points of view is not magic; it was their fitting together that produced the stability. We have seen microviews of computation, each of whose perspectives analyzed problems into different elements for calculation. The significant aspect of number that results in developing complex and stable cognitive structures is not that there are “really” such things as “mathematical structures.”
Rather, the nature of number makes it amenable to calculations which go forward by anchoring thought at some element’s base-value and varying that base by some other term.
What the specific bases of number used in a particular calculation may be matters far less than that some base is necessary. It is this epistemological aspect of number’s structure (and its conformability to human thought processes) which permits a variety of views of experience to arise separately and subsequently to be integrated into a coherent and complex understanding.
Publication notes:
