LC0cA3 ^
Computer Microworlds and Reading: an analysis for their Systematic Application
Robert W. Lawler & Gretchen P. Lawler
abstract
Learning can be seen as a consequence of problem solving in particular cases. It occurs when one achieves a solution which is able to be used later. “Anchoring with variation” is a common and important process, providing a framework through which one can discuss coping with something imperfectly understood in terms of what is already well known. Our purpose in the following discussion is to explore some possible implications of this process for reading education as a worked example of how educational technology presents us with an opportunity for reconceptualizing instruction.
English has the phonological potential for more than 60 thousand monosyllables. Our analysis asks how many monosyllabic words exist in fact and what organization can be imposed on them to make the phonological code more accessible. We’ve chosen to represent these monosyllables as an initial phonemic cluster plus residue. The most common 550 residues cover 73 percent of the existing 7000 monosyllables. If children can learn 550 different correspondences between sounds and spelling patterns, their knowledge of these words, coupled with the ability to modify interpretations of letter strings by anchoring with variation, will cover a major portion of the phonetic-orthographic correspondences of the English language. We believe this extensive, concrete foundation of word and sound knowledge will permit children to read well enough that instruction will become primarily a refining and perfection of such knowledge.
The primary design conclusion is that if we create computer-based microworlds using words with the most common residues as the names for their entities and their actions, we will be providing a set of systematically generated monosyllabic anchors which promises to be highly effective for children’s interpretation of many words they will encounter in reading English. The potential revolutionary impact of such a pre-reading curriculum is worth exploring.
1.0 A PERFORMANCE
Learning can be seen as a consequence of problem solving in particular cases. Let us offer you one of our favorite examples of problem solving as a basis for discussing this issue.
A number of years ago, our son Rob, then age 8, and daughter, Miriam, age 6, were playing in the kitchen. They mixed together some flour, salt, and water to make clay, rolled the mixture out flat, and then folded it over time and again,. As they worked, Robby was counting the plies, the number of times he had folder the material. He counted 93, 94, 95, 96… By the time there were 96 folds, the materials was very unwieldy; so he took a large knife and cut the material in half. Placing the second half on top of the first, he said, “Now we’ve got 96 plus 96.” Miriam, who had not received any arithmetic instruction in kindergarten, responded, “that’s a hundred ninety two.” Robby was astounded, for he could do no such mental calculation although an able student in the second grade. Her performance was impressive for a kindergartner.
1.1 How She Did It
The reasons Miriam at six was able to compute such a result were two fold. First, she had come to recognize 90 as a number of special importance through using Logo Turtle Geometry with Bob at the MIT Artificial Intelligence Laboratory. Second, she had developed certain procedures for mental calculation with numbers of such magnitude. For example, she would be able to add 30 and 45 by saying that 30 and 40 is 70, plus 5 is 75. She had other knowledge as well. Of specific use in this incident, she knew from experience with turtle geometry that 90 degrees pus 90 degrees is 180 degrees. So, when Robby asked his mother if the result was correct, Miriam answered first and was able to prove her result — in the process revealing the particular knowledge on which her performance rested: “We know that 90 plus 90 is 180, and 6 is 186… [then counting on her fingers], 187, 188, 189, 190, 191, 192.” [1]
1.2 Anchoring with Variation
The formulation through which we would like to describe this mental calculation is one that we draw from the work of Tversky and Kahnemann [1974]. These investigators required of their subjects results for arithmetic and estimation tasks so difficult that the subjects could in no way calculate the results precisely; they then examined the difference between the estimates subjects made and the actual results of completed calculation. They use the phrase, “anchoring with variation” to label a specific kind of mental performance they observed in their experiments.
They found, uniformly across the subjects they studied, that the typical process of such calculations under conditions of the subject’s uncertainty was one where the subject anchored the problem solving process at a specific estimate and then varied that value to solve the current problem. So described, anchoring with variation has very much the character of analogy, in a specific, limited sense: the solution to a problem such as 96 plus 96 is analogous to the solution of 90 plus 90. But anchoring with variation functions like analogy until such time as the resulting solution becomes a salient entity itself, a well known thing or result. When this happens, analogy goes away. Anchoring with variation is an important process because it provides a general framework through which one can discuss the basic situation of learning, wherein one tries to deal with something imperfectly understood, by definition at the frontier of one’s capacity. Learning occurs when one achieves a solution which is able to be used later.
We will use their phrase, anchoring with variation, to label the kind of calculation that our daughter went through in this story. She began with one well known result: 90 plus 90 is 180. She anchored her problem solving on that result, and by two variations, the catenation of 6 and the finger counting of 6 more, solved the problem.
Does anchoring with variation occur in other domains? The following anecdote reveals the same process in another guise. Our second daughter, Peggy, at six years, was using a workbook which required that she draw a picture of a coat. She was stymied for a moment, then continued, “Coat… Oh. A coat is a person without any hands, or legs or feet, or a head, and with buttons.” She was anchoring a newly constructed idea of how to draw a coat on the representation of a person that she had developed in her drawing experience, and then varying the individual features of that already established model.
Such a process is common for many people in various domains of problem solving. The purpose of the following discussion is to explore some possible implications of this process for reading education as a worked example of how educational technology presents us an opportunity for reconceptualizing instruction.
2.0 CHARACTERISTICS OF THE PRE-READER
By definition, pre-readers have limited ability to construct oral words from letter strings. There are other, less definitive but still interesting, characteristics. Typically (but not uniformly) such pre-literates know that they are not readers. They make some very interesting meta-linguistic judgments. Children don’t know what words are before they know how to read in a very specific sense: they apply the term ‘word’ to what adults call ‘phrases.’ For example, if you ask how many words there are in the sentence, “A mother can carry her baby,” a pre-reader will indicate 4 or 5; “A mother can-carry her-baby” or “A mother can-carry her baby. [2]
2.1 An Example: How Reading Is Like Problem Solving
Even though they are pre-readers, children may still recognize certain written words, such as ‘stop,’ and identify them in other contexts. Other commonly well known words are ‘mom’ and ‘exit.’ Further, pre-readers are able to recognize some individual strings of letter symbols as words through a very strong use of context dependency. Consider this example from Peggy’s behavior near age six:
An anecdote: We were shopping for Christmas presents, shirts for our oldest daughter and son. We couldn’t find the correct sizes. “Well,” Peggy said, pointing to the bin labels, “over here they are small, medium, and large.” She couldn’t read those words as such. But she could recognize the initial letters of those words and she did know that the kinds of shirts we were looking at came in those three sizes. With this strong use of context, she was able to make a reasonable speculation as to what the three particular letter strings meant.
2.2 Expectations for Beginning Readers
In contrast with the pre-reader, a beginning reader should have considerable ability to recognize whole words. She should have an ability to decode words that are not recognized. She should have an ability to recognize words as significant exceptions to standard pronunciations.[3] An able beginning reader should be capable of decomposing polysyllables into monosyllables, decoding the syllable sounds, and assembling the parts to words whose meaning she can recognize. Of course, a reader should be able to understand the meaning of a sentence when she puts the words together.[4]
3.0 ANCHORING WITH VARIATION IN READING
3.1 The Particularity of Anchors
What are the anchors of calculation? If asked to calculate 96 plus 96, most people would justify their answer (192 if they’re right), “That’s two hundred minus eight.” The decimal number representation plays a key role in your ability to perform such mental calculations; simple multiples of ten are common anchors. There are other sorts of anchors of variation. For instance, if asked how much is 12 times 13, one might say “144 plus 12 is 156.” Such a response shows the person has memorized a series of results, the times tables, whose elements can serve as anchors of variation.
Children’s anchors for variation may be much more particular and specific than most people imagine, Before Miriam’s computer experience, she could not add 15 plus 15 because she “didn’t have enough fingers.” At the same time, she did know that 15 cents plus 15 cents was equal to 30 cents.[5] Similarly, adults with unusual experience may have surprising anchors of variation. People in the computer business think a lot about powers of two, and many can recite the binary power series: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 4096. Such numbers can become anchors of thought in terms of which other things are interpreted. A personal example can emphasize how particular experience affects anchors of variation: because he spent too many hours decoding machine language core dumps in hexadecimal, Bob can look at 96 plus 96 and see it as 60 plus 60, hexadecimal. That’s ‘C-zero’ (because 6 + 6 = ‘C’) which on reconversion into decimal is 160 plus 32. An individual’s anchors of calculation depend intimately on the particulars of his experience.
3.1.1. Anchors in Reading
Let us ask what could be comparable anchors of variation for the decoding of alphabetic words: one possibility would be those familiar words that just about all children know because they are encountered everywhere, things like ‘stop’ and ‘mom.’ Others might be family names: Bob’s name is well known to our daughter, as is the word ‘Scurry.’ Let us elaborate this last instance to emphasize the accidental character of these anchors. Our family pet is a Scotch Terrier, who as a little puppy used to scurry all over the place, and that’s what we called her. But that word is very well known to Peggy as a name. In general, these anchors are accidental and depend on experience as do those for mental calculation. Why is that important? Precisely because computer based microworlds introduce the possibility of creating materials through which a designed, non-accidental set of systematic anchors could be introduced to pre-readers.
If it were possible to create a more nearly complete collection of anchors for the interpretation of monosyllable words, we could change significantly the process of learning to read. We could make reading much more accessible to many more people in a relatively efficient and congenial fashion.
3.1.2 An Example of Anchoring in Learning to Read
In there any indication that a process such as anchoring with variation is relevant in learning to interpret words? Consider another anecdotal example. Recently, our daughter Peggy was sitting at the table in our kitchen reading a comic book; and she piped up, “How do you say ‘s \-o-b’?” and then continued, “It must be ‘sob’.” Bob happened to be there and asked, “Why is that, Peg?” “Well,” she said, “it’s ‘s’ with Bob.” The process of her interpretation is revealed by her justification: she began with “Bob” and /bob/, both of which and the association between which she knew well; she modified those entities to construct new entities whose similar association solver her reading interpretation problem. Anchoring with variation is a name for a specific form of problem solving by analogy.
As we turn to the systematic design of a set of reading anchors our attempt will focus on the learning of whole words, but it’s obvious you can’t learn only how to read whole words; you have to learn the phonological code. We conclude as follows: if this process of monosyllabic modification can become richly productive in the child’s everyday experience, and if the child has a sufficiently rich repertoire of well known words to modify, the invention of this procedure and its good development by every child should be expected; further, if such a result materializes, current phonics instruction will become largely obsolete. Seen from the perspective of anchoring with variation, phonics and whole word learning must and can be complementary. Mastery of the phonological code will derive through variations from recognizing a very well chosen vocabulary of whole word anchors.
4.0 A MICROWORLD EXAMPLE
Figure 1 shows the beach microworld Peggy played with, in some variations. Computer-based microworlds can be made which most children will find quite congenial.[6] The important functions of the world are the creation and manipulation of objects. An object is created through use of a word that is a named procedure; other words name procedures that manipulate that object.
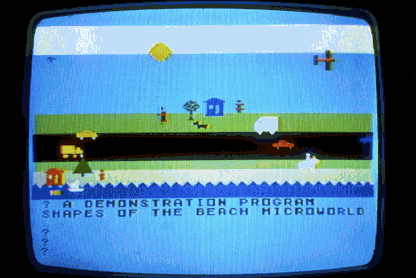
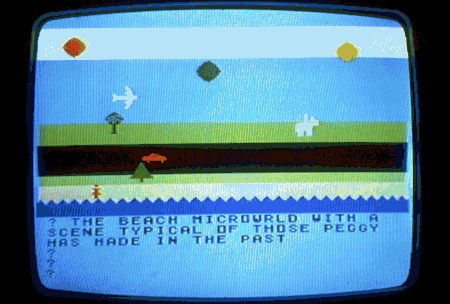


Using arbitrary symbol strings (which may be words) as the tools of her control, a child is able to make objects appear and to manipulate them in a virtual world that can be shaped to her own purposes. Even at the age of three to three and a half (when she first began playing with the BEACH microworld), Peggy learned with reasonable facility and permanence to recognize roughly thirty words. She recognized them by sight on the screen and in other contexts. She could re-create them from memory and did so, typing them on the computer keyboard. In this specific sense, she was the master both as reader and writer of that small vocabulary of words.
5.0 THE CENTRAL ARGUMENT
BEACH is only one microworld. There’s no reason why one can’t have a multitude of such microworlds, and there’s no reason that experience with a multitude of such microworlds cannot be based on a vocabulary which will present as anchors for variation the most productive words of the language.
5.1 Piaget and Curriculum Design
A profound theme in Piaget’s work is that the cognitive structures which support the development of mature skills may be quite different from what students of mind have previously supposed. Advancing the progressive development of these intermediate structures then is a central task of curriculum design. Computer experience will change these intermediate structures.[7] The rest of this paper is directed to selecting an English vocabulary to support the development of intermediate structures for reading skills.
5.2 Application to the Case
Using whole words and putting those words in contrast so that one might compare ‘up’ with ‘pup’ and ‘play’ with ‘day’ is something that has a long and respected tradition.[8] Our approach to the design process is, however, different.
Although final reading performances will appear similar, the path of development will move through different intermediate cognitive states. Let us suggest what those different states would be. We propose introducing the children to an increased number of whole words, distributed over a broad range of language sounds, by offering them experience with multiple, word-oriented microworlds at a very early age. Recognizing an increased number of whole words, 200 to 500, at the age of four or five should not be uncommon (Peggy at three recognized thirty words from the manipulation of one microworld).
Decomposing monosyllables into an initial phoneme and a syllabic residue is a pre-reading activity frequently introduced by language games played in small groups.[9] Breaking whole words into an initial phonetic cluster and a syllable residue would be worked out naturally using the vocabulary presented and established through experience with these multiple microworlds. Such would be the next, intermediate state of development. It would be followed by either the spontaneous or the directed reconstitution of other monosyllables through anchoring with variation.
The reading of monosyllabic text with help, then unaided, and finally reading polysyllabic text, would be the normal sequence of further states of development. The key difference is the early one of introducing a child to a multitude of monosyllables through computer based microworlds.
6.0 AN ANALYSIS OF ENGLISH MONOSYLLABLES
English is not a monosyllabic language, but we may be able to present it to pre-readers as if it were such. Why is that worthwhile doing? and how can it be done?
6.1 Learning to Read in Syllabic Languages is Easier
The standard report by adults of learning to read Cherokee, which has a syllabary of 85 signs, is that they learn to read in one day (Morris Halle, in Kavanaugh & Mattingly, 1972). This may be an exaggeration, but there’s a contrast of orders of magnitude in comparison to learning to read in an alphabetic language such as English.
A second example: in The Psychology of Literacy, Scribner and Cole discuss learning Vi, the traditional language of a people in sub-Sahara Africa. The written language is not taught formally in schools but is learned from friends when a person has a use for it. The sounds of Vi are represented by a syllabary of approximately 200 signs.
The sizes of these syllabaries (200 and 85 signs) indicate an order of magnitude of syllable signs people can easily recognize and distinguish as significant components of written language. If we ask children to recognize 200 words it’s probably not too much. As the following analysis shows, there are reasons for wanting them to recognize as many as 500 or more. That’s still probably not too many.
7.0 THE METHOD
The systematic approach we propose will cover the phonetic range of English in such a fashion that it will both make the structure of the language more comprehensible and make it accessible to the flexibility of computer implementation.
7.1 The Issue of Representation
We have to deal with how to represent the sounds of the language unambiguously and naturally. The atomic approach is that of the international phonetic alphabet (IPA): one symbol, one meaning.[10] Historically, alphabetic languages have represented single sounds with multiple characters, making it difficult to understand the correspondence between sounds and letters.[11] Choosing to deal with monosyllabic words focuses on the ‘molecular’ rather than on the ‘atomic’ level of symbol aggregation. This choice by itself offers children instruction in what are significant units in the written representation of language.
7.2 The Space of Monosyllables
If we’re going to represent the variable spellings of the english language and its sounds by a collection of monosyllables, we might wonder how many that would take. Consider the monosyllable as a vowel bounded by two consonantal clusters. There are 51 initial consonants and consonantal clusters in English. There are 14 vowels.[12] There are 87 terminal consonants and consonantal clusters.[13] English has the potential for more than 60 thousand monosyllables. Reducing the space of possibilities by excluding terminal clusters brings the number of potential monosyllables down to a more manageable size, defined by the 51 initial clusters, the 14 vowels, and the 21 terminal consonants. Call these approximately 15 thousand monosyllables (51 times 14 times 21) the reduced space; this is the material of our preliminary analysis. From preliminary analysis, the terminal clusters are excluded. Later analysis will proceed over the full space which includes terminal consonantal clusters.
7.3 How is That Space Populated?
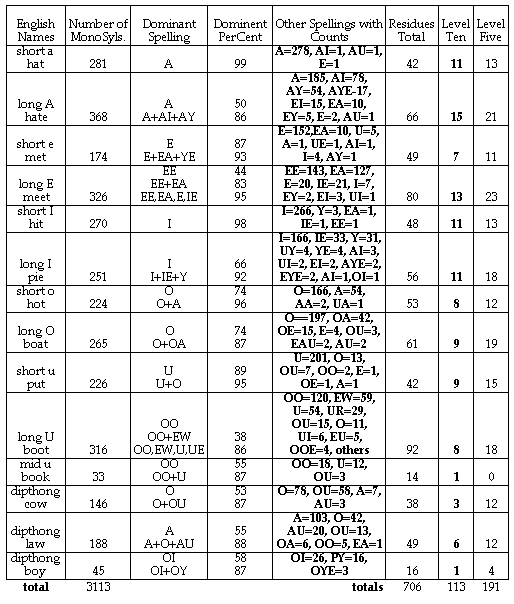
To determine the density of existing words in this space, we made a three dimensional matrix, in effect, and examined every cell. The primary result is that the space is about 20 percent full. Instead of the potential 15 thousand monosyllables, approximately 3000 actually exist in English. Figure 2 presents summary information on the members populating that space.
7.3.1 Organizing the Reduced Space of Monosyllables
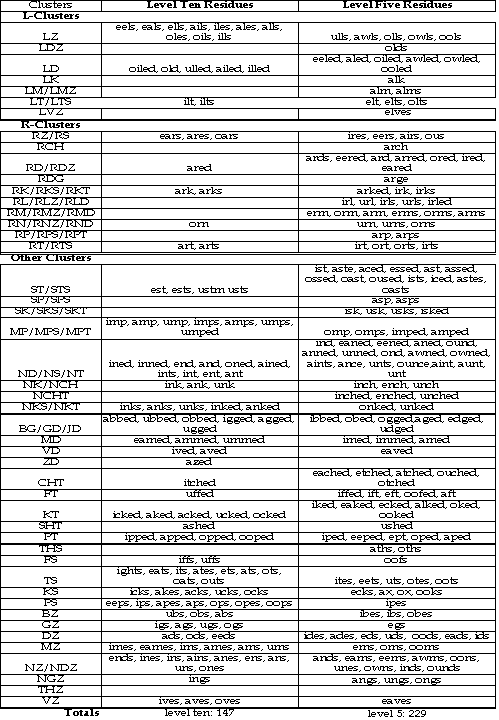
To bring this space of 3000 actually existing monosyllables under a systematic categorization, we’ve chosen to represent these monosyllables as an initial phonemic cluster plus residue, in the fashion that was exemplified by Peggy’s use. She made a residue of “Bob” and /bob/ by cutting off the initial letter and phoneme. How many such residues are there in the English language? Within the 3000 monosyllables of the reduced space, the number of residues is approximately 700. From these 700 residues, we can select those that actually appear most frequently in English monosyllables. Some residues appear in many words while others are rare. 113 appear in 10 or more monosyllables. Call this the set of level 10 residues. The size of this set is near the size of the cherokee syllabary. Similarly, there 191 (113 + 78) level 5 residues (those which appear in five or more English monosyllable words). This set has fewer members that the number of signs in the Vi syllabary. If children could recognize these two hundred residues, they would have a syllabic basis from which they could interpret 73 percent of the 3000 English monosyllables in the reduced space.[14] In this specific sense, these would be the optimally productive residues for pre-readers to recognize.

7.3.2 Extending the Analysis to Terminal Clusters
The major constraint applied in permitting generation of the reduced space of actual English monosyllables was restricting words examined to those with a single terminal consonant or none at all. But many words end with consonantal clusters. We have attempted to answer the question, “How many?” and to explore the organization possible to impose on them through a residue oriented analysis.
Generating the extended space of monosyllables with terminal clusters involved complexities absent from the generation of the reduced space. Almost any consonant joins easily with almost any vowel. Consonants, generally, do not aggregate so readily. The fact has a powerful influence on what words are possible in a language. We found out which consonants cluster together and generated the extended list of existing English monosyllables by following this procedure:
- We formed a square array with a row and column for each of the twenty terminal English consonants; the cell where a row and column intersects represents the terminal cluster formed by those two consonants.
- For each of these four hundred cells, we repeated the process through which we generated monosyllables for the reduced space. More specifically, for each terminal cluster we formed the two dimensional array intersecting the fourteen vowels with the fifty one initial consonants and clusters, pronouncing each triplet of initial cluster plus vowel plus terminal cluster, we tested for the existence of a word by our recognition of the sound.
- We supplemented this list with those few terminal clusters containing more than two consonants (e.g. twelfth)
The intention here was to generate a maximal list of possible words. Consequently, any sound which either of us considered a possible word was entered into the two dimensional array for the terminal cluster then, subsequently verified or rejected based on its presence in Webster’s Third New International Dictionary (1971 edition). Since the word list we generated is limited to those spelling sounds we knew or imagined to be words, ours is a personal list and it cannot be perfect. We can guarantee it is exhaustive. Even if others propose some few words we have not considered, we doubt that the conclusions of our analysis will be changed significantly.
This list, verified by dictionary entries, was then purged. We deleted words of these sorts: archaic words, arcane words, Scotch, English, and Australian dialectical forms; vulgar and insulting words. We found that of the 400 cells in the terminal cluster array, only sixty six represented terminal clusters from which English monosyllables are actually formed. These sixty six terminal clusters form 4280 monosyllables in addition to those of the reduced space, for a total of approximately 7000 monosyllables. Call this collection of words “Lawler’s complete list.”
7.3.3 Organizing the Extended Space of Residues
The character of the following analysis is determined by the ways in which consonants actually cluster together. In general, there are two quite different classes of clusters. The first is uncommitted as to meanings assigned to the consonantal cluster; it is dominated by words formed with the glides /L/ and /R/ as the initial member of the consonantal cluster. The second class is formed by the suffixation of the four inflectional consonants: /D/ and /T/, and /S/ and /Z/. /D/ and /T/ are used often to indicate temporal verb inflections, while /S/ and /Z/ frequently indicate pluralization of substantives or third personal singular inflections of a verb. There are nearly 1200 residues in the collection of the 4280 words in the extended space of monosyllables. Within this broad dispersion of sounds and spellings, there is nonetheless significant aggregation of words around residues, as shown by the summary table below:
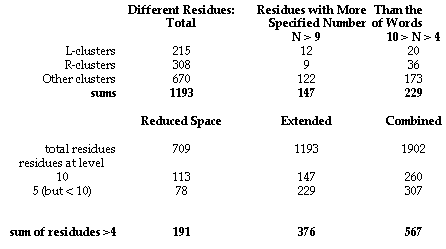
The summary of this analysis is that among the nearly 1900 different residue spellings of english monosyllables, those which appear in more than ten words number only 260. Those which appear in more than five words number about 550. The first number is clearly within the range of words knowable through the sort of associational memorization called upon within syllabic written languages. If children can learn as many as 500 or 600 different correspondences between sounds and spelling patterns, their knowledge of such residues, coupled with the ability to modify interpretations of letter strings by anchoring with variation, will cover a major portion of the phonetic-orthographic correspondences of the English language. We believe this extensive, concrete foundation of word and sound knowledge will permit children to read well enough that the instruction they will need will be primarily a refining and perfection of such knowledge. The 191 residues of the reduced space cover 2227 words. The 376 residues of the extended space cover 2974 words. Together, they cover 5201 words, a little more than 70 percent of the 7390 words in Lawler’s Complete List. The list of these 550-plus level 10 and level 5 residues is presented in Figures 3 and 4.
8.0 CONCLUSIONS
The primary design conclusion is that if we create computer-based microworlds which use words with these level 10 and level 5 residues as the names of their entities and actions, we will be providing a set of systematically generated monosyllable anchors which promise to be highly effective for childrens’ interpretation of many words they will encounter in reading English. The potential revolutionary impact of such a pre-reading curriculum in worth exploring.
A significant possible second outcome is that such experiences could alter the balance in the learner’s perception of the orderliness of language. One difficulty with English is that the most common words are often the exceptions to the rules of phonological correspondence. If we introduce children to microworlds through which they will have experience with words that are archetypical in terms of phonological correspondence, we may be able to change the child’s view of language from one where reading grows by the rote memorization of senseless letter strings to one of language as a rule-governed code with a lot of exceptions. More concretely, ‘dog’ is a very common word, but ‘jog’ is a common word too. If a child learns that ‘jog’ contains the characteristic spelling for the sound /og/, and that the residue also appears in log and bog and frog, then a child will be in a much better position to recognize explicitly that ‘dog’ is an exception to the orthographic-phonetic rules of correspondence. Such could be a very important development in respect of making the English orthographic code more comprehensible to children. If this approach works, we could make the orderliness more salient than the disorder; we could, in effect, change the salience of the figure and ground in the child’s early experience of the written language.
Notes:
In the course of this analysis, years ago, I had extensive aid in the generation and validation of English monosyllables from Gretchen P. Lawler, my former wife.
[1]. There is more to this story than the anecdote presented here. The persistent scholar will find more examples, more detail, and a discussion of the relation between her computer experiences and other knowledge in Lawler, 1985.
[2]. “Pre-readers’ Concept of the English Word” [Lawler, 1976] reports more details on such judgments and their variations, revealed through a checker-taking task derived from Karpova’s work, as described in “The Psychology of Reading,” (Gibson and Levin, 1975).
[3]. For example, the word ‘dog’ should be recognized as am exception to the standard pronunciation that’s usually represented by the letter ‘o,’ as in jog, clog, or bog.
[4]. There are other interesting characteristics. Bob’s research with kindergarten children showed that those who were in the threshold of being readers typically used exclusion arguments in justifying metalinguistic judgments. For example, in the sentence, “The puppy wants to eat,” beginning readers would assert that the /pi/ sound cold not represent a word because it was part of ‘puppy.’ Pre-readers, on the other hand, would agree that the sound /pi/ in ‘puppy’ was a word. They would say, “Yes. Of course. It’s the name of the round things you eat [pea].” Or, “Sure, it’s a letter of the alphabet.” Or “I don’t want to talk about that [pee].”
[5]. 15 cents was what she paid for her favorite chewing gum. She had 30 cents a week allowance, and she could get two packs of her favorite chewing gum for that amount of money.
[6]. The essential reason is that the flexibility of computer systems makes it possible to design objects and procedures within these microworlds which are tailored to the specific experience of a young child. The scene in Figure 1 represents a beach in our town where we played, collected shells, and so forth. This microworld contains many objects with which she is familiar, Such microworlds are adaptable for use in other languages and cultures. Miriam recoded BEACH for use with French words. It has been used by some of Bob’s colleagues from Senegal as a model of the development of microworlds for the children of their country. See Lawler, Niang, and Gning, 1983.
[7]. This claim is supported, in the large, by Lawler, 1985.
[8]. Dr. Seuss’s ‘Hop on Pop’ is the premier example of a reading book with such an objective. Curriculum designers have long produced materials based upon rhyming syllables. No one should be surprised to see computers as the medium for such materials today. The issue must be whether or not they embody some new idea.
[9]. One might begin with pig latin games for initial phoneme segmentation, as Harris Savin proposed (in Kavanaugh & Mattingly, 1972). There’s room for imaginative application of the technology to that particular problem.
[10]. A good description of English phonetics and phonology may be found in Lyons, 1968. In that text, the kind of analysis pursued here is called the syntagmatic combination of phonemes.
[11]. For example, in the IPA, Bob’s patronymic takes four symbols (LOLR). In English, 5 or 6 letters are common(LALOR, LAWLOR) while 12 were required for the same sound in the original Gaelic [LEATHLOBHAIR); English represents 44 phonemes with 26 letters whereas Irish encodes more than 60 phonemes with only 18 letters (Green, 1966). Accidents of history, as well as many to one coding, have complicated the English sound-letter correspondences (see “The History of English Sounds” in Robertson and Cassidy).
[12]. The middle sounds of these words are all the English vowels. FRONT: BY BEE BID BAY BED BAD BUT; BACK: BAH BOUGHT BOY BOAT BOOK BOOB BOUT.
[13]. There are 21 terminal consonants and basic clusters (/tsh/ and /dzh/) and 66 terminal clusters by actual count (about which more later).
[14]. The 113 level ten residues cover 1748 words and the other level five residues another 537. The sum 2285 is 73 percent of the total monosyllable count of the reduced space.
References:
Gibson, E. J. & Levin, H. (1975). The Psychology of Reading. Cambridge, MA. The MIT Press.
Green, D. (1966). The Irish Language. Cork: The Mercier Press.
Kahnemann, D. & Tversky, A. (1974). Judgment Under Uncertainty: heuristics and biases. Science, 185, 1124-1131.
Kahnemann, D. & Tversky, A. (1982). Judgment Under Uncertainty: heuristics and biases. London, New York: Cambridge University Press.
Kavanaugh, J. & Mattingly, I. (1972). Language by Ear and by Eye. Th Relationship between Speech and Reading. Cambridge, MA: The MIT Press.
Lawler, R (1984). Designing Computer Based Microworlds. In M. Yazdani (Ed.), New Horizons in Educational Computing. New York: John Wiley.
Lawler, R. (1985) Computer Experience and Cognitive Development. New York: John Wiley.
Lawler, R, Niang, M. & Gning, M. (1983). Computers and literacy in traditional languages. UNESCO Courier, March. London, H. M. Stationary Office. New York: Unipub, 345 Park Avenue, NY.
Lyons, J. (1968). Introduction to Theoretical Linguistics. London: Cambridge University Press.
Robertson, S. & Cassidy, F. G. (1954). The Development of Modern English. Englewood Cliffs, NJ: Prentice Hall.
Scribner, S. & Cole, M. (1981). The Psychology of Literacy. Cambridge, MA. Harvard University Press.
Publication notes:
Written in 1985.
Published in Instructional Science, vol. 14, No. 3-4, a special double issue dedicated to Artificial Intelligence and Education.
Republished in Artificial Intelligence and Education, Vol. 1, Lawler and Yazdani (Eds.), Ablex, 1987.
