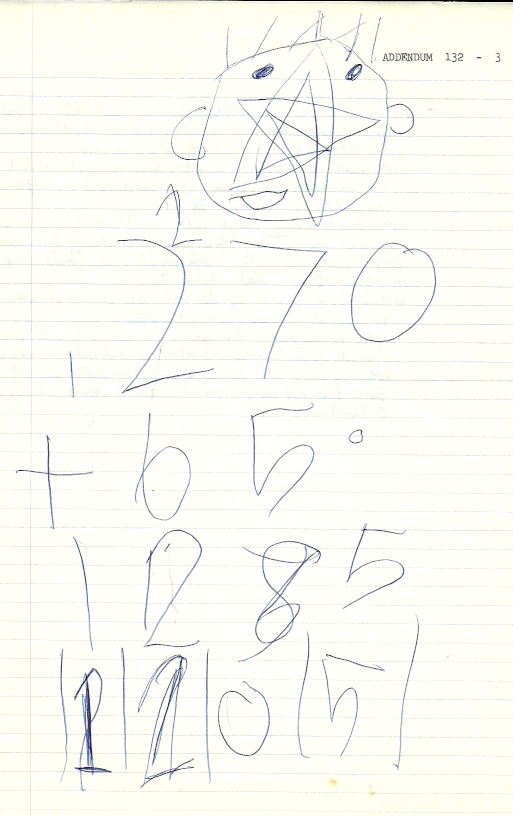Vn132.1 BIG-SUMS Extension 4/21 & 22/78
4/21 “Oog. I’ve got to add all these big numbers.” So I called to
Miriam’s attention a situation in which one could make use of the kinds
of skills she had developed in adding multi-digit addends: I was summing
the number of calories in my day’s diet. Miriam asked if she could add
the numbers for me. I protested that there were four big numbers to add
together and asked if she could do that. Taking a piece of note paper,
she replied, “I think I can do it.”
Miriam worked the problem of Addendum 132 – 1 in the notebook
I held on my lap. I expected her to perform 3 separate additions.
Instead, after I had read the first two addends (235 and 560) and Miriam
wrote them down in the vertical form, she asked me what was the next one,
and said she was going to do them all together. With the four addends in
place, she put in columnar division lines and plus signs, then underlined
each addend. I asked Miriam if she had been doing any such work in school
and why she underlined the addends. She answered “No” to the first
then question and “I don’t know. I just like to.” to the second. She declared
that this was the first time she ever tried “anything like this”, never in
school, and she had never seen Robby do it; she wanted to try just because
she thought she could do it.
The units sum was done first. As she summed the tens column
digits, Miriam asked for confirmation. “You put down the 4 and carry the
1, right?” I agreed. In the hundreds column, Miriam said, “You put down
the 7 and carry — no.” She wrote 17 in the hundreds column and continued,
“It’s 17 hundred and 45.” Then Miriam went on to draw her star and
added a ‘happy face’, which is her teacher’s symbol put on work well done.
4/22 As I recorded my supper calorie count, Miriam, who had a head
ache and felt too ill to eat supper, eagerly asked if she could add my
big numbers. (See Addendum 132 – 3). One addend I read as 12 hundred
85. As Miriam started to write 12 in the hundreds column, she asked if
it were correct. I told her another way to say the number was “1 thousand
2 hundred 85.”
She began adding at the left but immediately thereafter realized
there would be a carry-in and declared her first result an error. After
restarting on the right, at the sum of the tens column Miriam asked, “Do
you put down the zero and carry the 2?” I responded, “Do you think that’s
right?” She answered confidently, “Yes” and proceeded. When I inquired
whether her carry mark were a 1 or a 2 (it was initially illegible),
Miriam said “2” and rewrote it.
Upon her completing the sum, I asked what was the result.
Miriam answered, “2 thousand twenty five [for 2205]. Is that right?”
I said “No.” After a little while, Miriam said, “2 thousand 2 hundred
and 5.”
Later in the evening Miriam explained, “When I said that answer
had twenty five, I thought it was like the 2, 0 was twenty and then the
5, but I know that’s wrong.”
Relevance
I consider the incident of 4/21 an extraordinarily rich one.
Consider the precursors of the achievement. Miriam’s use of the standard
algorithm for addition in the cyclic notation is well-developed but
shaky, because of the difficulty of verifying the results of such a
computation. The second source is one Miriam denied (cf. Addendum 132 – 2)
as being like this problem. The triple single-digit sums of her school
work from last week clearly suggested to her the possibility of adding
more than two addends at a time. Her sense of the differentness of the
kinds of problems is evidence that she sees them as belonging to dif-
ferent worlds of thought and thus potentially connectible to different
cognitive structures.
The second significant aspect is that this problem shows as [an?]
internally directed extension of integrated knowledge as the elaboration
of a new procedure (handling triple single-digit sums) and its insertion
as a subprocedure in the controlling superprocedure Miriam uses for
multi-digit addition.
Finally, in drawing the teacher’s ‘smiley face’ on her own
math paper, Miriam shows herself playing both roles of ‘learner’ and
approving authority that is reminiscent of her playing both sides of
games at Tic Tac Toe.
In the problem of Addendum 132 – 3 Miriam confronted again
the double naming of ten-value hundreds as thousands and met her first
carry of value not 1. Her reading of the result suggested that with a
single, well-presented contrast of numbers to read, she should be able
to lock in the distinctions necessary to read any 4-digit results cor-
rectly. A day or so later, Miriam was able to read numbers from this
parallel list, and when shown the number names first, predict where the
zeroes and fives would appear.
5 FIVE 50 FIFTY 55 FIFTY FIVE 500 FIVE HUNDRED 505 FIVE HUNDRED FIVE 550 FIVE HUNDRED FIFTY 555 FIVE HUNDRED FIFTY FIVE 5000 FIVE THOUSAND 5005 FIVE THOUSAND FIVE 5050 FIVE THOUSAND FIFTY 5500 FIVE THOUSAND FIVE HUNDRED 5505 FIVE THOUSAND FIVE HUNDRED FIVE 5550 FIVE THOUSAND FIVE HUNDRED FIFTY 5555 FIVE THOUSAND FIVE HUNDRED FIFTY FIVEAddendum 132-1
Multiple Addends -1
Addendum 132-2
Schoolwork Sample
Addendum 132-3
Multiple Addends -2