The articulation of complementary roles
Given that the mind is a personal and essentially private construct, understanding learning requires a vision, at least, of how particular experiences from an individual’s social life relate to that personal construction of mind. The requirement can not be avoided when the experiences involve the interaction of one person with another — as in competitive games. What I offer here is a description, not a theory. This is not a mere description, however, but one with aspirations. One contribution by Winston (1975) was his observation that a particular description, through processes of part and relation emphasis, could come to function as a “concept.” One could say such a description aspired to be a concept of that class of objects. [I call such an aspiring description an ur-concept, after the German.] What I struggle to develop is an ur-theory of how social experiences generate the personal construction of the individual mind. I begin through the following example and use it as a guide for interpretation through the body of the chapter.
PRELUDE
Miriam has a long history of joke telling and invention. The following vignette is about her sister Peggy, two years old at the time. Their relation is basically amicable but also more than that.
Peggy imitates us and her siblings and has begun imitating Miriam’s knock-knock jokes. This was Peggy’s first form of joke imitation:
| Peggy: | Knock-knock. |
| Bob: | Who’s there? |
| Peggy: | (Broad laughter). |
That first night, Peggy plied her joke upon me time and again. It was amusing enough because of her imperfect command. We both enjoyed it. Eventually, the joke became wearing. I tried to begin the joke with her. When I began “Knock-knock,” she did not reply; I would say she could not reply. I tried many times. Even though she sensed something was expected of her, she did not reply.
The next morning I heard Peggy talking to herself in her crib: “Knock-knock. Who’s there? [Laughter].” Later, when she was brought down to breakfast, I cooked Peggy a muddled egg and we sat down to eat. Her first words were “Knock-knock,” and I responded appropriately. In my turn, I tried again:
| Bob: | Knock-knock. |
| Peggy: | Who’s there? [Laughter]. |
That same afternoon, Miriam confirmed my observation, “Dad, Peggy can say ‘Who’s there’.” I consider this a very simple and lucid example of the processes of the articulation of complementary roles.
Here is how I describe the elements of the example. Someone, a learner with (most probably) a relatively inferior comprehension, is engaged socially with more comprehending people — in this case focused around what is literally a script for a joke’s telling. The reasons for their common engagement may be of any sort, friendly, helpful, even antagonistic. During the engagement, the social demands push at the boundaries of comprehension of the person with the undeveloped perspective. Peggy was regularly asked “who’s there?” at first, but later she was expected to respond that way herself and could not. Subsequently, in a period when deprived of that social engagement, the learner recalls and recreates that kind of engagement, compensating for the solitude by simulating the role of the other actor. The first type of process I call homely binding (“homely” being a contracted form of “home-like”): the learner attaches herself to uncomprehended “routines” of engagement (in both the theatrical and programming senses). The process may be friendly or not so — but it is more aptly and generally described by that wide ranging class of intimate relationships that characterizes the interactions of a small society, the home.The second type of process, lonely discovery, occurs when the learner is deprived of social engagement — left to her own devices — and uses those devices to re-enact the uncomprehended experiences. This simulation of the other actors imposes a real demand for the distinction between roles and their relations which was lacking in the initial engagement. My name for this pervasive and oft repeated sequence of homely binding and lonely discovery is the articulation of complementary roles.
The relation of social experience to personal construction is that more integrated discriminations are required for controlling multi-role enactment of scripts than are required for acting in them. On the stage, an actor may memorize his lines and take cueing from the tag end of a fellow actor’s preceding speech. An actor, or a learner, in taking on two roles must do more, must not only cast herself in the second role but must also function as director of the entire scenario. The director’s function (a global control of the script’s progression as distinct from serial cueing) requires the articulation of roles; executing this function requires reflection and leads to a refined comprehension of the script.
Our example of Peggy’s learning knock-knock jokes does not, of itself, distinguish between a better articulation of a serial process and the creation of a control element which functionally has subordinated pre-existing structures. We do so now. Peggy never began “Farewells” herself, but when someone else initiated an interchange by saying “Goodbye, Peggy,” she would reply “See you later.” In such a separation protocol, she played rigidly the respondent’s role. Two days after her better articulation of the knock-knock joke script, Peggy used this rigid protocol as the content of directed speech, thus:
We were in the same room, had played for a while, and she decided to leave. At the door, she turned to me and said, “Say `Goodbye Peggy’.” “Goodbye, Peggy,” I repeated. “See you later,” she responded as she left the room.
From these incidents I take the following conclusions. The relations Peggy worked out for controlling what is said when playing an alternate role in the joke affected her ability or inclination for the more explicit control of speech. This is true even for other exchanges which might not seem to us so strictly conventional as the more recognizably stereotyped joke script. [One can not argue coercively that this single incident must have been the sole generator of such a change. On the other hand, if particular experiences are the foundation for cognitive development, then some one among them must have been the first. This experience clearly exhibits a set of characteristics which seem essential to the process.]
These incidents provide a succinct example of how the articulation of complementary roles creates new control structures in the mind. I now offer in detail a much more elaborate case study of the articulation of complementary roles, one spanning several years and interleaving the functioning of highly specific knowledge developed through homely binding and the creation of refined control through lonely discovery. This study builds slowly, appropriately so, because that reflects the character of the cognitive processes traced. Impatient readers may want initially to skim the section ‘Homely binding’ to read the more novel discussions of ‘Lonely discovery’. A critical reader will need to read closely the section on ‘Homely binding’ to follow the later interpretations.
INTRODUCTION
Tic-tac-toe is generally considered a trivial game and lacks an extensive literature, but I believe its study permits the raising of questions similar to those which have drawn the Artificial Intelligence community to the study of chess: what is the nature of expert knowledge? how does a novice become an expert? If the game is so simple as to be child’s play, its study in significant extension can be the foundation for worthwhile appreciations of how learning happens. In comparison with the lifetime of learning chess requires, this simpler game has the right balance for observing the development of knowledge.
The markers typically used in play, “noughts and crosses,” exhibit the state but not the progress of a game and are thus not adequate for our analyses. To indicate the sequence of both players’ moves, I represent Miriam’s markers by letters and those of her opponent by digits. The first marker of the initiating player is duplicated at the top of the grid. Game (a) below is recoded in this system as game (b).
noughts sequenced cell
and crosses recoding numbers
A
X | X | X C | D | B 1 | 2 | 3
----------- ---------- ---------
O | X | 2 | A | 4 | 5 | 6
----------- ---------- ---------
O | | O 1 | | 3 7 | 8 | 9
(a) (b) (c)
I will refer to specific cells of the game grid by the numbers given in (c) above. Individual games from the corpus will be referenced numerically by session and serial number; e.g. “2.3” is game number 3 from the second session played. Where appropriate, the session’s date will be specified with age-relative dating; for example, “6;1;5” means the games were played when Miriam was six years, one month and five days old. All Miriam’s publicly manifest behavior relevant to tic-tac-toe is captured in the corpus and a significant selection of that behavior is presented here. For the purpose of analysis, I developed the classification of games presented in Figure 4.1. The game labels, such as M1 and C3, will be used to characterize individual games in the text.
TIC TAC TOE: Twelve Opening Games
MIDDLE OPENINGS
---------------
A A
| - | B 2 | | C
----------- -----------
- | A | - | A | *
----------- -----------
1 | - | * | 1 | B
M 1 M 2
TRAPS WIN
CORNER OPENINGS
---------------
A A A A A
A | * | C A | | * A | | 1 A | 1 | * A | | -
----------- ----------- ----------- ----------- -----------
2 | * | 2 | C | 1 2 | * | 2 | C | | 1 |
----------- ----------- ----------- ----------- -----------
B | | 1 B | | * B | | C B | | * - | | B
C 1 C 2 C 3 C 4 C 5
WIN WIN WIN WIN TRAPS
SIDE OPENINGS
A A A A A
1 | | * | 1 | * B | | 1 | | - | - |
----------- ----------- ----------- ----------- -----------
A | | A | B | 2 A | C | * A | 1 | - A | - | 1
----------- ----------- ----------- ----------- -----------
- | B | - C | | 2 | | * | | B | B |
S 1 S 2 S 3 S 4 S 5
TRAPS WIN WIN TRAPS TRAPS
NOTES:
"-" means the opponent can be forked if he moves here
"*" means this a cell where the initiator may win after his
opponent's next turn; two such imply a fork.
Different expert wins from those shown are possible. For example,
in game C3, move B in cell 9 is a winning move.
The critical move is each game, the CRUX I call it, is the second
move of the opening player. In expert play, this move is used both
as an element of the fork and to force the opponent's second move
to an innocuous cell.
Tic-tac-toe versus addition
This study continues the program of “The Progressive Construction of Mind” (Chapter 2 of Computer Experience and Cognitive Development), exploring a vision of learning as changes in the organization of separate and distinct cognitive structures through detailed analysis of case study material. While that chapter described Miriam’s learning of addition, this describes her learning about tic-tac-toe during the same period of time. The primary contrasts derive from the nature of the material, in three specific senses. Addition is a problem solving process that can go forward in a single mind, whereas tic-tac-toe involves essentially a second person (or a second person’s role, at a minimum). Further, learning addition involves an extensive knowledge of number which children typically construct in different settings over many years’ time. In contrast, tic-tac-toe apparently lacks so long and broad a dimension in personal cognitive history. Finally, criteria for what significant learning might be in respect of tic-tac-toe are not so obvious as they are for addition. The interpretation also differs from that of Chapter 2. In the context of a cyclic series of problem moves (as opposed to problems solved in a single pass), it focusses on the development of interactions between microviews at a slightly “higher” level of control. The central technical formulation is that a structure which begins as a socially governed convention for a series of interactions provides nodes at which later, internally generated decisions can affect behavior. The empirical material provides examples of what this means.
Agreeing that around age six children first become capable of putting themselves in others’ roles, scientists of various paradigms have raised the issue of how another becomes a part of the self; each has provided a characteristic vision. Freud, for example, proposed that the other within the self derives from the introjection of parents. I offer an information processing perspective, in the broad sense, on that question: the ability to imagine the thought of another develops from the splitting apart and subordinating of alternative structures within the self; further, whatever the cause may be for such development, we can trace its occurrence in experiences with problem domains whose particular structure permits essentially different sorts of problem solving activities to proceed. [A reasonable objection may be raised here: having an agent in the mind, such as the super-ego, is not the same thing as being able to imagine oneself in the role of another with that agent’s character. Exactly so. How the latter ability derives stepwise from the former is a central theme of this detailed analysis. See especially the sections “Table Turning,” “Two in a Row,” and “Playing Against Herself.”]
DESCRIBING THE INITIAL STATE
Tactical Play
The first two sessions of games permit characterization of Miriam’s play before any didactic interventions.
Two Games Representing Others As Well
(age 6 years; 1 month; 5 days)
A A C | | 2 B | 3 | E --------- --------- 1.1 D | A | 1.2 4 | A | D --------- --------- B | 1 | 3 1 | C | 2 M 2 M 1
(M1 and M2 are respectively the designations of the middle-and-corner and middle-and-side opening games from the classification of Figure 4.1.) Whenever Miriam initiated a game with a middle opening and I responded with a side cell, as in game 1.1, she won.She did not refer to these games as involving any sort of “tricks” (her word for strategy). When I altered my responses to a corner cell, we came inevitably to a draw, neither of us making any mistakes. The games above show Miriam winning a game (1.1), blocking a threat (move “C” of 1.2), and selecting unforced moves by preference. (I do not believe Miriam planned the fork she achieved in game 1.1 but can not prove she did not.) Her performance — based on knowing the rules of play and preferences for center and corner cells — was roughly equivalent to that which would be generated from activation of the production system (abbreviated as PS) offered by Newell and Simon (1972, p.62) as embodying what “is generally regarded as a good strategy for the first player.”
Simple tic-tac-toe production system model
side-to-move = opponent -> stop
center = blank -> play (center)
This computer-initiator always opens in the center, sets the M1 traps, and achieves the M2 fork. [This simple rule system can be modified for the second player by adding an eighth rule of the following sense: when the opponent has occupied opposite corners, move in any blank corner. Such a program seems to represent well the computer program against which Miriam played, as described in the upcoming section “Corner Openings”.]
How rough was the fit between the Newell-Simon PS and Miriam’s play can be clarified by the following four dimensions of contrast. First, although the moves generated by the PS and Miriam were similar, the thought behind them was quite different. Newell and Simon as mature players observe that “since the game is draw when viewed from a game-theoretic standpoint, good means here a strategy that will guarantee a draw and that will give the opponent as many opportunities as possible of making a losing mistake. Miriam did not play with the stability of well reasoned knowledge nor with the commitment to winning common in older players. To her, it was more important to be engaged in the game than to win it, and it was more important that the engagement be fair in her judgment than to continue playing. Next, even if her dominant play was well represented by the PS, two extrinsic sources of influence on underlying structures, boredom and social suggestion, modified her performance. (Playing the “same” game too often led to variation. Even given that her dominant microviews would propose a corner move before a side cell move, a social challenge, such as “Why do you always move in a corner?”, could lead to the rejection of corner move proposals with the resulting side move manifest in behavior.) Further, how she played depended on whom she played. Finally, the PS does not distinguish between strategic and tactical play, which came to be a major functional distinction in Miriam’s play. So that we may better understand how Miriam’s later play developed from this irregular beginning, let us enrich the characterization of her initial state, first by presenting a little background and then by recounting a specific incident which directed her thinking about tic-tac-toe in all subsequent play.
Two years before our study began, I bought Miriam’s brother Robby a tic-tac-toe game, which I introduced to both children. Miriam, then aged four, learned that one took turns and that winning was getting three counters in a row. I advised the children to look for “two ways to win.” Robby (then six) was able to absorb the instruction easily enough, but Miriam could not. At most, she learned that there could be such a thing as a fork (any move which creates two ways to win) but did not learn how to create one. They played with different competences: Robby winning with an occasional fork; Miriam winning frequently enough when he made errors to be satisfied. As Robby came to make fewer errors, they played less and the game dropped from their repertoire of favorites.
Corner openings
Combining the objective of achieving a fork with a specific plan for doing so entered Miriam’s game playing through the following adventure. Shortly before the beginning of The Intimate Study, I visited the Boston Children’s Museum with Miriam, Robby, and his friend John. One single incident made a tremendous impression on Miriam and markedly influenced all her subsequent play. John and Miriam both played tic-tac-toe against the Museum’s computer with openings M1 and M2. When they fell in the pitfall of a side response to the computer’s invariable middle opening, they were regularly defeated. The computer — which could be accurately described as playing with the Newell and Simon strategy, supplemented by the defensive extension noted earlier — always responded in the corner to their middle openings, so the children’s best game was no better than a draw. Eventually Robby got a turn (the others peering over his shoulder) and opened with a corner move. The game unfolded as below, and Robby won.
Three-corner fork
A
A | D | C letters: Robby
----------
| 1 | 3 numbers: computer
----------
2 | | B
C 5
John and Miriam were astounded. Robby clearly owned some powerful knowledge. Since he was glad to share that knowledge with them, the three-corner fork entered Miriam’s repertoire and exerted a dominant influence in the development of her play. Tic-tac-toe became a game of frequent choice as The Intimate Study began. This incident shows a socially current but uncomprehended slogan (“look for two ways to win”) given a personal meaning by the close observation and imitation of another’s striking performance. This particular form of the game is my archetypical example of strategic play. It is quintessentially a game length plan for the single player — as contrasted with the single moves, either choices or responses, of tactical play.
The limits of what Miriam learned from imitating Robby are shown by the remaining games of session one, wherein Miriam introduced corner openings. Game 1.3 duplicated the play by which Robby had defeated the Museum’s computer. What became increasingly surprising as I probed her play was Miriam’s rigidity in this form.
6;1;5
A A A A | 3 | C A | | A | 2 | C ----------- ----------- ----------- 1.3 | 1 | D 1.4 | | 1.5 | 3 | ----------- ----------- ----------- 2 | | B | | 1 | 1 | B C 5 C 1 C 2
When she confronted an opposite corner response to a corner opening in game 1.4, Miriam did not know how to proceed at all. Her response was primarily social: she complained loud and long. Eventually she moved with no coherent objective. Her inability to counter an opposite corner response in game 1.4 shows the rigidity of her strategy. Game 1.5 shows Miriam continuing with a three-corner fork objective despite move “2” rendering the as-yet-unachieved-fork completely ineffective. Apparently, she did not consider the relation of my moves to hers at all. Further, her not recognizing her own winning move (“C” in the middle, cell 5) establishes how disparate are the microviews of this strategic play and the microviews of her pre-strategic play. If we conceive of the strategy as a specific, three-move plan, the strategic microview can be seen as quite different from other microviews which recognize and seize opportunities based only on the current state of the game.
Turns at winning
In games 1.4 and 1.5 (played against me), Miriam met two impediments to her three corner objectives. In the games of session two against Robby, she did not adopt either of those specific moves as defenses. In surprising contrast, she attempted victory by negotiation. Game 2.1 below shows Miriam falling into the trap (move B) of opening form C5. Either she could not defend against that opening or did not choose to do so. I believe she initially accepted that loss, hoping to be allowed to win in her turn. But Miriam had come to doubt that Robby would play “fair” by her standards; thus in game 2.2 she tried to avoid going first (in her turn) because she believed Robby would block her attempt to occupy three corners: “I’m afraid he will take the place I want to go. I won’t get two ways to win.” Whom she played controlled whether or not she played with a game length strategy.
6;1;14
1 A 1 A
2 | C | 3 1 | C | 2 2 | | B A1| | 1b
----------- ---------- ----------- -----------
2.1 | A | 4 2.2 | A | 4 2.3 | 3 | 2.4 | |
---------- ---------- ----------- -----------
B | | 1 D | 3 | B A | | 1 A2| | 1a
C 5 M 1 C 3 C 1
The extreme of this opponent-specific tension — in relation to her expectation that she should be allowed to win games in her turn — surfaced in the play of game 2.4. Miriam’s fear that her corner opening strategy would be blocked resulted in her attempt to negotiate a victory:
| Miriam: | Are you going to block me? |
| Robby: | No. |
| Miriam: | [Puts marker in upper left corner – A1]. |
| Robby: | [Puts marker in lower right corner – 1a]. |
| Miriam: | [Shifts her marker to lower left corner – A2]. |
| Robby: | You took your hand off it! [outraged gripe] |
Miriam’s concern was that Robby not block her diagonal way to win (by occupying cell 9). Her switching to the adjacent corner was an attempt to avoid his blocking of her second step. When her functional resources were exhausted, she negotiated and cheated. (Of course, he lied.) The explosive disagreement which concluded game 2.4 ended their play for the day and up through session 14 (five months). Beyond noting the influence of the opponent on the choice between strategic and tactical play, we may conclude that Miriam judged winning as subject to a turn taking convention whose failure to be respected justified abandoning play altogether. (This was not unreasonable of her, for the game is played in alternating moves and alternating the first move is common.)
An initial sketch
On the basis of this characterization of her initial play and thought, let us ascribe microviews to Miriam covering the main points of the verbal description. Figure 4.2 is a sketch of the tic-tac-toe microviews I ascribe to Miriam at the beginning of The Intimate Study. Because we can clearly identify the incident through which strategic play first entered Miriam’s tic-tac-toe repertoire, we can confidently assert that her play was of two major kinds, strategic and what I call “tactical,” implying by this latter term a shorter planning scope. More simply put, strategic play has a game length objective; tactical play only focuses on one move at a time.
Once she learned about the three-corner fork — the knowledge effecting which is the content of the Corners microview — Miriam’s failure to block the threat of game 1.5 argues that when the Corners view was active in a specific game, tactical play did not operate. That is, strategic and tactical are alternate modes of play. Miriam regularly preferred strategic to tactical play. Nonetheless after the beginning of strategic play, Miriam’s tactical play remained operative, functioning in a default capacity when she did not move first (and thus could not get enough corners for her fork) or when she consciously avoided the only strategy she knew.
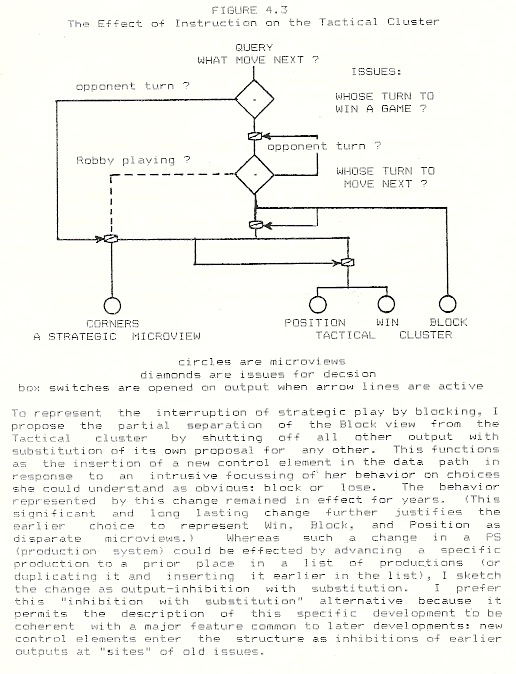
Even a rough sketch should respect the need for a system of such structures to function in playing the game. They should be able to propose a reasonable move at any time and to inhibit moves at the “wrong” time, i.e. one should not move out of turn but should respect the basic rules of play. The flow of information follows an “input/output” cycle; because we assume microviews are fundamentally active, we describe this as an acquisition/proposition cycle. Somehow is presented query, a question, “What move next?”, and information (the markers already in place in the external grid). Upon acquisition of input, the microviews propose moves. Miriam did not attempt to make every move she thought of, only those possible in her turn. The game issues represent such contextual control as the rules of the game require. For example, within each game, one must not play in the opponent’s turn. Further, one must decide who should move first in a given game. Miriam’s play showed numerous times that she was inclined to move out-of-turn, knew what specific move she would make if it were her turn. She inhibited her action, not her thought. I show the impact of these issues on play as inhibitions of microview output. One major issue is “how to play this turn?” A second set of issues, quasi-contractual, addresses the question of whether or not one should be playing tic-tac-toe at all. For Miriam at the age of six, her criterion of a fair game contract was that she be allowed to win in her turn, which we indicate with the question, “whose turn to win a game?” The issues’ potential for inhibiting output is indicated by a normally-closed switch on the output data path. [Information always flows in. They open only during the output phase of the move cycle. Behavior is selectively inhibited. Similarly, the preference for strategic over tactical play is shown by the output of the Corners view inhibiting the output of the tactical cluster.]
HOMELY BINDING
Forced Moves
In the preceding section, I chose to describe Miriam’s tactical play as a cluster of three competing microviews. One of the reasons for that choice derives from the specific changes in her behavior after I taught her to make forced moves. The sessions represented by game sets three through nine were didactic but in no way formal. Typically, Miriam sat in my lap and asked to play tic-tac-toe after we finished “doing some adding.” My instruction was at first no more than a response to and a reflection upon some immediately preceding action of Miriam’s, to help her understand and fix missteps of her play. Early on, I introduced a “loud thinking” style of play focused on making forced moves and explicitly considering what the opponent would do in turn. When Miriam failed to establish an attempted three corner fork in game 3.1 (not shown) because she pursued that objective instead of blocking a threat, I emphasized verbally the role of forced moves in play, thus in game 3.3:
| Bob: | Now you have one way to win there (A-/-B). I am forced to move here (moves 2 in middle). |
| Miriam: | I am [i.e. forced to move; moves C, blocking 1-2-/]. |
| Bob: | Yes. You are forced to move there. Now you have one way to win there (B-C-/). I am forced to move here [moves 3, blocking B-C threat]. |
| Miriam: | [tooting noises]. |
| Bob: | Do I have one way to win ? Yes. You are forced to move down there. |
| Miriam: | [Moves D, thereby blocking 3-2-/]. |
| Bob | You have one way to win there (B-D-/). I am forced to move there [moves4, blocking B-D]. |
| Miriam: | X ! [moves E, blocking 4-2-/]. |
| Bob: | So that’s a tie. |
6;1;16
A A A B | C | 3 A | C | 3 B | 1 | ---------- ---------- ----------- 3.3 4 | 2 | E 3.5 4 | 1 | 3.8 C | A | D2 ---------- ---------- ----------- D | 1 | A D | 2 | B 3 | D1| 2 C 4 C 5 M 2
With this external verbal support, Miriam for the first time subordinated her three corner fork plan to blocking a threat. In game 3.5, she made forced moves C and D without specific direction to do so. That is, as we played in this cooperative mode of talking about our reasonings, Miriam was able to subordinate her Corners objective to the threat-blocking requirement of standard play. Miriam’s learning to block threats is an example of homely binding.
Her success at taking advice on blocking makes even more interesting Miriam’s inability to take the next step. In game 3.8, she preferred blocking the threat (3-/-2) with D1 to winning with move D2. (The occurrence of her fork is not the result of a strategic plan. I consider it most unlikely that she intended to achieve this fork yet failed to recognize it.) Because she preferred blocking to winning directly in this game, I codified for Miriam a list of ordered rules for playing tic-tac-toe:
| Bob: | The number one thing you look for [writing a list], you say “Can I win?” |
| Miriam: | Can we stop for a while? |
| Bob: | Yeah. The second thing is: forced moves. And the third thing is what?… Two ways to win. |
| Bob: | You move first. You’re starting with an X. I’m going to go right where you went. Let’s see if you can beat me just the same way I beat you. |
| Miriam: | Wish. |
| Bob: | Is that the same way? |
| Miriam: | Did you go here? [cell 3] |
| Bob: | Yes. So you’re going in the corner now. [Miriam moves B] Now, this [2] is a forced move, because you have one way to win, so I have to go here. |
| Miriam: | [Placing C] Two ways to win ! |
| Bob: | Yes, you do. And you went over here [C of prior game] so I will too [move 3], and you beat me [as M. moves D]. |
| Miriam: | [Cheering herself] Yaaaaah ! I won for the first time. Hooray ! |
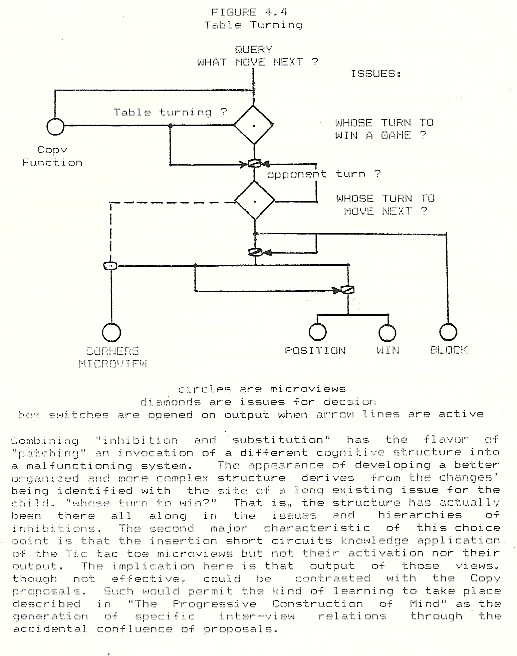
From Miriam’s penultimate comment (“Two ways to win”) it is clear she recognized the fork when she achieved it through table turning. I tend to doubt she had the fork in mind as one capable of being a strategic objective. (By contrast, the three corner fork was surely a strategic objective).
Results of early instruction
What, precisely, did Miriam learn from table turning? The games and dialogue of this period witness her effective play — and also the limitations of her understanding. Table turning helped to fix, at least temporarily, specific game results in Miriam’s mind. That is, Miriam believed she could win games with openings C1, C2, C3, C5 and often did so. Her learning to apply specific expert playing patterns through table turning is a second example of homely binding. I think of Miriam’s judgment that specific openings lead to victories as associated properties of multi-move patterns raised to salience by the very emphasis of my asking questions about them. Further, as witnessed by her not distinguishing between games permitting common forks, it is clear that what was most important to her in the definition of a game was her own pattern of action; for Miriam, tic-tac-toe at this time was an active game but not yet an interactive game. [Her one-sided play is thus reminiscent of the egocentric speech Piaget documented in his early study, The Language and Thought of the Child, 1926.]
Finally, Miriam’s ability to predict victories with games of specific opening patterns raises the issue of how her playing knowledge was related to knowledge about the outcomes of play. This is an important question; the later section “A stage change” will be dedicated to it. A preview of our conclusion there is that at this point in time (around age six and a half), Miriam’s predictions of victory were known as associated properties of opening patterns and not as game-length deductions from playing knowledge.
The idea of table turning — as contrasted with ordered rules — was easy for Miriam to assimilate for at least two reasons. First, table turning was a socially approved method for alternate winning which could displace the unacceptable method of public negotiation. (Two years later, when Miriam could no longer remember how to turn the tables, she still remembered that it was a method for her to win in her turn.) Second, the procedure was based on copying. Our markers were usually written in different colors of ink and the sequence of markers was always preserved (we typically used either letters or numbers as markers). Copying is a very primitive activity, and one unrelated to prior game knowledge. The moves of table turning were substituted for the normal outputs of Miriam’s microviews. I indicate Copying in Figure 3 as both switching off the output of the Tic tac toe microviews and proposing its own moves. In effect, I describe it as the insertion of a choice point for the invocation of another disparate microview, attached to the issue “whose turn to win a game?”
OPENING ADVANTAGE
Miriam propelled herself to independence, as the analysis of this section shows in detail. She had been my captive antagonist at tic-tac-toe for some five months when, while I was distracted otherwise, she engaged Glenn, a Logo project colleague, in play. I decided thereafter to terminate instruction as such and attempted merely to evaluate what Miriam had been able to learn. (My intentions as her opponent in sessions 11 through 16 was not purposefully didactic — though it’s hard to keep the doctor down.) Miriam at six and a half held her own with a brother two years her senior and with our games-knowledgeable colleague Glenn (some mere twenty years her senior). The most surprising observation of this period is that Miriam did not appreciate opening advantage at all.
On her own
At the end of session 7, Miriam refused to initiate a game out-of-turn and required my going first. With no specific objective on my part, I played out a game of form C2 in game 7.7 below. After her defeat, Miriam confided to me that when next they played, “I’ll try to get Robby to move here [pointing to cell 6], then I’ll move my B here [cell 7], then I’ll try this trick on ‘im.”
Miriam did not play against her brother till much later, but in session 10 she seized upon Glenn at Logo as a likely victim. In the interim, she had received table turning instruction in the gambit (of game 7.7) and attempted to apply it against me. Contrast these three games:
6;4;2 6;4;31
1 1 A
1 | | C A | | 2 A | D | C
----------- ----------- -----------
7.7 B | 3 | A 10.4 C | 3 | 10.5 2 | 3 |
----------- ----------- -----------
2 | D | 4 4 | | B B | 1 | >
C 2 S 3 C 2
Miriam played Glenn with the obvious intention of defeating him by the C2 expert play. And she got it all wrong! Glenn informed me that Miriam had asked him to open in cell 6 (game 10.4); this is the responding move of the C2 opening game. He moved first; then Miriam in her turn made the initiator’s “opening” move (A in cell 1). This combination is the opening for the side game S3, which Glenn had the knowledge to win. After her defeat, Miriam and Glenn replayed the opening configuration but with her having the opening advantage, and she defeated him. (His moving in a symmetrical variant of his opening counter’s position in the prior game suggests the choice was his. Miriam would have asked him to move in the same location as move 1 of game 10.4). This sequence of games is striking evidence that Miriam had no idea at that time to the significance of opening advantage.
Miriam’s insensitivity to opening advantage was shortly confirmed by her loud thinking. The following dialog (recorded with game 12.3) exhibits this essential difficulty of her play. In addition, it argues that any representation of her tic-tac-toe knowledge at this age must not depend on her attending to or representing her opponent’s possible moves.
6;5;26
1 A
C | 2 | B 3 | D1| 2
----------- ----------
12.2 1 | A | 5 12.3 1 | A |
----------- ----------
3 | D | 4 B | D2| C
S 4 M 2
Dialog of Game 12.3
| Miriam: | My turn to go first? |
| Bob: | Yeah. |
| Miriam: | [moves A in middle]. |
| Bob: | Let me ask you a question. [Placing counter 1 at side cell.] If I move here, can you beat me? |
| Miriam: | It will probably be like the same game. |
| Bob: | The same game as what? |
| Miriam: | The last game. |
| You think it will? | |
| Miriam: | Yeah. |
Miriam’s comment that the two games will be the same is unforced confirmation that she had not yet made a distinction which nearly any other person would see as implicit in tic-tac-toe. It does matter whether one goes first or second; Miriam apparently did not appreciate that fact. With this profoundly non-standard perspective, one which does not recognize the opening advantage of the first player, with her failure to make a distinction which adults assume, her representation was more different from the casual player’s than any casual observer would guess.
Two in a row
Playing with variations of standard games was a common activity in Miriam’s experience. For example, I sometimes played “half a game” of checkers with her (each player had six checkers) and at the end of session 10, I interrupted Glenn as he was introducing Miriam to tic-tac-toe played on a four-by-four grid. Thus, I see Miriam’s following discovery as not too surprising.
Very early one morning (6;8;24), Miriam popped into bed between my wife and me, and by her chatter and playing kept me drowsily awake. She asked first if I wanted to play “Tic-tac-toe – Four in a Row.” I responded that the game was too complicated for me, even before I realized her mode of play was to be marking moves by gestures in the air. When I asked how she could possibly do that, Miriam explained she was envisioning the grid as lines through a series of nail heads visible in the wallboard of the ceiling. “Then all you have to do is make the marks there.” I still refused to play, even “Tic-tac-toe – Three in a Row.”
Miriam continued, “Hey, Daddy, if you play `Tic-tac-toe – Two in a Row,’ the first guy always wins.” I asked what she meant. Miriam explained, “If the X goes first, say in one corner, and the O goes in the opposite corner, the X still has two ways to win, every time.” I asked if she thought anything like that could be true for “Tic-tac-toe – Three in a Row.” “No, it couldn’t,” she concluded.
The next day Miriam agreed to a videotaped session about tic-tac-toe in our home, during which she passed from believing that no such thing as opening advantage existed in tic-tac-toe to producing a crisp formulation of what opening advantage means as it applies to that game: “whoever goes first who knows a good strategy can win.” (Miriam’s formulation of “good strategy” in opening advantage was confirmed subsequently as meaning “a strategy which leads to a fork.”) She did not apparently see the good strategy as one relating an opening pattern and the fork achievement. This crisp formulation is clear evidence that, in one sense, Miriam “knew” what opening advantage means. Her subsequent play is likewise clear evidence that this verbally formulated knowledge had no discernible impact. [Classifying the knowledge as “merely verbal” would beg an important question, the relation of verbally formulated knowledge to problem solving. That question is quite beyond the scope of this study.]
Miriam’s formulation may have had an impact on her play, but there is no way of telling. In games played against herself subsequently, “she” always goes first, but I can claim no obvious effect from the fact observed. An appreciation of opening advantage would incline a person to prefer going first whenever possible, but such a preference is one Miriam owned since first she began playing the game.
Does Miriam’s description of opening advantage indicate the occurrence of a lonely discovery or is this an instance of homely binding? I judge Miriam’s description of opening advantage as an example of homely binding through contrasting it with he “two in a row” insight. In the latter circumstance, literally in the midst of her family, Miriam was intellectually isolated; she could get no one to play the opponent and did so herself. By an accident of elaborating her attempt to make the game simple enough for me to play, Miriam stumbled into a degenerate game where her single opponent’s-move look-ahead was adequate to take her to game end. Her discovery of a determinate win made sense in terms of her understanding of what’s what. That was a “lonely discovery.” In contrast, during the “opening advantage” session, I focussed Miriam’s attention on pairs of games permitting expert wins, the order-free patterns of whose moves are identical, e.g. C2 and S3. Miriam’s verbal formulation of opening advantage seems an observation and thus a consequence of the problem solving situation in which she agreed to be placed. Such an observation should be distinguished from an insight based on her working through a specific problem from her understanding of what’s what. (An explicit and extensive example of such behavior appears in the later section “A new strategy”.)
Speculations
Miriam’s early understanding of tic-tac-toe didn’t distinguish between games where she or her opponent was the initiator. I say she had then a syngnostic perspective, one which recognizes without discrimination what others can see as distinct. Recognition that something so central as order of moves is relevant to play raises a question: is this change so profound as to render obsolete whatever prior knowledge Miriam owned? A negative answer to this question would bear on the importance of the young child’s ego-centricity, noted long ago by Piaget (1926). If the knowledge embodied in microviews is internally represented in terms of one’s own actions (these can be known and controlled step wise), discriminations based on interaction (appearing to the syngnostic perspective as random) come into being as incremental refinements of already established knowledge. Such would help to account for the stability of knowledge based on ego-active, syngnostic perspectives, the progressive refinement of that knowledge, and the adaptiveness of the child’s ego-centricity.
LONELY DISCOVERIES
The inception of multi-role play
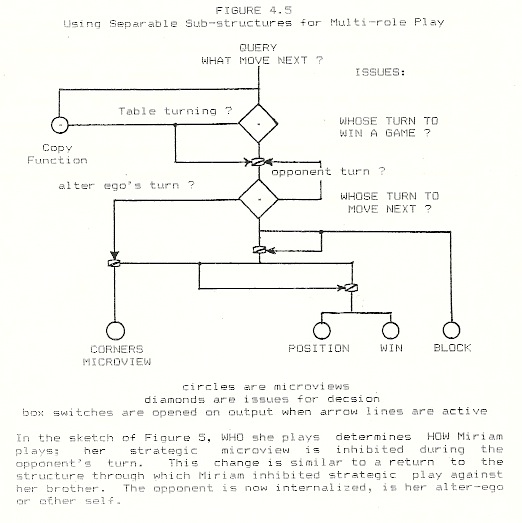
Table turning was effective initially as an instructional mode of play. It became more than that, for Miriam turned the tables spontaneously. After being defeated by Glenn at MIT, Miriam first asked me to replay the specific game and then turned the tables on me. In later games, Miriam went further and incorporated her opponent’s play with her own. It is this skill, simulating another person as an opponent, that is required first to perform the analyses which lead to an explicit understanding of specific games, second, to transfer knowledge from aggressive to defensive play, and ultimately perhaps, to develop an articulate and well-organized understanding of the micro-domain of playing tic-tac-toe.
Playing Robby
Miriam played most games of session 14 against her brother. After an initial tie and a loss to Robby in a corner opening (form C3), Miriam began game 14.3 (below) in a corner. Robby’s opposite corner response (he had successfully blocked her three-corner fork there in all previous play) led first to her noisy complaint…and then this comment, “Robby, you’re gonna kill me for this.” She made an effective crux (defined in Figure 1) for game C1 and continued with a “million dollar promise” that she would not move in cell 4. (I believe she was drawing his attention to cell 4 and egging him on to move there.) After Robby made his forced move in cell 4, Miriam informed him she wasn’t going there anyway. At my question of whether or not she would beat him, Miriam replied, “Yeah, I think so,” and linked her two chances to win into a fork. Miriam honestly beat Robby at a game at which he had been master in all their previous play.
6;6;22
A 1
A | D | C C | | A
----------- -----------
14.3 2 | 3 | 14.4 4 | 1 | 3
----------- -----------
B | | 1 2 | | B
C 1 M 1
In the next game, Miriam invited Robby to turn the tables on her. Robby, not privy to our experiments with tic-tac-toe at that phase, did not share with Miriam the specific meaning she assigned to that procedure. Does game 14.4 show Miriam pursuing a three-corner fork despite the intrusion of Robby’s 3 where a hole should be? Or was it a gift to him? I prefer the latter interpretation because Miriam mentioned to me her surprise that he didn’t know how to turn tables. Such a gift would be another way of alternate winning when your opponent can’t turn the tables.
LONELY DISCOVERIES
The inception of multi-role play
Table turning was effective initially as an instructional mode of play. It became more than that, for Miriam turned the tables spontaneously. After being defeated by Glenn at MIT, Miriam first asked me to replay the specific game and then turned the tables on me. In later games, Miriam went further and incorporated her opponent’s play with her own. It is this skill, simulating another person as an opponent, that is required first to perform the analyses which lead to an explicit understanding of specific games, second, to transfer knowledge from aggressive to defensive play, and ultimately perhaps, to develop an articulate and well-organized understanding of the micro-domain of playing tic-tac-toe.
Playing Robby
Miriam played most games of session 14 against her brother. After an initial tie and a loss to Robby in a corner opening (form C3), Miriam began game 14.3 (below) in a corner. Robby’s opposite corner response (he had successfully blocked her three-corner fork there in all previous play) led first to her noisy complaint…and then this comment, “Robby, you’re gonna kill me for this.” She made an effective crux (defined in Figure 1) for game C1 and continued with a “million dollar promise” that she would not move in cell 4. (I believe she was drawing his attention to cell 4 and egging him on to move there.) After Robby made his forced move in cell 4, Miriam informed him she wasn’t going there anyway. At my question of whether or not she would beat him, Miriam replied, “Yeah, I think so,” and linked her two chances to win into a fork. Miriam honestly beat Robby at a game at which he had been master in all their previous play.
6;6;22
A 1
A | D | C C | | A
----------- -----------
14.3 2 | 3 | 14.4 4 | 1 | 3
----------- -----------
B | | 1 2 | | B
C 1 M 1
In the next game, Miriam invited Robby to turn the tables on her. Robby, not privy to our experiments with tic-tac-toe at that phase, did not share with Miriam the specific meaning she assigned to that procedure. Does game 14.4 show Miriam pursuing a three-corner fork despite the intrusion of Robby’s 3 where a hole should be? Or was it a gift to him? I prefer the latter interpretation because Miriam mentioned to me her surprise that he didn’t know how to turn tables. Such a gift would be another way of alternate winning when your opponent can’t turn the tables.
Playing against herself
In the midst of this interesting situation, I was called away for a few minutes. I asked the children not to play together till I returned. Coming back, I found Miriam had been playing tic-tac-toe against herself, in her words, “making smart moves for me and the other guy.” She showed me her play of game 14.5, where the first player wins after the second falls into a trap of opening C5.
6;6;22 6;7;3
A 1
A | D | C 1 | d | c
----------- -----------
14.5 | 1 | 3 15.1 B | C |
----------- -----------
2 | | B b | | A
C 5 C 1
Attempting later to probe Miriam’s ability to play defensively against a corner opening, I asked her to play as opponent a C1 game (15.1 above). I opened with corner 1. Miriam took over once the chalk was in her hand. (Her subsequent “non-self” moves are shown in lower case letters.) After move B, she paused and wavered, “No. He wouldn’t move there.” I laughed at her attempted cheat and said, “Oh yes, he would.” Miriam made the smart move (c) for her opponent and concluded, “I block him in the center and he wins.” Thus we have a second example of Miriam’s playing both sides of a single game.
The specific game knowledge with which Miriam defeated Robby in game 14.3 was forgotten; that satisfying victory did not permanently affect cognitive structures. In direct contrast, multi-role play (first beginning in game 14.5 at age 6;6;22 and reappearing in the “two in a row” incident at 6;8;24) became a permanent feature of Miriam’s play and one which enabled later significant development. Almost by definition, in the inception of multi-role play we observe that characteristic of lonely discovery, simulation of the role of another, as primary. More importantly, we can see in game 14.5 that Miriam played with her Corners strategy, while “the smart moves” of “the other guy” were precisely the proposals of her own tactical microviews. The ego plays strategically, the alter-ego tactically (game 15.1, initiated by me is the single exception to this pattern in the corpus). The multi-role play appears to be achieved by the splitting apart of two sometimes competing sub-structures under control of a new decision on an old issue, “how do I play this move?” This control element insertion can be seen as effecting significant changes in behavior with minimal changes in structure. The appearance of creating new structure from nothing can be avoided if this new control element insertion is seen as a patch of peculiar power — because it substitutes a particular decision for what had been merely an inhibition in pre-existing structure.
A NEW STRATEGY
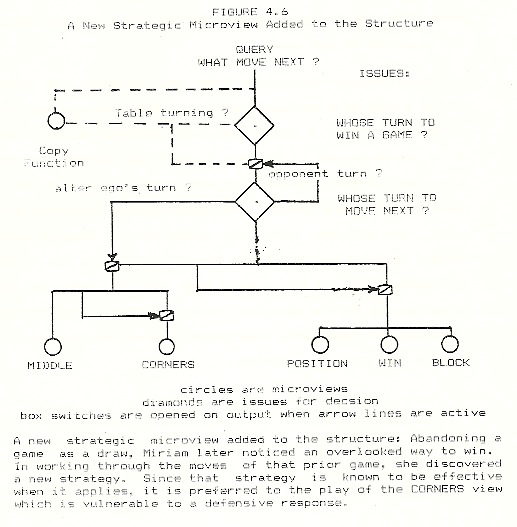
In the years following the core period of The Intimate Study, playing tic- tac-toe lost social currency with Miriam and me. My energies were much absorbed by the analyses and composition of One Child’s Learning (Lawler, 1979). Peggy was born to our family. Miriam couldn’t find a tolerable partner for the game, but this was not a major concern to her for she, as well as I, had other preoccupations. Two sorts of play occurred during this period of relative inactivity. First were the few games we did play (sessions 18 through 21). Second was Miriam’s solitary play and her reflection upon it. From these two sorts of play, two new developments arose: Miriam discovered a strategy different from the three-corner fork; she also became capable of game length prediction (an issue to bel addressed in “A stage change”).
Announcing her discovery
Reviewing her play of the intervening years, Miriam stated that she played rarely and mostly against herself (30 games in two years was her estimate). As I introduced my objective, Miriam proposed one of her own: to apply a newly discovered strategy against me. When I asked her to discuss it with me, she responded, “No way! Then whenever I play you’ll know my tactics.” This more independent stance of hers undercut the loud-thinking openness of our earlier play, but Miriam’s new strategy, which I name the Middle and Corners Fork, is nonetheless clear from her play on the games below and commentary on 22.2:
8;9;21
A A
A | 1 | * A | | *
----------- -----------
22.1 * | B | 22.2 * | B |
----------- -----------
C | | 2 C | 1 | 2
C 4 C 2
| Bob: | [After move C of 22.1] We don’t have to play that out. You’ve clearly defeated me. Masterful. Let’s play another one here. You go back in that corner. That’s where you went the first time…. And I want to try some other places and see if I can get away from you and your new tactic…. I’m going to go down here [cell 8]. That’s the side away. |
| Miriam: | [(Moves B in cell 5]. |
| Bob: | Arrgh! [(Moves 2 in cell 9]. This is a different game. See, I’ve got a way to win…. |
| Miriam: | [Moves C in cell 7] |
| Bob: | Oh no! |
| Miriam: | Careful of your moves, Buster. |
| Bob: | So you’ve got two ways to win now. Let me ask you something. When did you invent this trick? |
| Miriam: | Oh, I was playing with myself. |
| Bob: | Well…. That’s another one for Miriam…. When did you do this? Was it recently or years ago? |
| Miriam: | Recently…. See, what I happened to do. [Here Miriam moves to her desk and returns with a copy of Richard Scarry’s Rainy Day Book…. What I did is I went X. He went O. I went. He went O. |
In a final comment on the discovery of this new strategy, Miriam added that she had played the game and only days later noticed the fork created with her third move. (This comment is born out by the appearance of the original game, where the first six markers are made in brown crayon and the last, the winning move (D) is marked in ball pen.)
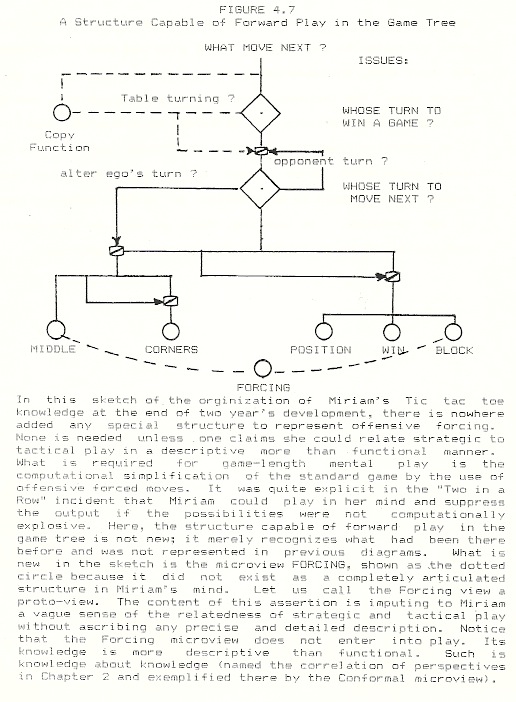
Once Miriam discovered this new strategy, its pattern played a role as a strategic objective, analagous to that of the three-corner fork. I indicate this new strategy as the creation of a new microview in Figure 4.6, where the Middle microview joins the Corners view to form a Strategic Cluster. A striking quality of Miriam’s Middle view play was her certainty of its power. She knew she could win games of C2 and C4 opening forms. This was not so for the Corners view, where the C5 game is indeterminate and (as we shall see) the C1 game had been forgotten and was not mastered. This difference in certitude is indicated by the Middle view’s switching off the output of the Corners view in any competition.
DISCOVERY RECONSTRUCTION
The transformation of this proto-view into the Middle microview occurred during the incident wherein Miriam reviewed and reflected upon the game recorded in Richard Scarry’s Best Rainy Day Book Ever. Let us try to reconstruct the sequence of moves:
circa 8;9
one
original reconstruction another
A A
X | O | O A | 1 | 3 C | 1 | 2
----------- ----------- -----------
* | X | * | B | * | A |
----------- ----------- -----------
X | | O C | | 2 B | | 3
C 4 M 2
(The * represents the way to win Miriam discovered on reflection days after the initial game.) Miriam’s markers do not preserve enough information for a decision as to which fork and interpreted her prior play as the C4 game. After recognizing a way to win she had not taken advantage of, Miriam tried to figure out how she had achieved it. Let us suppose that she attempted replaying in her mind the games below:
circa 8;9
X A A A
X | O | O A | | A | | 1 A | 1 | 3
----------- ----------- ----------- -----------
* | X | - | | | B | - * | B | -
----------- ---------- ----------- -----------
X | | O B | | 1 | | 2 C | | 2
? C 1 C 3 C 4
original failure at 2 failure at C stop at D
(a) (b) (c) (d)
Miriam knew she was on the trail of a good strategy that must fit the constraints of moves of the original recorded game. How could her prior knowledges have helped her discover it? The only other good strategy she knew began in cell 1 and most likely so did her prior play. If in her second turn she selected cell 7, as in (b) above, the Corners preferred cell 9 being occupied, she would have twice missed a forced move (during Alter’s second and third turns); surely she would have thought this unlikely. If Alter’s first move were to cell 3, as in (c), and Miriam’s crux in the center, his response would have been 9. Placing the remaining markers (C in cell 7 and 3 in cell 2) would have required her missing a forced move (to cell 6) and his preferring a pointless cell 2 move to winning. Most unlikely. This second possible game, although beginning in the corner, specifically lacks a three corner objective. Play for both Alter and Ego goes forward by the functions of the Tactical cluster.
The third reconstructed game (d) also goes forward with play of the Tactical cluster. Given the opening move in cell 1 and and Alter’s response in cell 2, the Ego’s next move of choice, proposed by the Position view, was to the center; Alter moved to cell 9 as required. Because the opening response was to cell 2, there was no threat to be blocked; move C is a corner choice such as the Position microview would propose. Move 3 could be explained as Alter’s second forced move. Even if she noticed Alter’s way to win (3-/-2) — which a move D, not made, could have blocked — Miriam’s Ego would not have felt compelled to complete a drawn game. With this last game played out stepwise, with the fork before her, all Miriam needed to appreciate fully her good strategy was to notice that Alter’s moves 2 and 3 were both forced. With such an insight, Miriam could have become master of a fully determined strategy for a specific opening game. She did show such mastery.
In the working out of this specific game as reconstructed, playing both sides according to her documented tactical and game-specific knowledges, Miriam could very plausibly have discovered her new strategy. If so, then her awareness of the individual steps of her own play, in the roles of Ego and Alter, permitted her analysis of a situation most probably noticed “accidentally” by the views of her Tactical cluster. What is most striking about such a situation of thought is that the process (reconstructing the achievement of an objective) not only created a new strategic microview, it also promoted the integration of pattern and serial aspects of play whose long separation I have noted. Now focus on the role of this particular experience in advancing Miriam’s ability to integrate serial and pattern aspects of play.
A STAGE CHANGE
Miriam’s play at age six showed she did not own an integrated understanding of pattern and serial aspects of play. In striking contrast, the final review (age 8;10) of Miriam’s play establishes her ability to work out games in her mind. Multi-role play — originally a social convenience — became a significant cognitive development because it fit a fundamental aspect of tic-tac-toe. [Recall from Figure 4.1 that Expert play requires offensive forcing at the initiator’s second move.] My proposal is that Miriam discovered offensive forcing through multi-role play, experiencing “being forced” as Alter while simultaneously, as Ego, experiencing the offensive use of forcing. Where is the evidence that her very processes of thought changed in quality? If there be such evidence, what light does it shed upon the transition from one mode of thought to another?
Addressing these questions requires we distinguish between exposure to some formulation and the internal processes by which the individual makes sense of what he may have already “known” in a more limited way — no easy task. I address these questions through explorations that revolve around the necessary truth of a conclusion. This focus reflects a central theme running through Piagetian psychology; first, belief rooted in logical deduction is different in kind from belief based on the probabilities of experience; next, when justification by appeal to logic replaces an appeal to experience, a new stage of thought is achieved.
Necessity as a criterion
The central issue of tic-tac-toe session 23 was forecasting victory. Miriam did predict her victory from opening configurations of markers (and prove her judgment correct). Typically, after my opening response, I asked Miriam whether or not she would defeat me and if so, how, as with game 23.5:
| Bob: | Will you beat me? |
| Miriam: | Yes, I think so. |
| Bob: | How? |
| Miriam: | I’ll move here [cell 9], then you move here [cell 5, forced], then I move here [cell 7] and get two ways to win. |
8;10;29
A A A A
A | | 1 A | 1 | * C | | 2 A | * | C
---------- ---------- ---------- ----------
23.5 * | 2 | 23.6 * | B | 23.7 * | A | 23.10 | B | 1
---------- ---------- ---------- ----------
C | * | B C | | 2 B | 1 | * * | | 2
C 3 C 4 M 2 C 2
Game 23.5 joins together in Miriam’s link placement a “forced move” and the three corner fork. In game 23.6, Miriam predicted victory also:
| Bob: | Will you beat me [after move 1]? |
| Miriam: | [a long pause – we may assume she was working out the game in her mind.] Yes. I’ll move here [cell 5]. You’ll move here [cell 9, forced], and I’ll use my new tactic [link the middle and corners fork]. |
In game 23.7, Miriam responded “yes” to my prediction question as she wrote move B, and continued, “You’re forced to move here [cell 3] and I get two ways to win.” She was uncertain about whether or not she would win the indeterminate games of form M1 and C5. Miriam paused long before answering that she would win game 23.10 and objected to my even asking her the question because she was “trying to think.” Once she did give her judgment about victory, Miriam admitted she had the complete game worked out in her mind.
At the end of the study, Miriam had achieved that phase of procedural comprehension mentioned earlier and exemplified most fully here. Notice that her uncertainty in the indeterminate games is both appropriate and supported by her fragmentary comprehension of the specific game C5. In game 23.10, when she said I would move 2 in cell 9, I objected. Miriam countered that I had to move there or she would win directly. There can be no clearer indication that she was using offensive forced moves both in mental play and in the justification of a victory claim. (This does not imply she had crisply formulated and used for guidance a general principle that the crux must force the opponent’s second move out of the way of the planned fork.)
We have used the stage change criterion of a qualitative difference in thought to support the claim that Miriam exhibited some significant learning, but that does not necessarily commit me to adopt, ultimately, a stage theory. This is especially the case when one aspect of my endeavor is to explain stage changes as emergent saltations in behavior from incremental changes at the micro-structural level.
How did Miriam learn about the use of offensive forcing? There are at least three obvious candidate answers to the question. First, it is possible that someone told Miriam everything she knew. Alternatively, she may have figured out everything herself (regardless of whatever cultural presses existed). An intermediate position is that someone told Miriam what’s what (which objects or categories of things are important) and that subsequently she was able to figure out what follows (what categorical and functional relations obtain between those highlighted elements). [But such a position raises immediately the question of how one explains how a particular bit of advice comes to function with power in thought.]
Miriam’s corners strategy was long preceded by the slogan “look for two ways to win,” and the earliest sign of her sensitivity to other forks and attempting to achieve them occurred two years prior to her working out of the middle and corners strategy. We should not be surprised if Miriam took from my instruction the notion that there might be such a thing as offensive forcing and later, alone, discovered situations in which the relation applied with power.
We can not exclude any of these three possible interpretations of this incident. Miriam could learn both by instruction and by creative problem solving. As in the incident of her introduction to the three corners strategy by Robby, it is clear that instruction was best absorbed when it was a response to questions she herself posed. I explicitly told Miriam, in discussing game 20.4, that what was required for expert play was “forcing the other guy’s next move out of the way so you could get your two ways to win.” Even though, consequently, she might have learned offensive forcing from me, that instruction was my lesson and not one she provoked with her own questions. In the earlier “Discovery reconstruction,” I traced in detail a plausible sequence of problem-solving moves as a result of which Miriam could have not only discovered her new strategy but also experienced “being forced” as Alter while working out a win for herself as Ego.
I choose to believe that Miriam learned as described in “Discovery reconstruction,” even though my family and my experiments functioned as an intrusive didactic system. The interpretation is not established, but the possibility of such learning, in a nearly computational description, is established by the analysis in this particular case. Maybe that’s enough. No one need be ashamed to admit that people can learn through being taught (how, precisely, those lessons might be internalized is a major technical problem once one admits any complexity to the structure of the human mind), nor to admit that some people learn this or that, according to their own objectives, from what other people do and say (techincally a more tractable problem than the former) so long as all recognize that all people can learn from what they do (once we admit that control of learning is within the mind of the learner, this may be the easiest, technically, of the three problems to describe and model).
The functional lability of cognitive structures
The criterion for the qualitative change in Miriam’s thinking is that she showed herself newly able to predict and prove claims of victory by forward mental play in the tree of possible games. If Miriam discovered the use of offensive forcing as portrayed in “Discovery reconstruction,” this stage change which her ability to prove game outcomes implies must be seen in a new light, as no more than (and no less than) the application of structure developed in one task to a second related but different task.
The task is different because the balance in use of the structures is different. Proposing a move permits reactions as well as reflection. In contrast, proving a victory begins from limited input, has a different output, and requires thought in a more deductive mode. Miriam confronted this new task only because it was presented forcefully to her by her society in the person of me, her father, functioning as psychologist. We should not be surprised that a small change in a system of cognitive structures permits it to cover a new class of related but distinct problems if we take seriously the idea (presented crisply in a limited context by Sussman, 1975) that the mind functions as a closed system, doing the best it can on problems beyond its capability by deforming its interpretations of the problems into little more than minor variations of others it has solved before. Miriam’s working through the puzzle of how she achieved the fork in the discovery incident gave game-length mental play a significance she could appreciate. Once this major extension to game-length mental play had been established, the next step, to answering predictive questions, was a small one to make. The incident wherein this new capability emerged was essentially private and different in character from its first public manifestation. Such functional lability is the hidden power which gives effect to lonely discoveries made through the accidents of application of already existing ideas to new problems. Is learning, then, any more or less amazing that the evolution of flight or the invention of writing?
CONCLUSIONS
I have applied a vision of the interaction of social experience and the personal construction of knowledge in the interpretation of a corpus which spans a period of significant cognitive development in one child’s learning about a single task environment. This chapter presents in considerable detail a particular path of experience and structural change which constitutes a worked example of how a “stage change” in task-domain performance could emerge from the incremental elaboration of local clusters of knowledge. One striking result is that simulating an opponent with pattern-driven, ego-activity-focussed microviews can lead in simple steps to that mature mental play described as “forward search in the game tree of possibilities.” The separability of the tactical and strategic modes of playing tic-tac-toe, reflected in cognitive structures, permits the simulation of an opponent to develop for interactive mental play. The wealth of fragmentary knowledge acquired in situations of homely binding permitted Miriam to work out in private a new strategy — itself a creative application of imperfectly comprehended experience. I have proposed, with reasoned though not coercive argument, that the working through of this new strategy also entailed development of that progressive mental play which permits prediction and proof of outcomes from openings — an advance in behavior which could be seen as so significant as to mark a “stage change.”
I began by admitting that tic-tac-toe is generally considered a trivial game. Now it seems more appropriate to ask and answer a deeper question: “Given the simplicity of information processing descriptions of mind, how is it possible that one could learn so complicated a thing as tic-tac-toe at all?” The first answer is of a computational sort, in the sense that fragmentary specific game knowledge enables insights which simplify the exploration of possible paths of play. Further, we have seen that the structure of the game permits the separate development of different ways of playing, each embodied in a relatively self-contained substructure (microview or microview cluster). The separability of these substructures, which once separated could be assigned roles in the turn-taking structures of behavior that we have all practiced since infancy, permits ego-active knowledge (as in Miriam’s first strategy) to be extended first to ego-with-controlled-alter knowledge (witnessed in her multi-role play), finally, as we may imagine, to knowledge of interaction as such. The answer is, in short, neither purely psychological (depending on the developmental processes and structures of information in the mind) nor entirely epistemological (dependent on the structure of the game), but rather it resides in the synthesis which is that of the mind interacting with things of the world.
Tic-tac-toe stages
I earlier discriminated four stages of tic-tac-toe comprehension. Naive comprehension characterizes Miriam’s play at the beginning of the study, where her play was guided by propensities or by the three-corner objective when devoid of any sense of how to achieve it regularly. Fragmentary comprehension is quite clearly exemplified in Miriam’s highly specific knowledge of the two outcomes of game C5 (corner-middle opening). Procedural comprehension is exhibited by Miriam’s later proof of victory predictions. A systematic comprehension is witnessed by the view of tic-tac-toe presented in Figure 4.1. Miriam never got this far. Let us now step back from the detail of the study to observe how transitions between these four stages of play relate to the articulation of complementary roles and to the processes of homely binding and lonely discovery.
Miriam’s inventing of her middle and corners strategy, a central event in her transition to procedural comprehension, is a case of lonely discovery. The sense of a casual mulling-over of previous activity in our reconstruction of the discovery incident recalls William Wordsworth’s observation that `poetry is passion recollected in tranquility.’ My formulation echoes his:
Understanding is a description of experience articulated through reflection.
We may choose to say that both systematic and procedural comprehension are forms of understanding without doing violence to the common sense of the terms — but it would stretch that use unacceptably and with little purpose to include under that term Miriam’s initial propensities and her fragmentary comprehension, as of specific games. Thus we set the watershed of understanding between fragmentary and procedural comprehension.
The major transition
The main question to ask, then, is how the transition from a fragmentary to a procedural comprehension occurred. If the essential insight in Miriam’s middle and corners strategy is the necessary relationship of the crux and the fork, what is implicated is a revision of the idea of forced moves so that they are seen as offensive tools as well as being threats to which a defensive response must be made. What was behind this discovery? I believe the transition came in multi-role play where Miriam could feel herself “being forced” as simulated opponent by the crux she herself placed as initiator. This insight occurred as a lonely discovery, but its social underpinnings were both pervasive and manifest. Multi-role play grew out of table turning and a second practice: my permitting Miriam to specify what moves I should make. The question of predicting victory was much a research question; but it also was more, with a significant personal and social component: I don’t like condescending. This salient question in our play must have sensitized Miriam to the issue of necessary connection between crux and fork. Even if the transition to the progressive level of comprehension was a lonely discovery, Miriam’s fragmentary knowledge was very much the fruit of extensive social engagement – beginning with Robby’s introduction of the three-corner fork through that multitude of games from which C5 emerged as one opening of well-known outcomes.
The first transition
We can also ask how Miriam moved from the propensities of naive comprehension to fragmentary comprehension. With her first uses of the C5 opening ploy, initially there was no sense of the opponent’s role at all. The distinction between the winning and tieing outcomes was socially driven. Without her attending to forced moves, “tolerable” mature play would have been impossible. The idea of defensive forced moves is the socially determined sine qua non for initiation and play as an independent player. Without command of forced moves, the game is random and unacceptable to an opponent such as I; thus, to play with me, Miriam had to endure instruction. The squabble between Miriam and Robby in session 2 is more evidence of the social pressure behind this original transition.
The final transition
Since Miriam did not develop a systematic comprehension of tic-tac-toe, one can’t ask of this study how such a transition happened – unless he is willing to admit as relevant how it happened for me, to take as admissible evidence my reflection upon the entries of a journal I kept during The Intimate Study. Let me sketch my conclusions from reviewing that material. My comprehension was first, at best, procedural. As we two played, I was uneasy with my own ignorance. How could I understand Miriam’s play without a solid grasp of the material? I found it too hard to comprehend an ongoing game and its possibilities in terms of thinking of some set of simple rules. Privately, I began tracing out “chances to win” to improve my grasp of the game – and found this a dead end. I began playing against myself. [These games and notes about my formulations were kept in a private journal, separately from The Intimate Study.]
First I played a C3 game to a tie – then found that with the crux in cell 9 I could have an expert win. Next a C1 game followed the same pattern: first I played to a tie, then, doing something different, I discovered an expert win. With games C2 and C4, I went immediately to expert wins. I also found one for the S3 game (but not S2). Now aware that there were so many expert wins, I decided it would be useful to classify them to support my recall and to suppress confusion. Here I realized that a classification by the two opening moves was adequate. A further note, supporting the arguments advanced in the discussion of session 22, is that the forms of winning games I initially developed were the same as Miriam’s middle and corners strategy. I later abandoned the initial “hard” solution for the “harder” expert wins of Figure 4.1 because this permitted the use of a common crux for the four games C1-C4. My concern with this “trivial game” was for me unusual, and driven by my social engagement with Miriam. Because I owned a higher standard of performance for myself (and had a need to achieve it) than was possible with my initially syngnostic perspective on the game, I constructed a richer and more controllable perspective through a process of lonely discovery based upon articulating the complementary roles of the game.
Our final formulation then is that:
Understanding is a description of experience articulated through reflection.
You may ask “Is that worth the effort?” I respond with the rhetorical question, “Is understanding worthwhile?” and conclude that if we understand better what we “knew” before, that is significant learning.
Publication notes:
.