LC1aA3
ZOOM – a Logo language interface
ZOOM is a Logo language program written to introduce novices to both turtle geometry and the experience of programming. It is a Logo language and turtle geometry interface whose purpose is to provide a rich experience of the domain (turtle geometry) while permitting a gradual development of programming knowledge.
By a rich experience of the geometry I mean one where each action has an immediate result, usually perceptible immediately (penup and pen down are not so); where experiment is very easy and mistakes are not forbidding. Within ZOOM, keyed entries are single characters, (the exceptions are program names and operand values). The capabilities of ZOOM are two: basic operation of the turtle (forward, right turn etc. ) and program generation from a list of previously executed operations. Programming knowledge will develop in four phases.
Introductory Phase
There are two simple steps. First is use of the letter C to clear the display. This is a command to the computer and not an erasure-like action ascribed to the turtle. The second step is introducing the four operations of the geometry: forward, back, right turn, and left turn. No operands are used for the four operations. The turtle zooms ahead or back a fixed distance; he turns right or left through a fixed rotation. These operations, executed in whatever orders the novice chooses, will give him a rudimentary feeling for the primitives. The clearing operation makes any mistake correctable by re-executing the preceding operations. The conclusion of this phase is with familiarity of the four operations and the clearing command to the computer.
Remembering Things Phase
The first class of items the novice instructs the turtle to remember are the operations penup and pendown, viewed as remembering to keep the pen up and remembering to keep the pen down. The second class of items for the turtle to remember are resettings of the default operands for the geometry operations. Specifically, the character T produces a statement that the turtle turns so many degrees and a request for a new value for the operand The character Z produces a statement that the turtle zooms so far and a request for a new value. The purpose Served here is the introduction of an intermediate unit (of variable size) with a perceptible value. In contrasting this unit, which can be perceived by and is thus meaningful to the novice, with the degrees and turtle steps , the latter units, of no apparent meaning, can be rendered meaningful and the numbers required as operands for the basic operations can be explained as required by the turtle’s different sense of ‘how much of a thing’ matters.
Remembering How to Phase
Programming, within ZOOM means “the turtle’ s learning a name to call all the things he has done since the last clearing command”. Programs are useful to the turtle (and the novice) so that he can remember what he has done and do it again any time the novice wants him to. Once someone has pushed the keys 48 times to make a 24 sided ‘circle ‘ , he will want to save himself that trouble in the future. Fascination with the ability to creates a figure by giving a name, as contrasted with additions of keying, leads to proliferation of that figure and directly to super-proceduralization.
Reflective/Analytical Phase
Once a session with ZOOM has ended, an examination of the programs generated will show the following:
l. the relative simplicity of super-procedures (the ROSE made from the CIRCLE will have many fewer statements than the procedure for the CIRCLE.
2. the repetitive operations generated by key-pushing can be simply reformulated in two ways:
-
a. if a box has been made 60 units on a side by a sequence of 6 FD 10 operations, the meaning of FD 60 can be rendered very clear. The justification is that it’ s easier. One may think of this editing procedure as correcting the mistakes of another (the ZOOM program) or as a kind of definition of what a programming operation is: doing or repeating some small unit of action until you’ve done it as much as you want to. This is condensing a string of identical operations through summing the operand values.
b. the generalization is from condensing a string of identical operations to condensing couples of operations, e.g.. FD 10, RT 15, as units of programming. It is through this generalization that the power of subproceduralization is revealed.
When the novice has progressed this far, he is no longer a novice but a neophyte and well on his way to becoming a computer cuckoo. He can explore turtle geometry with a triple foundation to his understanding:
l. the distinction between operations and operands
2. a translation from units meaningful to him to units meaningful to the turtle.
3. an understanding developed through concrete experience of the power of hierarchical proceduralization.
ZOOMing with Robby
After I had written the preceding text, my son Bobby, aged six years four months, spent four days with me at Logo. The Children’ s Learning Lab served as a home base whence we made excursions in the Boston area. Bobby spent a half day or more at Logo each day and during those times played with whatever available toys his will directed him to: sometimes the tinker-toys or the multi-way rollaway, sometimes drawing with crayon on the back of abandoned terminal printouts and, of course with the Logo computer system.
Robby, making brownies with Seymour
The examples at the end of this paper show some of my preconceptions of how one might get into explaining the ideas of the preceding text. And we did step through that exercise eventually (Bobby was that generous with me) , but not until several days had passed…. for Bobby had his own ideas .
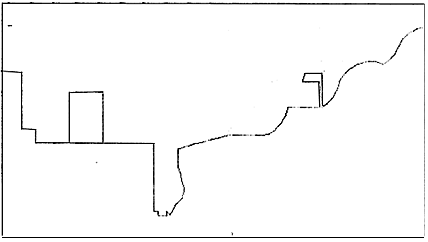
When we first entered the Learning Lab, late of a Sunday afternoon, Bobby saw Henry Minsky, a Logo person about twice Bobby’s age, executing his Lunar Lander programs. The visually striking aspects of the program execution are the drawing of a moonscape (with cliffs, a building, a canyon, etc. . ) and the use of the display turtle to represent the landing vehicle. Bobby decided he wanted to make one of those.
After logging in, I explained that we could run a program I knew, called ZOOM, that would make it easy for him to draw pictures; that the way to run the program was to tell the computer the program’ s name, and that we spoke of this as “invoking” a program. ( Here I was trying to give Bobby the conventional name for the new procedure he was learning so that he could refer to the procedure and talk about it. Bobby typed in ZOOM and carriage return.
When we printed out the instructions, he said I would have to read them to him (a half page printout is imposing to someone who is working on reading one sentence at a time) , but he didn’t listen when I read them. We kept the list by the terminal for later reference. Forward (F [FD 20] ) and right (R [RT 9O]) and clearscreen (C [CS]) is where we started. But there was a problem right away; Bobby’s plan called for starting at the upper left edge of the display with a clear screen. The turtle started at the center of the screen and drew a line whenever he was moved.
This is where the fundamental difference in our objectives became clear to me, Bobby wanted to solve that particular problem; I wanted him to develop a way of thinking about Logo operations and programming. It is in trying to bridge this gap that anthropomorphization is so useful. One can think of learning the Logo operations and their programming as like learning what kind of creature the turtle is. This is useful because what the child knows about himself can be points of connection about which questions can be raised. For example, in solving Bobby’s problem, after looking at the pen mechanism on the floor turtle and explaining how it could be up or down and explaining how you can tell the turtle where it should be, I was able to raise the issue of whether the turtle would forget to keep his pen up if he got busy doing the other things we wanted him to do. Bobby and I forget, but the turtle doesn’t; he remembers very well. The process this example represents is this: a frustrated objective becomes a particular problem; solving that particular problem involves looking at the mechanism of the system; the language in which you discuss the particular problem, to the extent it makes contact with what the child knows, permits his formulating the solution (and reformulating the particular problem) within a developing framework that has systematic properties, e.g. turtles remember very well what you tell them, . . .even if people don’t.
When Bobby got the display turtle to the edge of the screen, he began to draw quite happily. He made a cliff, a landing site, a building. . . . and developed a problem: the width of his building (20) was the smallest unit of distance he could command the turtle to move So he was unable to make any windows. (Henry’s building had windows.) He let the problem slip by and went on to draw another cliff going down into a canyon. His dissatisfaction became very clear. He wanted to make some tiny rocks at the bottom of the canyon and asked me how to do it. I warned him that it would be a very long explanation and asked if he really wanted to know. He did.
I was pleased, for one of my subordinate objectives was raising the issue of the units of things and how they relate to number. He played turtle. “Forward”, I said. Bobby took a step Forward; another step. “Forward”, I said, ”Two steps.” “Do you have to tell the turtle how many steps to take?” We went to a different terminal, not using ZOOM, but connected to the floor turtle . I keyed [FD l] and the turtle twitched. “Did he move ?” “Yes, Dad, but he didn’t go anywhere.” [FD 100] I next keyed in. Bobby came back and took a look at the terminal printout. He said that 100 steps didn’t take the turtle very far. The conclusion was clear that turtle-steps were tiny. I introduced that specific name at that time. Back at the display running under Zoom, a single character [F] left a 20 unit line. I admitted that I had told the turtle to remember to go 20 turtle-steps every time we said forward. “How far can you go in 20 steps, Bobby ?” Bobby paced off twenty steps and from the hallway noted that turtle steps are tiny. At this point I told Bobby the program was called Zoom because when you say [F] , the speedy display turtle zooms forward however many turtle-steps you told him to remember.
We went back to zooming, and I showed Bobby how to change the number of turtle steps the turtle should zoom. After making a few rocks, Bobby went over to look at Henry’s moonscape and came back puzzled. He wanted to make a “slope-y’ line but the turtle always made Square corners. How can you explain to a child what 9O degrees means ? Bobby had seen the display turtle turn through 90 degrees when he commanded a single right [R]. Playing turtle, he and I made 90 degree turns . I said when I turn, right or left, that’s how much of a turn that matters to me. “How much of a turn matters to a turtle is different. Much as the turtle makes tiny turtle steps too small for us to see, he makes little turns, called degrees, much smaller than our turns. When we want the turtle to turn, we have to tell him how many little turns we want him to make. The number 90 meant very little to Bobby. He could say the name but he no idea what to make of it. He asked what was a good number to use for making slope-y lines. I told him 15, which he remembers well. Knowing that 90 degrees make square corners and 15 degrees make good slopes, he is bound to ask himself about the numbers in between. I was more lucky than well organized in finding the question of units arising first in the linear rather than in the rotational dimension. I was lucky because it seems easy to connect the idea of tiny turtle-steps to a child’s experience. Inducing the idea of a small turn might be harder for a child. But, having done the first, the extension of the explanation to the rotational case was easy.
The next problem we encountered was a big one. Bobby started making his slope-y line and got carried away with it; the line carried the drawing to the far edge of the screen in an uninteresting way. He wanted to get rid of the part of the line he didn’t like. The display system doesn’t let you do that. “Oh Brother!” Bobby cleared the screen and replicated his earlier work to his own satisfaction. I stopped and asked, “Suppose you make another line you want to get rid of ?” Bobby maintained he would be exceptionally careful. I told him I knew a good trick we could use so he wouldn’t have to be so careful – making a program. “What’s a program ?” It’ s telling the turtle how to do something (That’s the programmer’s view of it) . We had made the turtle remember things: to keep his pen up; how many turtle-steps and degrees he should zoom or turn. A program is remembering how to do something. (That’s the turtle’s view of it) . How do you make a program in zoom ? You key the letter “P” . Bobby did that. The turtle asked the cryptic question ” Program how to what ?” Bobby read the question but was puzzled. I explained that when the turtle remembered how to do things, he needed to know what name you gave to doing that – so you could tell him later when you wanted him to do it. Bobby declared his work was named “big building” and asked how to spell it. ”b-i-g-b-u-i-l-d-i-n-g” . He asked if we could call it something else. I answered that if he could remember what he called it, the turtle could remember too, so any name was good. ”BB” was chosen. The program was created and the turtle claimed he would remember how to “BB”.
The next step (and the immediate one for which the program generation was a preparation) was a tricky one . Tricky, because it depended on Bobby’s trust in what I told him would happen and because his work, the display drawing on which he spent the past hour and a half, was at risk. I told him to clear the screen. He did it. ”Do you think the turtle will remember how to draw your big building ?”
We returned to the new word in his vocabulary, invoke. I explained that if you tell the turtle the name of a program, he will execute it. Bobby invoked “BB” . He was surprised and utterly delighted when it worked. From this point on, his work was considerably less at risk. He could make a checkpoint anywhere and continue from there with only the newly keyed commands needing re-entry if he changed his mind about his intentions. Bobby continued from that point to create a moonscape of which he’s very proud.
Robby’s Big Building (procedure “BB”)
There were other developments over the next few days . Dissatisfied that his building had no windows, Bobby decided to make a separate building and put windows in it . His separation of the entities “window” and “building” seemed a good opportunity to introduce the idea of subproceduralization. I suggested he draw a window first, then he could tell how big he should make the building. He followed that direction and we worked together on getting the windows into the building. Bobby has had an experience of using subproceduralization, but I do not believe he has seen the power of the idea. (One direct reason is that the cumbersomeness of commanding the turtle to move to the locus for the window overwhelmed the sense of simplicity in creating a window with a name.
We played with the floor turtle several times, and Bobby decided to draw a building there. Well and good. We spent some time figuring out the change of scale, what would be the best number of steps for the floor turtle. When Bobby was all set, I asked him where the building was going to go. For the first time in my life, I saw him construct beforehand a very specific plan. By specific, I mean detailed to the point of writing down on the paper: “floor here” three times with arrows pointing to the target location; “roof” three times at the far edge of the paper; a line of arrows showing where he wanted one of the walls; and an “S” to mark the beginning point for the building. Having discovered how to make a building in the Logo language on the display system lead him to planning in a domain superficially different but with the same operations. We might consider further exploiting the functional isomorphism of the floor and display turtles.
The final development was my attempting to wean Robby from using zoom (It’s intended use is purely introductory. ) . With the previous discussion of ‘how much of a thing matters ‘ to the turtle, I tried to explain the operation/ operand structure of commands. “we also spent time examining programs Bobby had caused zoom to generate. I tried to relate for him how [FD 20 FD 20 FD 20] is the same as [FD 60] ‘ . . and use this to explain what addition is. (Bobby can add some of the low numbers [and two digit numbers ending in zero] ) . I believe he understood.
Worked through in two or three long sessions and a few short ones this experience with zoom was a productive mini-course for both my son and me.
Publication notes:
- Written in 1976. Unpublished.
- 1986. Subsumed in “Three Encounters With Number” in Cognition and Computing, Lawler, DuBoulay, et alia, John Wiley.
After Thoughts
The story above took place when Rob was six. Another six years later when he began to use the new Apple Sprite Logo system, the first project undertaken was the reconstruction of the moonscape first made with ZOOM.