Vn128.1 Robby’s Topological Game 4/2/78
About a month ago, Robby was shown a paper-cutting game by a
classmate’s parent. The procedure to follow was this:
1. Cut two paper strips of equal length (8″ will do)
2. Draw a line down the middle of each (using lined paper makes
this unnecessary)
3. Bend each strip of paper into a circle and tape the juncture
4. Join the circles perpendicularly and tape the juncture
5. Cut around the mid-line of each circle.
When two strips of equal length are so connected and cut, the surprising
result is that, though having passed through a circular phase, the strip
halves end up taped together as a square.
Robby enjoyed this game when shown it. Yesterday, I removed
a paper form he had made in the past (an 8 x 11 sheet divided into 11
strips 8″ long) from my clipboard and gave it to him. When I inter-
rupted his reading to give him this sheet of paper, Robby recalled the
game and quietly took it up on his own. He was very happy when the
procedure produced a square and showed it to Gretchen and me. We neither
paid much attention.
Going on to three circles, Robby cut two of the three along
their mid-lines. He judged (in error) that he had finished by finding
a square with a bar (a double strip) across the center. It lay flat.
Still no one paid attention. Robby went on to four circles, and he
cut all the mid-lines. What he got was a confusion of floppy paper.
I advised him to try to get it lying flat. Robby again borrowed my
clipboard, clipping and taping the product to it. He was delighted
when he succeeded in flattening the strip-figure and subsequently
taped it to a large piece of cardboard. The resulting shape is this:
But why stop at 4? Robby went on to connect and cut 5 circles. Here
he met another surprise. When cut, the 5 circles separated into
identical, non-planar shapes. Robby likewise taped these to another
piece of cardboard. When he made a cutting of 6 circles, controlling
the floppy strip-figures became a big problem. Robby succeeded at
taping it to the box from which he had been cutting cardboard backing
pieces, but in doing so went over an edge. He decided the problem
was getting too complicated to be fun and quit.
This morning I told him I had been thinking about his paper
cutting game and asked Robby to find the figure made from three circles.
When he returned, I asked him if he had cut all three circles. Robby
thought so, but when I pointed out the middle bar in his square was
double thick, he agreed he had only cut two. Robby saw immediately
that his square would divide into two rectangles. He cut the center
strip. “The 5’s made 2 too. Hey! I’ve got a new theory: the odd-
numbered circles make 2 and the evens all stay together.” I agreed
that this was an interesting speculation and that I could believe it
might be true, but that I couldn’t see immediately why it should be.
Relevance
I see this incident as one exceptionally valuable for
characterizing how significant learning occurs very naturally in a
mildly supportive milieu. First note that the initial exposure to the
“phenomenon” was quite memorable and puzzling. (How can you make a
square from two circles?) Robby clearly marked this phenomenon in his
mind as one which he would explore later. This pending explorarion was
invoked by the accident of his seeing a piece of paper approximately
meeting the material requirements for use in the game. The circum-
stance was one of no pressure. (He had been reading all of Gretchen’s
collection of Oz books and was probably a little bored.) He had no
outside direction or motivation at all. Once Robby succeeded at
making a square, he continued executing the procedure with stepwise
complications all focussed on one variable — the number of circles.
(He might have chosen to make the strips of different lengths — a
possibility he mentioned.) With the 3 circles, Robby stopped prema-
turely because he had produced a result (a square with a bar) only a
little different from the next simpler case (2 circles make a square).
With 4 circles, the outcomes of cutting were apparently sufficiently
confusing that completion could not be judged from the product but
depended on verifying that individual steps of the procedure were
completed. With the figure of 4 circles he was excited and delighted
to have succeeded in imposing some sort of order on the tangle — and
that the final product showed a family resemblance to the earlier
products. Finally, Robby was quick to jump to conclusions (his new
theory) in explaining why some figures were connected and others were
not.
Post Script — 4/3/78
After writing the preceding, I spoke to Robby again of his
game and his theory, inquiring whether or not he could prove it correct.
His method of choice was to test the case of 7 circles (which, as he
later found, splits into two planar figures of overlapping near-squares).
I tried to introduce the idea of a proof in place of another case study,
suggesting he take all possible cuttings of 3 connected circles and
figure out which one cuts the strip-figure in half. He said he had cut
the center first one time and at another had cut from one end.
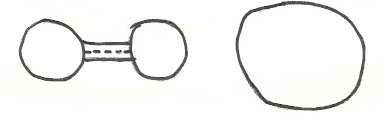
Robby then drew the two pictures below on my chalk board:
He argued that it is always the last cut that severs the strip-figure
in two, representing the situation as at the above left. By cutting
along the dotted line, one joins the two small circles (here he made
motions of pulling apart the strip pieces) into the one large one.
Note well that this argument is merely a restatement of how he
appreciates the deformation, but it contented him.