LC1bA3 ^
SKETCHES OF NATURAL LEARNING
In a famous passage of the classic The Sciences of the Artificial (1), Herbert Simon describes the complexity of the movement of an ant across an irregular bed of sand then concludes:
An ant, viewed as a behaving system, is quite simple. The apparent complexity of its behavior over time is largely a reflection of the complexity of the environment in which it finds itself.
He then asserts his objective of exploring this hypothesis — but with the word ‘man’ substituted for ‘ant’. Simon, and his colleague Newell, have pursued this vision with vigor and precision, doing their best to represent apparently complex human behaviors with architecturally simple computational models.(2) Their architypical analysis is that of a mature person solving some variation of one of Bartlett’s cryptarithmetic puzzles; the analyses are exquisitely detailed. Their colleagues have worked for 15 years to extend this vision to a broad spectrum of performance on psychological tasks. Some of us remain unconvinced of the correctness of Simon’s vision despite this admittedly impressive corpus of work.
It is possible to imagine that through experience people construct internal models of the world and that the details of these models and their interrelations may come to be more complex and more effective in determining behavior than their external environment. The simplicity of manifest behavior witnessed in the problem solving protocols analyzed by Newell and Simon may be a consequence of a highly developed self-control of mature subjects — a characteristic of behavior rather different from the volatility of the child from whom every adult grows. The following example, from Midwest and Its Children (3) may be taken as representative:
from Midwest and Its Children (Barker and Wright)
On June 2, 1949, four year old Margaret Reid spent 28 minutes in the Midwest behavior setting, Home Meal (lunchtime)…. Her behavior was consistent with the standing behavior pattern of the lunchtime setting.
But this is by no means all. Margaret did 42 clearly discriminable and different things on the level of behavior episodes during the 28 minutes.
Here are 21 of the 42 actions, just half the total:Rejecting lemonade; Recollecting pancakes eaten for breakfast; Cutting tomato; Helping self to noodles; Forecasting Bible School picnic; Challenging little brother to lunch eating race; Appraising combination of lemon juice and milk; Inquiring about Valentine’s day; Coping with dropped napkin; Commenting on play of neighbor friend; Playing on words about Bible School picnic; Wiping something out of eye; Reporting little brother’s capers; Dunking cookies in cocktail sauce; Telling about imaginary friends; Putting box of Kleenex on bench; Inviting parents to look into stomach; Soliciting mother’s opinion on brother’s eating;Using spoon as airplane; Chanting ‘Bones to Be, Bones to Be’; Reporting on birthday greetings at Bible School….
Barker and Wright then expand one of these incidents — Cutting Tomato — into fifteen even more detailed action descriptions. How information processing models of today should approach material exhibiting such volatility is far from clear.
There appears to be a lot going on in the human mind. How that multiplex activity relates to problem solving ‘in the wild’ (as in the mind of a child) may be critical to understanding natural learning.
The Organization of These Sketches
This collection of observational material is grouped under three headings:
* Complex Minds and Homely Circumstances
* The Character of Natural Learning
* Instruction as Invention
The sketches themselves are drawn from a collection of protocols of my son’s behavior either at the MIT Logo Laboratory or elsewhere in my presence. (4) At that time, the MIT Logo Project was in the vanguard of Educational Computing research. With the broad diffusion of microcomputer in schools, these observations are now more widely relevant than when originally collected. Much of the material was mechanically recorded, manually transcribed, and collated with its appropriate documentation. I present here the more interesting extracts from that larger and more detailed corpus of material.
I believe this material is relevant to studying learning directly, in that the examples can illuminate the character of learning through problem solving; further, the observations also highlight the methodological problems of studying learning. Finally, the examples of developing new activities and experiences to advance learning, based on the particular experiences of individual children, suggests that this may be the area in which the computer, as medium, may ultimately have its most profound effect on education.
COMPLEX MINDS AND HOMELY CIRCUMSTANCES (5)
Guests coming to our house one day inspired my wife to bake a Rum Cake, a favorite dessert of mine. The children knew that with company around they could take advantage of our playing the role of tolerant parents – and they did. I will mention, but not recount, the noise and the various rambunctious exhibitions before and during dinner and now proceed directly to dessert – for that Rum Cake had seized the children’s imaginations.
We all had a piece. Afterwards, I, with my cigar and glass of port in hand,had to admit that the children might have a second piece of cake. Andeventually when, in pajamas, they claimed a third piece of cake, I made the best defense I could, agreeing to this third as the last piece; declaring (after the fact) that each could have three, I argued that they had had pieces number three, number two and one, and that only zero was left, no more. Thus, when finished, off to bed they must go. After a few bites, Robby excitedly countered, “We can have a million more pieces”. He elaborated by explaining that there were “a million numbers less than one”. I asked what he meant. “There’s one and zero.” Robby replied, “Then there’s zero minus one.” “And what else ?” I queried. “Zero minus two.” “That’s two,” I agreed. “And minus five, and minus one hundred…and minus one million.” This completed his proof.
Robby had been introduced to two particular negative numbers before (6). I infer that in the few intervening days(if not at the moment of this little episode itself) Robby had invented forhimself the negative integers as symmetric to the positive. His excitement, as we discussed this trivial occasion of pieces of cake, showed his engagement with this aspect of the number system.
Family Customs and Knowledge Utility (7)
If what you learn derives largely from the culture you live in, and if individual differences derive support from variations in the home (that micro-culture of the family), it is important for people to know what learning is like in other family’s homes. The anecdote I present here reveals one case of the dynamic interplay between social relations and manipulating numbers.
Counting and punishment
In our home, the children have become skillful at manipulating numbers.Whenever they raise a problem which they might figure out, I try to take the time to work through it rather than simply give them some answer which they must accept on my authority. I look for occasions to involve numbers in what they think about. For example, when we have squabbles so serious that someone must be punished, that punishment usually takes the form of ‘go sit in that chair until you count to (some number) (in some non-simple fashion)’. The reason this developed is that, when ‘punished’, the children always wanted to know the term of their sentence. Counting provided a useful termination for the children before they could tell time. It was easy for me at first when the children had trouble counting to 40. They suffered a formal penalty but were too busy counting to feel bad. As they became more competent at calculations, giving them tasks difficult enough to generate a ‘cooling off’ period became harder.
Enjoying small jokes, I have occasionally asked them to do very difficult things, e.g. ‘count to 37 by three’s’. I do not advance this procedure as something to be imitated but rather offer it as evidence that the children found number knowledge very useful in their everyday lives.
Competition
Though I love my kids, I would not in any sense claim my family is exemplary, but it is rich in vitality and sometimes in good humor, despite the children’s rivalries which surfaces in nearly everything. My daughter Miriam, aged 5 and one half, on visiting the Logo computer lab required ofme that I write a program which would set her addition problems to do. This is not a kind of ‘computerized education’ of which I approve; but since she asked for it, I wrote her a program to quiz her on the sum of two randomly selected digits.
Robby thereupon required a program presenting some more difficult problems. So I wrote one challenging him to sum one single digit and one double digit addend. Both children were happy for a while….
Miriam mentioned at dinner, with great pride, that she could count backward from twenty by two’s. She demonstrated. When she reached zero, I asked Robby (who had been introduced to one negative number, minus 10 Farenheit, as the best temperature for keeping ice cream) what came next. He said, apparently somewhat startled himself at the realization, ‘minus two’. I congratulated Miriam on her skill. She, with irritating condescension, said that counting backwards was ‘cinchy’, and so was adding. Robby countered that adding was easy only because her program used easy numbers. Here, she dealt him a severe blow, revealing that she had been adding using HIS program at Logo. She declared that ‘cinchy’ also.
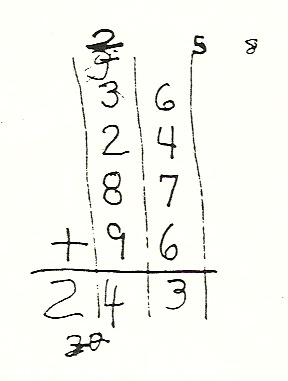
Robby had trouble mentally summing such numbers as 7 and 16 (Miriam had succeeded with comparable sums by borrowing my fingers to help her reach the answers she counted up to). The battle was joined. Robby, who had become skillful at right to left adding with carries, confidently proposed on his napkin the sum 642 plus 260. Miriam was put down, but she ignored that fact and dismissed the task. He added the numbers correctly (see Figure 1). Miriam, declaring it her turn, challenged Robby to sum 29 and 100. Because she thought it a hard problem, I infer thistask can represent the limit of her skill. Robby wrote down the answer directly then had his revenge: he set her the task of summing 66 and 78. Such is a wicked sum for beginning arithmeticians; not only are there carries, but the answer contains a third digit where each of the addends had only two digits.
Miriam was in trouble, but she charged on. “Can I borrow some fingers ?”
So we four at the table each raised our ten fingers and around she went,then again, stopping at 78. Next, restarting, she counted fingers by tensto sixty and then six more. Her procedure failed to produce a sum different from either of the numbers she was attempting to add. When I asked her about the sum, Miriam decided to back up to a more trustworthy procedure: she began writing hash marks on a paper napkin. The marks spread across the page; returning back on the same row, she made larger hash marks to discriminate them from the first pass. (I count 59 marks in that row; she may have made up the sum to be 66). Her tenacity was exemplary.
Robby’s amusement was unconstrained, as though applying such an uncontrollable technique were the craziest action he had ever witnessed.His reaction amused me, for a mere six months before he had exhibited precisely the same response to a challenge of comparable magnitude (see the earlier chapter about ADDVISOR). Although anecdotal, this is striking evidence of the amnesia about prior cognitive structures that were superseded by others.
Miriam abandoned writing hash marks for a listing of the integers in order. This second technique, though more difficult to write out, was clearly superior because one need not start at the beginning again if momentarily confused. When Miriam ran out of space on the paper, we solved the problem together. Though Robby wanted to continue, I stopped our exercise at this favorable time for all of us, and we proceeded to enjoy the rest of our now cold supper.
FIGURE 3.1
Rob’s addition of 642 plus 260 vs. Miriam’s Hash-mark Counting
THE URGE TO INSTRUCT: showing a solution (8)
Both children lay on the floor tonight hoping to induce our new Scotch terrier puppy, Scurry, to lick their ears and jump on them. Scurry is obliging and the house has been a pandemonium. Robby thus easily fell under censure for some small failing, and I told him to stand in the hall and count to 27 by fours. He griped that he could not do such an impossible task. I asserted that he could do it.
| Robby | Oh, you mean do a three at the end ? |
| Bob | No, just at the beginning |
| Robby | Oh… 3, 7, 11, 15, 19, 23, 27. |
Soon after, Miriam, for whatever reason suffering a like punishment, allowed as how she could count lots of ways, by ones, tens, fives, and twos (this is so). I told her to count by fours.
| Miriam | Daddy, I can’t. |
| Bob | To 12. |
| Miriam | That’s impossible. |
| Bob | Prove it. |
| Miriam | 4, 8, 13. |
So she had her joke on me, and in general good feeling we approached the supper table. At Miriam’s request, we listened to Beethoven’s 5th symphony as we sat down to eat. Robby told me he had finished multiplication fast in school today, that he was first in the class. I congratulated him, but, not wishing to support the competitive sense he was expressing, I decided to change the subject. I noted that I prefer the 6th symphony to the 5th. Both children then chirped up that they liked the 9th best of all. The way they responded seemed as if they were inventing a game of ‘my favorite symphony has a higher number than yours’, so I countered that I also liked the seventh, and that 6 and 7 are 13. Robby claimed that he most preferred the 9th and the 8th (I don’t believe he had heard the 8th at that time) and Miriam, “I like 3 and 5 and 7 and 9.”
In an unfair counter-move, I noted that I especially liked Opus 132 (the A minor quartet) and was properly shouted down with the complaint that an Opus was some other number, not a symphony. Miriam closed the dispute:
| Miriam | I like them all, and that’s a lot. |
| Bob | How many ? |
| Miriam | (beginning to count…) |
| Robby | 9 plus 8 is 17, plus 7 is… |
| Gretchen | 45 is the answer Rob. |
| Robby | Hey, I’m trying to think and you’re distracting me. |
Gretchen then became very insistent and showed Robby the solution to the discovery of which I was trying to lead him:
| Gretchen | How much is 9 plus 1 ? |
| Robby | 10. |
| Gretchen | How much is 8 plus 2 ? |
| Robby | 10. |
| Gretchen | How much is 7 plus 3 ? |
| Robby | 10. |
| Gretchen | How much is 6 plus 4 ? |
| Bob | (when neither had completed the procedure)…and how much is 5 ? |
| Robby | 5…Hey, wow ! The answer’s 45. |
Gretchen had no general and pervasive didactic intention, but her aggressive instruction points out how adults who have learned some clever trick insist on showing it to people who have not yet encountered it.
THE URGE TO INSTRUCT: emphasizing a problem (9)
We drive in cars a lot, and I find it hard to be patient at long stoplights. Since my children fidget whenever we wait for a red light, some months ago I introduced them to an old game:
When you encounter a red light, you chant the formula: “Red light, turn green before I count to seventeen.” — then begin counting. You win if the red light turns green before you reach the number seventeen.
This is a good game because victory is always within your grasp. One may proceed at any rate or with variations of rate he desires.
Miriam, at the age of six, counts initially at her “normal’ pace and begins slowing when she gets to twelve, drawing out both words and intervals. Rob began with the same approach; more recently, in keeping with his developing concern about playing fair at various other games, he has maintained a regular counting pace and thereby ‘lost’ the game.
As I waited at a traffic light last night, I heard Robby intone: “15, 16, 16 and 3/4, 16 and 3/4 of 3/4” and so on. The light turned green. As we moved outof the intersection, I asked Robby how many three-quarters of three-quarters he needed. He replied, “Five. But it doesn’t matter. I win every time now.” I congratulated him and noted that he had come upon one of the great puzzles of all time. Rob: “Is it a tough one ?” I told him it took over two thousand years for someone to figure out to solve Zeno’s puzzles and said we would discuss them more comfortably when I was no longer driving.
The concrete example of the racecourse paradox I gave put Achilles at the end of our driveway with an intention to go to the barn. I argued that before he reaching the barn he needs to go half-way — say to the wall of the courtyard. Robby agreed that he still had halfway to go. And, I continued, to go from there he still must go halfway — and he will have half of a half to go. And so forth. Robby squirmed a little. “But if he goes many, many halves of halves, he’ll get to where he only has an inch to go.”
I agreed, but still maintained that he had not yet reached the barn.
Gretchen added that this was called a paradox, because we all know we can just get up and walk to the barn any time we want. I continued, “If Achilles has an inch to go, he still has to go halfway, a half inch first — and that still leaves half an inch.” Robby: “And half a half is a quarter… and that still leaves a quarter to go.”
When I asked Rob if he wanted to hear the other paradox about the tortoise and the hare, he answered, “Not now…wait about six years”.
Contrasting the two exemplified forms of ‘instruction’, the most significant difference seems to be what one is trying to teach. In the first case, Gretchen tried to communicate to Robby a specific procedure that would permit him to calculate sums of uninterrupted integer sequences. In the latter case, I tried to extend Rob’s accidental engagement with a concrete problem to introduce him to a broad class of mathematically interesting problems. The former is more like ‘giving knowledge’; the latter more like ‘setting goals’.
THE OBVIOUS IS UNKNOWN (10, 11)
Multiplication has been an insistent theme for Robby. One night, about five minutes after his going to bed, as I passed through his room, Robby rose out of the covers with a groggy look on his face to ask, “Dad, is 3 times 30 90 ?” I answered his question and asked why he wanted to know; he replied,”I don’t know.” At odd moments over the intervening weeks, Robby asked is N times 10 equal to some-value. One night at dinner, the following dialogue took place:
| Robby | Mom, is 9 times 10 90 ? |
| Gretchen | Yes. How much is 10 times 9 ? |
| Robby | 9 plus 9 is 18; that’s 2. How much is 18 plus 18 ? |
| Gretchen | 36. |
| Robby | 36 plus 4 is 40. |
With this pending confusion, I cut off dialogue at this point in the hope that I would later be able to bring up the question of Robby’s understanding of commutativity in a clearer context.
Robby apparently used the tens as a discrete scale wherein each decadal increment is “the next bigger thing”. In an incident from protocol 4, (12) at age 7;3. Rob argued that when building a triangle from tinker toys, one used “the next bigger one” for the hypotenuse; consequently, when drawing a right triangle with an hypotenuse of 50 turtle steps, 40 turtle steps should serve as the equal legs because 50 was “the next bigger” thing from 40. His use of this “decadal” scale as an estimation basis can be seen in the following incident. After having asked for verification of 3 times and 7 times 11, Robby asked if 11 times 11 was 120. Responding that his answer was not perfect but nearly so, I asked how he estimated the product. He replied, “Well, I know that 11 tens would be 110, but elevens are a little bigger than tens, so the answer has to be bigger”.
During this period of multiplying by the controlled counting of decades and other number scales, the question of multiplicative commutativity was again raised at table. When Robby showed he knew that 20 times 5 is 100, Gretchen asked him, “How much is 5 times 20 ?” To this query, Robby replied: “20, 40, 60…I give up.” The following Sunday, Robby had to face the possibility of missing his favorite TV program, Victory at Sea. He complained that he might miss the battle of Midway. Gretchen countered that he would be able to see it sooner or later, that Victory at Sea had been on TV for 20 years and that the battles would roll around again.
Gretchen avoided telling him about commutativity in multiplying.
Notice that this ‘obvious’ property, which adults freely use in mental calculation, was something that Robby had yet to discover. In this case, the child’s ignorance was of little long term consequence. But there do exist documented cases where such ignorance of the obvious must severely constrain any understanding we ascribe to a child. For example,Miriam’s understanding of strategic play in tictactoe did not recognize the importance of opening advantage. (13) In both of these cases, an important aspect of the child’s representations is that they must function tolerably well, even though quite partial in the specific sense of omitting significant elements of the mature representation.
CONCRETE ACTION IN A NON-SQUARE WORLD (14)
Two of Robby’s current interests have come together in a productive way. Following my buying him a new tool box, he elected to take up wood working in an after school program. His delight in building ship models led him to declare he was going to build a 9 foot long wooden aircraft carrier. I voiced absolute objection but, content to let the fantasy grow, said he could plan the ship and scale down the model later to some reasonable size. Later he asked advice:
| Robby | How much is 20 times 52 ? |
| Gretchen | 1040 [Gretchen computes accurately and quickly]. |
| Robby | How much is 52 times 20 ? |
| Gretchen | 1040. |
| Robby | [Looking puzzled] It’s the same thing…How much is 20 times 52? |
| Gretchen | 1040. |
| Robby | Dad, how much is 9 feet take away four ? |
| Bob | 5 feet. |
| Robby | No, I mean take away 4 inches. |
| Bob | Come here and I’ll show you. |
Robby came to my desk and worked out this excercise:
9' --> 8' 12"
-4" --> -0' 4"
---- --------
?? --> 8' 8"
This dimension, 8′ 8″, is for the sub-structure of the carrier. The 9′ flight deck will overhang 2 inches at each end.
In response to this and other expressions of the need to draw plans, I
introduced Robby to orthographic projection (front, side, and top views).
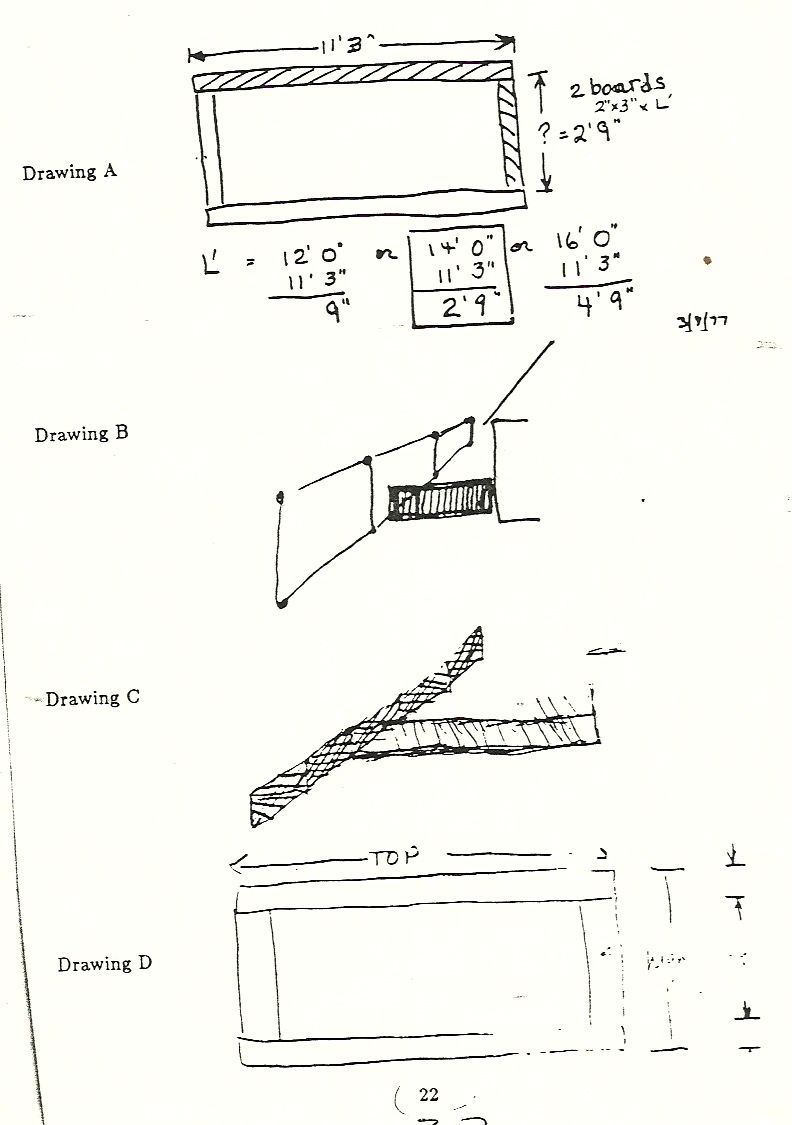
Thus when last week I entrained him in my task of building a run for our dog (of 2 x 3’s and hardware cloth), it seemed appropriate to ask him to draw plans. This was even more the case because I had formerly asked Robby to compute dimensions on the sizing drawing to determine how long should be the 2 by 3’s we needed to make the frame. We were to enclose the two ends of an area 11′ 3″ wide. Because I knew the available lengths of 2 X 3’s are 12′, 14′, and 16′, I set up the three sums underneath the drawing and had Robby compute the board residues we would have after cutting out our lengths. We selected the 14′ length as what we wanted because each board would would yield a length and an end piece (we did not expect to need a 5′ high fence for our Scotch terrier).
In the process of explaining that sizing drawing and my objective for the project to Robby, I drew on the reverse of the 3 x 5 card with drawing A, the drawing B (see Figure 2). The purpose was to locate our additional fence in a picture Robby would recognize (the fence behind the back of the house we lived in). As I gathered my tools and set up saw horses for working on, Robby drew his ‘plan’, drawing C. Contrasting drawing C with drawing B, you will notice it has vertical lacing similar to my earlier drawing (the hardware cloth, with its square mesh, was rolled up beside where Robby was sat drawing his plan), and his drawing is more detailed in showing the diagonal mesh of the chain link fence. Robby’s drawing placed our planned construct in its setting, its context, but was useless for keeping track of the various dimensions one might want to use in calculations. I showed Robby, in drawing D, the kind of plan I had in mind and tried to indicate its purpose. I was surprised that his new idea of a planning drawing leaned so to verisimilitude.
FIGURE 3.2
Since Robby did not seem interested in my abstract drawing, we proceeded to the morning’s rough carpentry. If you can’t compute precisely the sizes of the parts you need, you can fall back on the handy-man’s technique of transferring dimensions, i.e. you lay a board next to the place it is to go and mark off the size it need be to fit. We proceeded in this simple, traditional way.
Transferring dimensions is frequently the procedure of choice in the repertoire of both the craftsman and the handy-man; one reason is that the rustic carpenter is thus less vulnerable to the failings of his calculation skills; a second is that few things in this world, either natural or manufactured, are square; a third reason, decidedly relevant in this case of force fitting a wooden frame between a chain link fence and a masonry wall, is that you must sometimes worry about how your new manufacture relates to other things it is used with. Thus one lesson Robby could find in this project is that if you can’t make an abstract plan, the concrete constraints may be enough, may even be your best bet, to finish the work at hand. Similarly in calculations, if you don’t remember or can’t understand some perfect algorithm, your commonsense knowledge helps you muddle through and may even be adequate to your needs. Though on the surface this may seem a negative lesson, it may be among the most important notions he can come to appreciate. Indeed, if particular solutions to problems are messy and inelegant, general solutions to really hard problems are usually impossible. As the following characterization of his learning shows, such a conclusion is quite congenial to Robby’s own problem solving practice.
THE CHARACTER OF NATURAL LEARNING
FLEXIBLE KNOWLEDGE: extending a known solution (15)
At a parent-teachers meeting in the school both my children attend, the teachers were demonstrating the kinds of activities the children perform to develop their math skills. I managed to embroil myself in a minor conflict with a third grade teacher.
The woman had demonstrated to me the use of Dienes blocks as a concrete representation for children of the problems one encounters in addition (I think that is fine). I asked her if the children, using this medium, ever added from the higher order of columns of blocks to the lower. She noted both that they did and that she always instructed them to add ‘from right to left’. “Why?” Because, she explained even though they can add from left to right with Dienes blocks, they have to add from the right when they use paper.
Since she doubted that one could add left to right in the standard vertical form of addition, I exemplified the two-step procedure described in ADDVISOR. The teacher’s counter-argument is shown by the sum she posed to me: 36 + 24 + 87 + 96; she claimed that one could not add it the same way. She noted that third grade children get to do such difficult sums by the end of the year. When I performed the sum in the same fashion, she argued that the procedure was too inefficient for computation. I let the matter lie, even though I believe a short procedure of mysterious steps is not so good as a long procedure of well understood steps.
The previous background material helps explain the particular puzzle I posed to Robby. I asked him to perform the sum over the four addends. Please note that I had never posed such a problem before and was unaware of his encountering any such (the most similar components he had confronted were cases where he had to add a carry with two other addends in a column). I explained to Rob that one of the teachers at the parent-teachers meeting (one he had never met) had showed me this problem as one she thought would be hard. I asked Robby to try it so he could develop an opinion on the claim.
Since Robby, after his experiences with ADDVISOR, had come to prefer adding right to left with carries, his exercise did not address directly the issue the teacher and I had discussed, but it did address how readily he could generalize the procedure he had learned for this new situation. As will be seen, it also shows what sorts of number sense are useful guides in that process. I wrote the addends on a 3×5 card in vertical format with column division lines. Robby took the card and sat on a couch across the room.
Whenever he asked for help, I answered Robby’s questions. He asked three times for verification of intermediate results. His first was “Is 8 + 9 equal to 18 ?” (16) When told that the sum was seventeen, he asked if 17 plus 5 equals 22.The third query: “Does 6 + 7 equal 13 ?” The order of the questions implies he was working on the sum from left to right. Next, Robby volunteered that 22 plus 23 equals 45 but that 45 could not be the sum because one of the addends (‘the other numbers’) is 96. He then asked a series of other questions about adding “this and this and that and this”. I told him I couldn’t see what he was referring to and that, if he wanted help, he should bring the work to me. He replied, “No. I’m not finished.” After a pause, “243 ?”, as he brought the work to show me.
FIGURE 3 Robby’s Scratch Addition
I asked Rob directly if he had ever done any other problems such as this, and he said no. When I asked how he knew to treat the 2 of 23 like a carry, since he had never done it before, he said “You don’t have room for it here (in the unit’s column); if you put it over there (in the ten’s column), your answer would be double big.” I take his response to mean that if the 2 were pushed into the ten’s column, the ten’s digits would be forced into the hundreds column; the answer would be ‘double big’ in the sense of having too many digits in the answer.
This little experiment produced a happy result. Such a constructive use of analogy is highly desirable and often effective. The child is in control; the personal extension of ideas he comprehends leads to the creation of more authentic knowledge. In this case, the minimal extension required to solve the problem may obscure the process involved. Next we turn to an example of calculation where analogy is used to bridge a wider gap.
MULTIPLICATION AND MONEY (17)
The term ‘commutativity’ as used in the following refers to only the most trivial sense — as a good trick that adults generally know can be applied to choose between two ways of performing a calculation. I try to ‘tell’ Rob that the reversibility of terms in sums, which he recognized, has its counterpart in multiplication. What Robby reveals of his methods of problem solving is more interesting than the prosecution of my agenda in the dialogue.
| Bob | With adding it doesn’t matter which way you do it. |
| Robby | Right. |
| Bob | What about with multiplying? |
| Robby | It doesn’t matter. |
| Bob | Well, then, if we had a real hard multiplication like 25 times 4…. |
| Robby | That’s 100 |
| Bob | How’d you figure that out? |
| Robby | ‘Cause four quarters are a hundred. |
| Bob | What you did, Robby, was to turn these around, and you said, “We’ve got 4 times 25.” That’s a hundred because multiplication has the same property. |
| Robby | As money, sometimes…. Because four quarters of money is, uh. It goes like this: 25, 50, 75, 100. |
| Bob | You’re right. Well, the point I’m getting at is that this commutative property, not mattering which way you do it, is true also of multiplication. Do you understand the property, Rob ? |
| Robby | Yeah. |
| Bob | And that same property is true of multiplying? |
| Robby | Yes. |
| Bob | But is it true of subtraction? |
| Robby | No. |
| Bob | O.K. Thank you for working on this with me, Robby. |
Two points deserve comment. First is the usefulness of capturing the agenda of the experimenter with mechanical recording in order to account for its impact on the subject. In this case, my focus on my agenda and lack of sensitivity to his behavior permits the argument that his deformation of a ‘number’ problem to a representation rooted in money-based experiences stands clear of my activity as an example of common-sense problem solving.
The second point is the particularity of the computations Robby uses, as in his mapping of the twenty-five 4’s multiplication onto his money-counting algorithm. While I remark that “multiplication has this same property” referring to commutativity as in addition, Robby’s understanding is that multiplication has the same property ‘as money’. This example suggests that howevermuch Robby’s calculation abilities may appear as standard on the surface, his actual computations are a collection of clever tricks based upon his empirical understanding of number’s application is a variety of domains. Common-sense problem solving could be much less a matter of inference than of trying to apply a variety of points of view — then following whichever one seems to work best. Abduction dominates induction. An important component of natural learning must be discovering in novel situations which components of already existing knowledge are useful, coupled with the construction of a solution based on this analogy. But if analogy is a central process in problem solving and learning, such processes must often go wrong. We now turn to examples of such natural confusions.
NATURAL CONFUSIONS: place value and scale conversions (18)
The children had been exclaiming how they couldn’t wait for Christmas.
“Tomorrow is Hanukkah. Maybe we should get one present for Hanukkah and all the rest for Christmas.” Believing this a strategem more than an upsurge of ecumenical spirit, I objected that we had no place for presents, had not even got a Christmas tree yet. Dragging my foot when they declared we should get one right away, I asked where could one go in this small apartment, what size should it be.
My reluctance was partly nostalgia. While the children ran about finding a yardstick, then a six foot folding rule for measuring the least cluttered corner of our quarters, I regretted those impediments preventing me from returning home to harvest one of the hundreds of trees my wife and I planted years ago. Our trudging out in the near-Christmas snows to select, cut, and carry home our own holiday trees was a small but significant lost joy. The children quickly brought me back from this reverie.
Miriam ran to get a high stool while Robby stood with the six foot rule against the wall and butted to the floor. Miriam proposed to measure from the top of the rule to the ceiling by climbing on the stool and using the yardstick. To prevent her from such an attempt, I suggested to Robby that he push the top of the rule to the ceiling and let Miriam measure to the floor from its lower end. Thus we arrived at our two measurements: 72 inches (read from the rule); and 24 inches (read off the yardstick).
Robby has been studying measuring at school, so he knew that we should be able to specify our maximum tree size in feet and inches. Miriam decided to leave this problem to Robby, who offered to work it out on my chalkboard. Writing down 72 and 24 in columnar format, Rob proceeded directly to the sum 96, which he noted was 96 inches. “Now we have to do the feet.” I suggested we could figure out the feet an easy way. “How many feet is 24 inches ?” After a pause, Robby said “Two.” and wrote down ” 2′ ” on the chalkboard. “How long is my rule ?” “Six feet”, Rob replied; he wrote a 6 under the 2 and proceeded to the sum. Then he continued: “We’ve done the feet. Now we have to do the inches”. Thus, adding in the 2 and 4 inches (from 72 and 24), he declared we should not get a tree bigger than 8 feet 6 inches.
When I asked if he were sure his conclusion was correct, Rob informed me,”Dad, I’ve had six weeks of measuring. I’ve done this a lot.” When I asked more specifically had he done THIS in school for six weeks, Robby responded, “Well, I didn’t count, but it was something like six weeks.” I continued to probe his calculation:
| Bob | Rob, how come you added the 2 and 4 to get six inches? |
| Robby | The tens are the feet part. [writing ‘FEET’ on the chalkboard over the ten’s column.] |
| Bob | If the tens are the feet part, why don’t 7 and 2 make 9 feet? |
| Robby | [After a pause] Then it would have to be 10 inches to the foot but that it’s really 12 inches to the foot. |
| Bob | Well, if 12 inches is one foot and 24 inches is two feet, how much is two feet take away 24 inches? |
| Robby | Zero. Oh…you mean we used up the 4 in the 24 inches for the two feet? |
When I agreed, Robby returned to the chalkboard, erased the 6 of 96 in his sum, and replaced it with a 2. Then, changing his mind, he complained:
| Robby | Dad, you confused me. [Restoring the sum to 96 inches.] The tree has to be less than 8 feet 2 inches. |
| Bob | Where’d you get the 2 inches? |
| Robby | There, from the 72. |
| Bob | No. That’s not correct. |
| Robby | It isn’t?… I think we used up the 2 in the six feet, because it’s 2, 4, 6, 8. Eight feet and zero inches! |
| Bob | How do you know you used up the 2 inches? |
| Robby | Feet are not tens, they are twelves. |
We then, for verification, took out my folding rule and counted twelve inches for each foot. Robby kept track of the feet on his fingers and reached an even 6 feet as we came to the end of the rule.
As I jotted notes in my journal, Robby climbed into the chair with me and asked me to explain what I had written. So I did. He claimed that he never believed some of the things he had said, specifically that the 2 came from the 72. When I asked if it was OK to make mistakes, he said “Yes” and laughed.
USING MULTIPLE REPRESENTATIONS (19)
After the specific confusion of feet and tens Robby had shown, I bought him his own six-foot folding rule, one with foot markings every twelve inches. Further, I decided to tackle his confusion directly by contrasting the addition of 76 and 29 with the addition of 7’6″ and 2’9″. We worked at my desk, which has a small chalkboard nearby. Even though we had the concrete support of various folding rules and a yardstick, Rob remained unable to develop any stable understanding of the relations and contrasts between these two number scales. Reviewing the transcript, I could accept the blame for this and admit that I tried to push too hard in asking him to add numbers expressed in yards as well as feet and inches. But the more important point coming from this didactic failure is that the ideas were not yet fully familiar, they were not yet fundamentally his own in some profound sense. Thus he could not use them to understand more novel problems.
NATURAL CONFUSIONS: the multi-add algorithm (20)
When one day Rob stayed home from school with a headache, he recovered enough with some aspirin and a long nap that in mid-morning he entered the study and asked me to join him at a frisbee game. I countered that inasmuch as he was missing school, I wanted him to do something ‘academic’; I suggested he read the next chapter in Jane Goodall’s book The Wild Chimpanzees. With that accomplished, somehow we fell into talking about multiplying. I told Robby if he had a good algorithm, one could multiply even very large numbers. Disbelieving that claim, and believing he knew how to multiply, Robby first set out a big number for me to multiply — then chose to tackle it himself. He used an algorithm of his own invention in which he multiplied digits within columns and carried tens digits from columnar products as one would in addition; I call this the “multi-add” algorithm (21).
| Bob | 13 thousand, zero, three, zero, and you’re going to multiply that by 13 thousand, 3 hundred and thirty…. O.K. Now draw a line under that [See product 1 in Figure 4]. What do you do now? |
| Robby | I do zero, nine, oh, nine, 2 [writing in the ‘product’, term by term, right to left, in product 2]. |
| Bob | Zero times zero is zero. 3 times 3 is 9, 3 times zero is zero, 3 times 3 is nine, and 1 times 1 is 2? ‘Cause that’s what you wrote down, right ?… What you’re doing is putting a line down here, right ? [as I draw lines between columns] |
| Robby | Yeah. |
| Bob | And you’re multiplying every term. You’re saying 0 times 0 is 0. 3 times 3 is 9. 3 times 0 is zero. 3 threes is 9 and 1 times 1 is 2. O.K. Two things you can say about that. First: how much is 1 times 1? |
| Robby | 2. |
| Bob | No. That’s 1 plus 1. O.K.? |
| Robby | Oh ho. 1 times 1 is 1 |
| Bob | O.K. So that’s now correcter, right? Within the multiplication you did there, you did it fine. |
FIGURE 4 Rob’s First & Second Multi-add Problems
Rob corrected the leading 2 of his product to a one. After I explained that I really didn’t understand what he was doing, he erased the completed problem and began another.
| Bob | Let me take a look at that. Holy smokes. 381 thousand, 156. Now do you want to multiply the same way on this problem as you did on the last one? |
| Robby | Yeah. Can I do it here? |
| Robby | This 6 twos — must be 12. |
| Bob | O.K. |
| Robby | Carry the 1. |
| Bob | [Probing] Why don’t we just go ahead and do it column by column? Then worry about the carries after ? |
| Robby | Daddy [exasperated]. |
| Bob | Yeah. |
| Robby | Daddy [writing a 2 and carrying a 1]. 6 [the sum of the digit 5 and the carry 1] times 4 — |
| Bob | So you carry 1 and get 6 fours. |
| Robby | Yeah. |
| Bob | How much is that? |
| Robby | 6 fours…. 12. |
| Bob | 6 fours are 12? |
| Robby | No…. 18? |
| Bob | That’s 6 threes. |
| Robby | [mumble] 22. |
| Bob | You said 22, but that’s not correct. 6 fours are 24. |
| Robby | [writing] |
| Bob | So you put down the 4 and are carrying the 2? Hold on. Slow down, young fellow. You’ve got one and you’re adding, you’re carrying a 1. |
| Robby | Yeah. I should have carried the 2. |
| Bob | Let’s take it slow and easy. Back up. So you’ll cross that out [the 1] and carry the 2. What have you got now? |
| Robby | [writing] 3 [1 plus 2 carried] times 3 is 9. |
| Bob | O.K. |
| Robby | 1 times 3 is 3. |
| Bob | Three. |
| Robby | [a groan for trouble encountered] |
| Bob | That’s a good one, isn’t it. |
| Robby | 8 times 9 is…8 nines…. |
| Bob | Is that too tough? |
| Robby | Yeah. |
| Bob | Try 10 nines and take away 2 nines. |
| Robby | 10 nines. What’s that? 91? |
| Bob | 10 nines is what? |
| Robby | 91? |
| Bob | No. |
| Robby | What…. 90? |
| Bob | If it’s 9 tens, it’s 90. Take away 2 nines, which is 18. |
| Robby | 18. |
| Bob | So it’s 90 take away 18. |
| Robby | 62? |
| Bob | That’s close. It’s 72. |
| Robby | Aggh. |
| Bob | So you put down the 2 and carry the 7 ? [describing Robby’s action, not directing it] |
| Robby | 7 and 3 is 10. 10 threes. |
| Bob | Are what?… Zero, thirty. So you put down the zero and carry the three…. What you’ve done is to invent a new kind of way of doing this. What you’re doing is very interesting but it’s not multiplication the way other people do it. |
| Robby | I do it this way…. It’s easier. |
| Bob | I’m sure it is, though I don’t know that it’s so very easy. |
As our problem solving continued, I tried to explain to Rob why his algorithm, even if he should perform it correctly, would be different from what other people meant by multiplication. The attempt met with no good success. His own experience convinced him that multiplication is like addition — didn’t he multiply two numbers by repetitively adding the first the number of times represented by the second ? Given that opinion, should not the addition algorithm for large sums be modifiable for large multiplications ?
The analogical extension Rob imagined was primarily a syntactic modification based on a correct, semantic comprehension of the relation of the parts. If commitment to his understanding was a weakness in this case, the weakness was very strong. I conclude that he needed a different sort of experience, one where the elements and their relations could become as familiar to him as were those of addition but through which he would be able to see that a multiplication algorithm must be quite different from his addition algorithm. That is, he needed some alternative model from which by a constructive use of analogy he could create for himself the standard multiplication algorithm.
INSTRUCTION AS INVENTION: MEMORIZATION AND ENGAGING GAMES (22)
For some time, Robby has been asking me for help in memorizing single-digit sums. Whenever I have to memorize relations which demand an unthinking but accurate response on my part, I use flash cards and drill to embed the process in my mind. I don’t want to emphasize this method with Robby now because I want to avoid his developing the idea that this is what ‘learning’ is. These values confronted me with a problem: how can I engage the children in an activity wherein addition of single-digit sums is an integral element and wherein the demand for that addition is repeated in rapid cycles.
One game I know with these attributes is “shooting craps”. This is a gambling game played with two dice. The players put money in a pot, and one person rolls the dice. Should he roll a sum of 7 or 11, he wins the money in the pot. Should he roll some other sum, that becomes his ‘number,’ which he attemps to match in subsequent tosses. In these succeeding tosses, should he roll a 7 or 11 before he matches his number he loses and the turn passes to another of the shooters. After introducing the children to the game, I found they were fascinated (they have played consistently for several days), and they even introduced the game to visiting friends.
The only drawback I’ve found in the game (aside from its centuries old ill-repute as the pastime of gamblers and ne’er-do-wells) is its limited range of sums, i.e. with six faces on each cube and both numbered 1 through 6 inclusive, the highest sum is twelve. Robby has mastered those sums adequately but requested help with sums such as 6 + 9 and 7 + 8. The regular pentagon generates a regular solid of 12 faces, and two of these could yield sums to 24. (But such would be hard to make, would roll too well, and would provide a less sharp definition of the dot patterns than does the cube.) I preferred the simpler alternative of modifying the patterns on a set of standard dice. I now have two dice with these patterns of dots (4 through 9 dots):
. . . . . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . . . . .
4 5 6 7 8 9
The possible ranges of sums from mixing standard and super-dice are 2 through 12 (two standard dice), 5 through 15 (one standard die and one superdie), and 8 through 18 (two superdice).
The children have been playing ‘super-craps’ today. From the playroom I hear Robby lament “Oh no, seventeen” (with a different range of sums we picked 13 and 17 as numbers analagous to 7 and 11) and from Miriam, “15’s my number”. Using the higher range of dice has slowed their game marginally but has not made it unattractive.
A final concern for such a technique of helping children learn single digit sums: what sorts of representations are involved in their addition processes in this task? What I see is the children translating the problem into their standard addition procedures. That is, Miriam starts at the larger number and counts up to the sum. Robby apparently estimates and refines, e.g., “9 + 6 is 16, 15”. This I take to be counting back from a sum, of the smaller digit and the larger rounded to 10, by the difference of that larger digit and 10.
A week after the introduction of my children to ‘super-craps’ their mother and I met Robby’s teacher for the first of periodic conferences. We discussed the problems he had with other children in the class (those typical for a new boy moving into the neighborhood). The teacher volunteered that she had been worried about Robby’s inadequate command of “number facts” until the last test, wherein he responded accurately and rapidly to single digit addition problems. The test was given five days after the children had been introduced to shooting craps.
A subsequent variation on the use of the dice was in subtraction problems. The green superdie pattern ranged from four to nine. I made a mixed set of one green die and one standard red die. The problem posed was to take away the count of dots on the red die from the dots on the green superdie. Since the problem was not implicated in any game, it was engaging only for the challenge it offered. Robby has played with the dice occasionally and performed the subtractions. Once in a while, the subtractions produced a result less than zero (for example, a red 6 and a green 4 resolve to minus 2). When he expressed those negative differences as ‘zero minus 1’ and ‘zero minus 2’, I asked Robby if that was the way they discussed such numbers at school. He replied that they hadn’t talked about such numbers at school yet.
Comparing this game with the earlier computer experiences of ZOOM and ADDVISOR, I judge playing with the superdice as more like using ZOOM than ADDVISOR. ZOOM provided a bounded world where drawing experiences required developing familiarity with a numeric scale for eventual satisfaction of the child’s objectives. ADDVISOR has a different quality, that of an articulate explication of a representation, one highlighting the linear independence of columnar sums and their permitted interactions. Its limitations derived from the sharp focus on a particular representation, which was also the basis of its usefulness. We turn now to another program with the same character.
GUIDING CONSTRUCTIVE ANALOGY (23)
For the past six weeks or so, Robby has been asking me to help him learn
multiplication. He needed a richer conception than “it’s the same as adding the number so many times.” When I asked him why he wanted to learn to multiply, Robby explained that he didn’t want to have to learn it in school; pushed further, he noted some multiplication problems were within the next few pages of his math book. The first question is one of representation. What is the prototypical problem in which multiplication is used? It is most usefully exemplified as the process by which one can find out how big is some rectangular area. Such a description is coherent with the uses of the Cuisenaire rods and the Dienes blocks Robby has available in school.
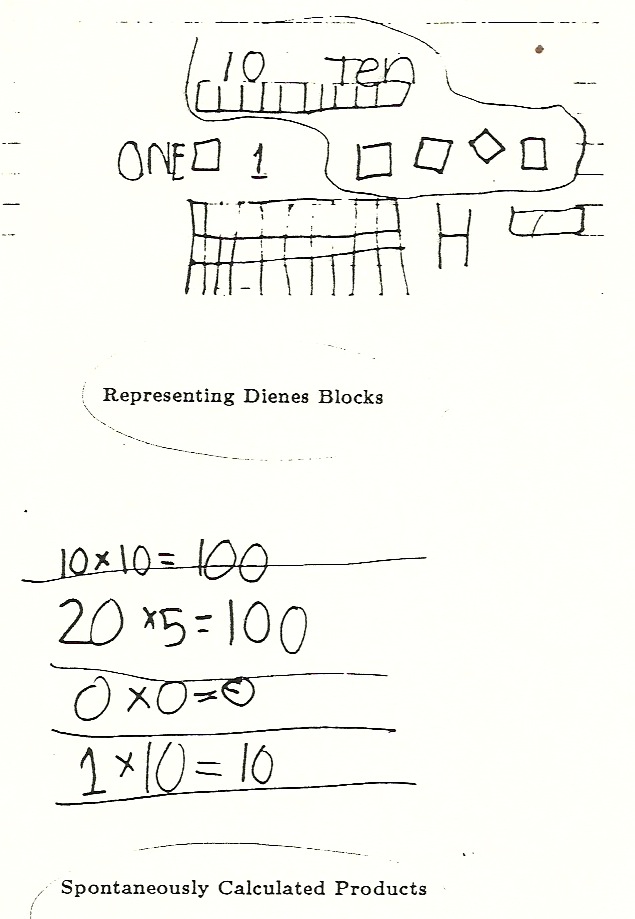
FIGURE 5
Representing Dienes Blocks & Spontaneously Calculated Products
Robby’s explanation of what Dienes blocks are and of what numbers he can multiply are shown in the first two items of Figure 5. When asked if he had been taught these specific products in school, he said, counting on his fingers,”It’s 10, 20,…, 100; and it’s 20, 40, 60, 80, 100!” Beyond this compatibility, I saw Robby’s familiarity with the ‘flat’ (the 10 x 10 square of the Dienes block set) as a means of helping him develop first, an estimate of how big a product is and second, a tool for computing how big a product is.
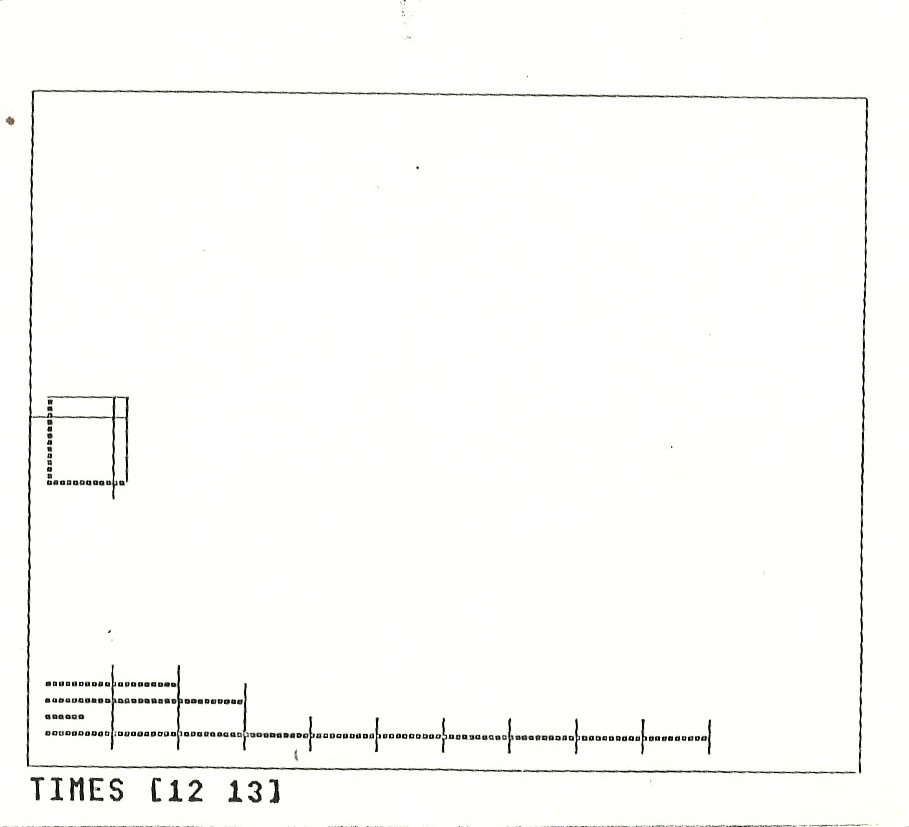
As a consequence of Robby’s interest, I wrote a program for the Logo computers to help him understand what multiplication is. The intention of this program is that it be a tool, not so much for computation as for flexibly representing a computation. The program is invoked by typing its name and two numbers, e.g. TIMES [12 13]. The resulting pictures of its execution are shown in Figure 6. TIMES displays its multiplicands as two perpendicular rows of tiny squares. The product is represented by extending parallels to each row of squares to complete a rectangle. Next, at the child’s direction, the program breaks up the rectangle into a grid of 10 x 10 squares and ‘left overs’ to help the child estimate the product (24). A first order estimate of the product is made by summing the 10 x 10 squares. The product can be computed by adding together the four single digit products. That is, for AB x CD, in Figure 6, the product is: (A x C x 100) + (B x D) + (A x D x 10) + (B x C x 10). In a final step, TIMES displays these four partial products at the bottom of the display in rows, each of which may contain as many as one hundred unit blocks.
FIGURE 6 TIMES 12 13
When Robby first encountered TIMES, my purpose was to see if this sort of tool could help him grasp a representation which would greatly expand his conceptual range. I have come to suspect, since my work with ADDVISOR, that such an achievement is inspired by an immediate exposure of the child to the power of the ideas involved. Let me be more concrete. We usually teach children to multiply numbers such as 2 x 3 and 6 x 2 because
18 x 21, as computed by the standard algorithm, is difficult to keep track of and impossible to explain. Thus, in:
18
x 21
------
18
36
------
378
How does one explain that there are two (and only two) intermediate
products and that the lower one is shifted one place to the left? Numbers of this magnitude, however, are such as Robby freely choose to trying multiplying.
| Bob | What numbers for TIMES ? |
| Robby | 20 times 20. |
| Bob | This program tries to show that a good way to think about multiplying is like trying to figure out how big rectangles are…. You can think of one number you multiply with as being one side and the other number as being the other side. And the product, the product is like how big the whole area is in here. That’s what multiplication is mostly used for, to do things like that. Does that make any sense? |
Robby responded with sullen looks and said he was reluctant to use the program. He did agree, however, to use it one time. After I invoked TIMES with the numbers 20 and 20:
| Program | [Displays the question, “How big is the product?”] |
| Robby | Do I have to answer that question ? |
| Bob | Can you make a guess ?… You don’t want to guess? |
| Robby | No. |
| Bob | Don’t. The next thing, when you press the space bar — |
| Robby | [presses the space bar twice] |
| Program | [Displays the product as a rectangular array. See Figure 6] |
| Bob | This is to help us guess. It makes big blocks that are part of the answer. |
| Robby | Oh. 400 could fit in there [smiling] |
| Program | [Continues on to display the product in stacks of length 100.] |
| Bob | Right. That’s the answer. Each of those blocks, like a hundred, will fit in there. |
| Robby | Oh. The ans — 20 times 20 is 400! |
| Bob | Yeah. You can see 400 will fit in there ’cause each one of these [gesturing towards screen] is like one of the flats of the Dienes blocks. And this, at the bottom, is just another way of lining up 400 things — with a hundred in each layer of the pile…. Want to try another one? |
| Robby | [smiling] O.K….. [keying TIMES 18 21]. |
| Bob | 18 by 21. Wow! That’s going to be a tough one. |
Robby continued working on this problem. He appeared to use the rectangular array of blocks to develop an estimate of what the product should be then use the linearly stacked blocks as a basis for calculating the product. For example, in Figure 7, 18 times 21 can be calculated as 200 plus 160 plus 10 and 8.
This program focused on providing a child with a representation for a problem which could be meaningful in terms of his past experience and could be useful in the sense of bringing within his grasp problems otherwise beyond his reach. Like ADDVISOR, TIMES is focused on the articulate explication of a representation through its use in solving particular problems. What such programs gain in specificity — as contrasted with ZOOM, for example — they lose in flexibility.
CONCLUDING COMMENTS
If we ask what we can gain as scientists from this exploration of a child’s natural learning, I believe we can come away with a sharpened perception of how difficult it may be to answer the core developmental question, ‘What are the precursors of the mature forms of common-sense knowledge?’ In addition, I am convinced that it is essential to capture the richness and centrality to learning of the social milieu. Concerning education research, attention to powerful problem solving ideas, such as the assumption of linearity, and to multiple representations and their interactions will be valuable. Moreover, we can now try to instruct by inventing new little worlds of experience which relate directly to the particular experiences of individual children. This use of computers as a flexible medium for creating learner-specific, crisply-articulated experiences is likely to be the most important contribution of information technology to education — if instructors become masters of the programming languages they will need to use.
With respect to methods for further study, the clearest need is to go beyond anecdote. This argues the profit of more extensive data collection, even of going so far as to capture a complete record of a subject’s behavior and learning for specific domains for an extended period of time. Even though the instructor may be an engaged experimenter, mechanical recording of his behavior can help the analysis to account for the effect of his behavior on the subject of the study.
Such a study has been undertaken, in fact. In the period following the collection of these protocol materials, I completed an extensive and intensive study of the learning of my two older children. One report of that work is the analysis of my daughter’s learning in Computer Experience and Cognitive Development. The concluding study of this collection, Extending a Powerful Idea, represents a developed analysis of a part of Robby’s activities during the same period of time.
Footnotes:
(1) H. Simon, 1969. See Chapter 2.
(2) See their fundamental work Human Problem Solving, 1972, and more recent descriptions by Newell of production systems and their evolution, as in his invited address to the 1985 Cognitive Science Society Conference.
(3) Barker and Wright, 1955,
4) This observational material was collected in 1976 and 1977.
(5) From Protocol 10, at the age of 7 years, 3 months (7;3)
(6) Minus two and minus ten. See the next sketch from protocol 6, which preceded this incident by a few days, and from protocol 9 under the heading “Instruction as Invention”
(7) From Protocol 6, at age 7;3;1.
(8) From Protocol 15, at 7;6.
(9) From Protocol 20, at 7;9;13.
(10) From Protocol 14, near 7;4;
(11) see also the related Protocol 13 under the heading “Guiding Constructive Analogy”.
(12) Previously reported in Chapter 1 of Lawler, 1985. Now at LC1bA5 The Development of Objectives.
(13) See pp. 131 ff. in Lawler, 1985.
(14) From Protocol 16, at age 7;7
(15) From Protocol 7, age 7;3
(16) I believe this tentative sum is shown in Figure 3 at the upper edge of the card to the right of the unit’s column, as is a ‘5’, which I take to be the intermediate sum of ‘2 + 3’ from the ten’s column.
(17) From Protocol 17, at age 7;7
(18) From Protocol 11, at 7;4.
(19) From Protocol 12, at 7;4,(a few days after protocol 11)
(20) From Protocol 21, at age 7;9.
(21) Miriam invented a similar algorithm years later, as reported in Chapter 7 of Lawler, 1985. Now at LC2bA7 The Genesis of Microoviews.
(22) From Protocol 9, at age 7;3.
(23) From Protocol 13, at 7;4.
(24) This representation was suggested to me by Greg Gargarian.
REFERENCES
Barker, R. and Wright, H. Midwest and Its Children. Hamden, Ct: Archon Books, 1971 (original edition 1955).
Fang, J. Towards a Philosophy of Modern Mathematics. Hauppauge, New York: Paideia series in modern mathematics, vol.1, 1970.
Feynman, Richard “New Textbooks for the ‘New’ Mathematics.” In Engineering and Science, March 1965. Pasadena: California Institute of Technology. Also see his further comments in the autobiography, Surely You’re Joking, Mr. Feynman. New York: W.W. Norton, 1985.
Goodall, J. In the Shadow of Man. Boston, Houghton Mifflin Co., 1971.
Inhelder, B, and Piaget, J. “Flexibility and the Operations Mediating the Separation of Variables,” a chapter in The Growth of Logical Thinking from Childhood to Adolescence, translated by A. Parsons and S. Milgram. New York: Basic Books, Inc., 1958.
Langer, S. Philosophy in a New Key. New York, N.Y.: Mentor Books, The New American Library, 1948.
Langer, S. Mind: An Essay on Feeling, Volume 1. Baltimore, Md: The Johns Hopkins Press, 1967. See especially chapter 5, “The Idols of the Laboratory”.
Lawler, R. One Child’s Learning. Unpublished MIT Doctoral Dissertation, 1979.
Lawler, R. “Logo Ideas”, a column appearing in Creative Computing in 1981-82.
Lawler, R. “Designing Computer Based Microworlds” In M. Yazdani (ed.) New Horizons in Educational Computing, Chichester, England: Ellis Horwood, 1983. Distributed by John Wiley, Inc.
Lawler, R. Computer Experience and Cognitive Development. Chichester, England: Ellis Horwood, 1985. Distributed by John Wiley Inc.
Levi-Strauss, C. The Savage Mind. Chicago: University of Chicago Press, 1966.
Minsky, Marvin “Form and Content in Computer Science.” ACM Turing Lecture, August 1969; published in the Journal of the Association of Computing Machinery, April 1969. Also available as Memo No. 187 from the MIT Artificial Intelligence Laboratory.
Newell, A. and Simon, H. Human Problem Solving. Englewood Cliffs, N.J.: Prentice-Hall, 1972.
Papert, Seymour (1971A). “Teaching Children to be Mathematicians versus Teaching About Mathematics.” In International Journal of Mathematical Education in Science and Technology. New York: John Wiley, 1972. Papert’s papers are available from the MIT Arts and Media Technology Center.
Papert, Seymour (1971B). “Teaching Children Thinking.” In Mathematics Teaching. Leicester, U.K.: The Association of Teachers of Mathematics, 1972.
Papert, Seymour (1973). “Uses of Technology to Enhance Education.”
Papert, S. Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books, 1980.
Piaget, Jean “How Children Form Mathematical Concepts.” Scientific American, November 1953; reprint 420. San Francisco: W. H. Freeman and Company.
Piaget, J. Biology and Knowledge. Chicago: University of Chicago Press, 1971.
Piaget, J. and Inhelder, B. “The Development of Operations of Combination,” a chapter in The Origin of the Idea of Chance in Children. New York: W.W. Norton and Co., 1975.
Simon, H. The Sciences of the Artificial. Cambridge, Mass: MIT Press, 1969.
Formulation: FOR THE WORLD OF EDUCATION
The best progress in education will come not from the instruction of the ignorant BUT rather through sensitization of teachers to the profound and hard aspects of everyday representations so that they can recognize opportunities to highlight them when they recur as problems for kids in everyday experience.
It may be much easier to program machines to do this than to reprogram the teachers of today.