LC1bA4 ^
Extending a Powerful Idea
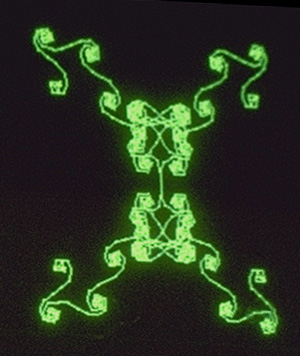
Symmetrical 17-node Inspi Design
The Argument
Mathematics is much more than the manipulation of numbers. At its best, it involves simple, clear examples of thought so apt to the world we live in that those examples provide guidance for our thinking about problems we meet subsequently. We call such examples, capable of heuristic use, POWERFUL IDEAS. This chapter documents a child’s introduction to a specific powerful idea in a computer environment. We trace his extensions of that idea to other problem areas, one similar to his initial experience and one more remote.
Introduction
The new availability of computer power to children in schools poses forcefully the question of the computer’s role in education. Here we present a case study of computer-based learning that goes beyond drill-and-practice and game playing to show how particular experiences carried a specific idea of general applicability into a child’s mind and how this idea was effective subsequently in his freely-chosen and self-directed problem solving. The stepping of variables — by which we mean the development of and the decision to apply a systematic mental procedure for isolating and incrementally changing one of several variables — is an idea of general applicability. Genevan psychologists have noted this idea as a very important one in that configuration which leads to the systematic thought of the adolescent (Inhelder and Piaget, 1958). The stepping of variables is the idea whose history we will trace in one child’s mind.
The subject of this case was Robby, my son, just turning eight years old at the time of the study. With his sister, Miriam, two years younger, he participated in an intensive six-month study at the Logo project of the MIT Artificial Intelligence Laboratory (see OCL and CECD.). Robby had visited the lab many times in the preceding years and had frequently participated in earlier studies. He brought to this work two mental predispositions which are relevant to what follows. First, he was inclined to call upon symmetry as a generative idea (this observation will be clarified subsequently). Secondly, his approach to problems was surprisingly systematic for one his age. (See Note 1, at the end of this text.) Such systematicity is not usually met until the age of ten or twelve years. Before we turn to the case material wherein systematicity plays its role, we must first present some folk-history on the procedures Robby encountered.
Polyspirals and Variables
Imagine that one day a child invented the “squiral” while trying to draw a square maze. The Logo turtle moves forward, turns a right angle, then repeats these actions, increasing the distance of the forward move with each repetition. In getting the angle ‘wrong’ while attempting a square maze, the child discovered that if the turtle turns through an angle near but not equal to 90 degrees a four-armed spiral emerges from the drawn shape (see Figure 1).
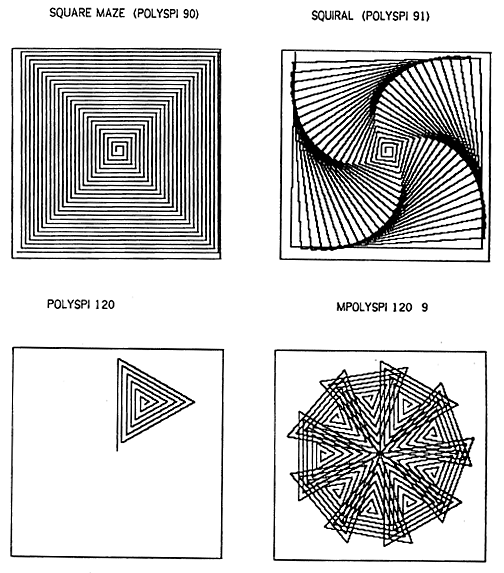
Figure 1
Basic Mazes and Squirals
Emergent effects such as this appear regularly in turtle geometry, and are very striking. The nature of the Logo language and the spirit in which students use Logo make it easy and natural for students to change programs in various ways. The ‘square maze’ and ‘squiral’ programs were modified, by students, to produce the “polyspi” (short for polygonal spiral). The actual Logo program that produces these figures is as follows: (See Note 2 at the end of text.)
TO POLYSPI
FORWARD :distance
RIGHT :angle
MAKE “distance (:distance + :delta)
POLYSPI
END
The general meaning of these Logo commands can be inferred from the example. Details are not important for the purposes of the present chapter, except to note that “distance, “angle, and “delta are variables, and must be initialized. This means that the computer must somehow be told what number to associate with the named variables “distance, “angle, and “delta. The fifth line in the POLYSPI listing is of special importance. The procedure POLYSPI calls on itself! A feature of the Logo language makes this possible. Notice, however, that before calling on itself, the procedure has changed the value of one of the variables; this is done in the line:
MAKE “distance (:distance + :delta)
Consequently, the result of POLYSPI calling itself is to execute the procedure another time with the value of the distance variable incremented; the procedure stops when the turtle goes off the edge of the display screen. A number of the designs produced by the POLYSPI procedure from the near- regular polygonal angles are very pretty. The emergent effect of such designs can be compounded, as by a procedure I composed, MPOLYSPI (short for multiple polyspi), to make even more complex and attractive designs (see the triangular POLYSPI and its nine-fold compounding in Figure 1B). Emergent effects in turtle geometry cover a range which permits mutual engagement and learning by both children and adults — and thus they became a topic of exploration in many of the research sessions Robby and I spent at the Logo lab.
Robby’s introduction to variables went forward in several small steps. Initially we played games with a set of labelled match-boxes and card- written commands for changing or examining the contents of the boxes. We presented the image that global variables were functionally like little boxes with contents that one could examine and change by commands of the Logo language. Consequently, Robby’s first use of polyspi procedure involved a “set- up” procedure whose functions were to clear the display screen of the previous design and to permit his keying of initial values for “distance, “angle, and “delta. Subsequently, we explained “input variables” as a keying convenience which permit an integrated set-up procedure. The form of the “polyspi with input variables” is this:

Figure 2:
Multiple Polyspirals: a Shape Family
TO POLYSPI :distance :angle :delta
FORWARD :distance
RIGHT :angle
POLYSPI (:distance + :delta) :angle :delta
END
(Here the incrementing of distance is implicit in the polyspi self invocation.)
Ideas and Families of Shapes
A primary intellectual challenge in exploring polyspi designs is how to impose some comprehensible order on their considerable variety. Notice, now, that the polyspi procedure with a zero value for delta will draw polygons. For such polygons drawn with angle values dividing evenly into 360, the polygons are regular and closed; after turning through 360 degrees, the turtle retraces its original path. In second grade, Robby had learned the names of some geometric figures and the number of their sides. For example, he knew that a regular hexagon has six sides. When the input angle is that of some closed polygon, e.g. 60, the polyspi procedure with small positive values for delta draws figures we called “mazes”. We distinguished between such mazes and other shapes. Robby and I together produced a “family of mazes”, i.e. a collection of the regular polygonal spirals with three through eight sides. We printed these designs and displayed them on the wall. My intention was that individual members of this series of figures could serve as “anchors” for further exploration, both connecting to Robby’s previous knowledge of geometric forms and serving as reference bases from which other shapes could be seen as variations.
A Didactic Introduction to Shape Families
In the next Logo session on this theme I presented explicitly the objective of developing “families of shapes” and showed Robby several examples of such shape families. The first, reproduced in Figure 2, shows six shapes made by incremental change of the MPOLYSPI 122 “folding factor” from one to six. Thus the single sub-figure, a POLYSPI 122, is repeated an additional time in each of the five successive designs. Similarly, a second example of a shape family (not shown) displayed changes in the six-fold MPOLYSPI 122 as the value of delta was reduced from seven to one. The “lesson” I professed with these examples was that focussing on the systematic changes of a single variable was a fecund method for understanding the results from the complex interaction of several variables. Whether or not Robby accepted my “lesson” or used what I showed him in another way is an issue we will discuss subsequently.
The Child Exploring the Space
Robby had the opportunity to construct his own shape family. (I had been careful to leave him the most interesting variable for his changing.) I proposed building a shape family around one of the mazes as an anchoring value. Robby selected the hexagonal anchor and enthusiastically created and printed the designs of Figure 3, then hung them in order above his desk. In subsequent sessions, he constructed a shape family anchored at ninety degrees, first increasing the angle value and later (beginning at eighty-five degrees) approaching the anchor from below. This concluded the didactic phase of Robby’s introduction to shape families.
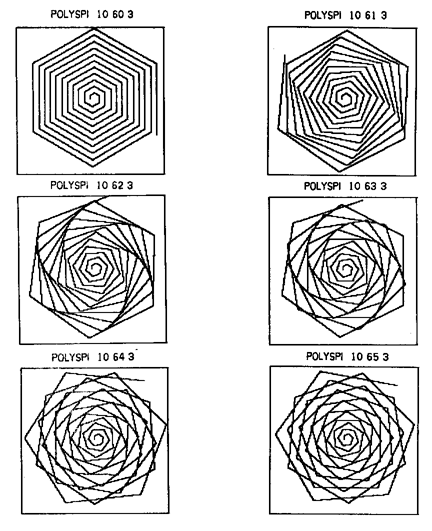
Figure 3:
A Hexagon Based Shape Family
A Polyspiral Variation
The increment input to the POLYSPI procedure (the variable called delta) is applied to the first of the two other variables, “distance and “angle. What happens if delta is applied to augment angle instead of distance? Few people have any intuitive answer for such a question and most become easily confused in trying to imagine what design would be created. With small values of delta (and with an initial angle of zero), the turtle will move off in one direction and gradually spiral into a node. (For this reason, the procedure was named “inspi” by its originator, Marvin Minsky):
TO INSPI :distance :angle :delta
FORWARD :distance
RIGHT :angle
INSPI :distance (:angle + :delta) :delta
END
(See several examples of basic Inspi designs in Figure 4.)
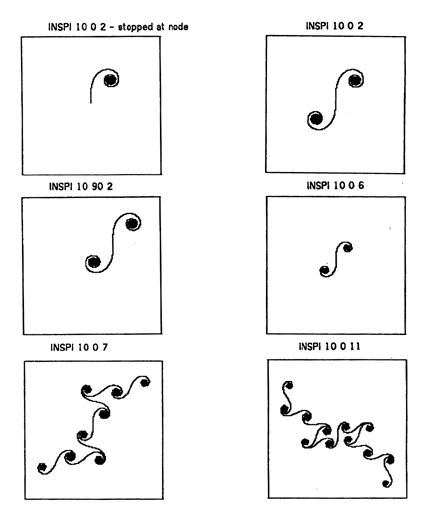
Figure 4:
Six Drawings Made by the INSPI Procedure
The Subject’s Initial Inclination
When he was first introduced to inspi designs, Robby’s inclination was to vary “angle. After trying INSPI (10 0 2) at my direction, he executed INSPI (10 90 2). (The effect of these input values, shown in Figure 4, is to alter the center location and orientation of the design.) When I tried to discuss changing other variables, Robby’s personal agenda came forward in comments such as these: “Hold it, Dad, all I want to make it do is go the other way”; “I want it in the exact same direction, but opposite.” After a few false starts, I followed his lead:
Robby: How do you get it to go the other way?… It goes right. I want to make it go left.
Bob: We’d have to change the A procedure (we had renamed inspi A because it changed angle values).
Robby: Why don’t you make a B procedure, to make it go the other way?
Bob: Why don’t you?
Robby: [a complaint] I don’t know how!
Bob: You copy the A procedure, but where it says “right” you change it to “left”.
After creating the symmetrical procedure, Robby still inclined to vary “angle. I intervened to focus his attention on delta as a possibly potent variable, but he could not be interested at all. When he refused to follow my forceful suggestion to execute INSPI (10 0 7), I did it myself with those inputs and had the satisfaction of hearing him admit, “I wish I had done that.”
Symmetrical Inspi Designs
Robby now began to make the symmetrical inspi designs of Figure 5, using his B inspi procedure with inspi procedure A. As the complex symmetries of the two-fold INSPI (10 0 7) developed, he exclaimed, “Isn’t that wild!” I offered 11 as the next delta candidate. After printing out the second symmetrical design, I proposed (would that I had bit my tongue) this speculation:
Bob: Why don’t you try the next prime number? It turns out — and I never would have guessed it — that prime numbers —
Robby: [interrupting] Do this? [referring to the symmetrical INSPI (10 0 11)]
Bob: Why don’t you give 13 a try?… I’m not quite sure, but that’s my speculation, anyway. I’m sorry I told you that. Maybe I should have let you have the chance to figure that out.
Robby: Yeah… but I don’t know the prime numbers very well.
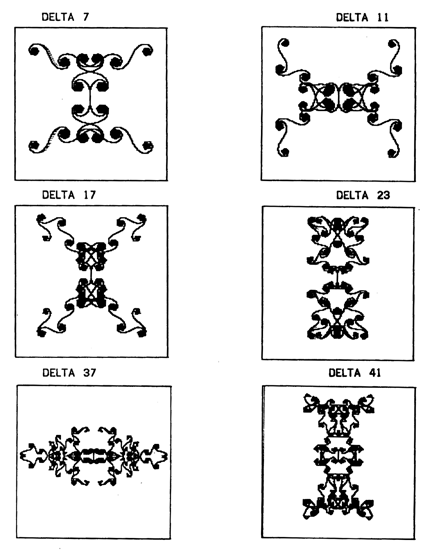
Figure 5:
A Selection of Robby’s Symmetrical INSPI Designs
Understanding and Delight as Motives
After executing the symmetrical INSPI 13’s, Robby concluded, “Every time we do it, they’re getting super-er.” We conclude that Robby’s strong confidence in the heuristics of pursuing symmetries in design was amply confirmed. This use of a heuristic is one clearly focussed on the objective of generating interesting designs. If there were any motive to understand better these inspi designs through symmetry it must have been relatively insignificant compared to his delight in creating them.
Self-direction and Taking guidance
My uncertain speculation that primes had something to do with creating interesting designs inspired Robby to produce a complete set of symmetrical inspi designs for all the primes between seven and fifty. (See note 3 at the end of this text.) One might imagine he took my advice because he is a suggestible boy and easily led. The opposite is more nearly true. Two examples stand out. At my direction, he tried some large-value deltas. When I called his attention to the puzzle of the minimal design (a small straight line) made with the initial angle zero and delta 180, Robby continued from there with elegant symmetrical designs, based on delta values of 187 and 206, then decided, “I think I’ll go back to using primes.” After producing designs for delta values of twenty-nine and thirty-one, he decided that thirty-three was not a prime and rejected it as a candidate value.
Knowing that thirty three would produce an interesting design, I pushed him to try it, but he refused. “No, I’m going to use only primes.” He then figured out the values of primes thirty-seven, forty-one, forty-three, and forty-seven and completed his own creation — the family of symmetrical, prime-based inspi designs.
What do we make of this material?
Most obvious is that the world of experience confirmed the value of Robby’s heuristic, “try symmetry,” as a generator of pretty designs. Second is that even though the inspi procedures led to results less intuitively accessible than those produced by the polyspi procedures, Robby explored this world of inspi designs in a systematic way that amounted to a first extension of the idea of variable stepping. That is, Robby settled on delta as the most potent variable for these designs and followed my “prime hypothesis” to generate the next candidate delta value for creating a design. I believe we can infer that his experience of this inspi world confirmed the value of stepping variables as a heuristic.
Learning a Heuristic
The symmetry heuristic is good for generating designs; what is stepping variables good for? Did Robby appreciate this as a second heuristic for generating pretty pictures or did he see it as a way of organizing the world to understand it better? This distinction is one that we make, one that we might call upon in judging a possible claim that Robby learned a heuristic that is good for some specific purpose. I believe rather that Robby learned a heuristic that was specific with respect to activity but vague with respect to purpose. Although he may have begun to apply the heuristic to generate interesting results, his ability to select and order them through the ‘prime hypothesis’ helped define what was interesting about them. The final outcome for him was the better comprehension of something worthwhile understanding (in terms of his judgment of what was worthwhile). This point is illustrated in the final incident reported here.
Beyond the Laboratory
Because Robby lives with me, it has been my privilege to observe how these experiences at Logo were reflected in his later problem solving. Some six months after our study at the Logo project, a parent visiting his third grade class introduced to Robby the “paper-rings puzzle.” This bit of topological magic leads to the “squaring” of two circles. (It is a puzzle in the sense of creating a surprising result.) I recommend you try it. Here’s how it’s done:
1. Cut two paper strips of equal length (eight inches will do).
2. Draw a line down the middle of each.
3. Bend each strip of paper into a circle and tape the juncture.
4. Join the circles at tangents perpendicularly and tape the juncture.
5. Cut around the middle line drawn on each circle.
When two strips of equal length are so connected and cut, the surprising result is that the strip-halves end up taped together as a square.
Re-play
Robby enjoyed this activity when shown it. Several days later, I removed a pattern of strips he had made from a paper on my clip-board. When I interrupted his reading to give him the sheet of paper, Robby recalled the game and quietly took it up on his own. He was very happy when the procedure produced a square and showed it to his mother and me. We neither paid much attention. Going on to three circles, Robby cut two of the three along their mid-lines. He judged (in error) that he had finished by finding a square with a bar (a double-width strip) across the center. It lay flat. Still no one paid attention. He went on to four circles. When he cut all the mid-lines, what he got was a confusion of flopping paper strips. I advised him to try getting it to lie flat. He was delighted when he achieved this goal and subsequently taped the paper strips to a large piece of cardboard. The resulting shape is this:

Figure 6:
the “paper-rings” puzzle
Elaboration
But why stop at four? Robby went on to cut and connect five circles. When cut, the five circles separated into two identical non-planar shapes. He taped these to another piece of cardboard. On trying to tape the floppy figures made from cutting six rings, Robby succeeded with great effort. He decided the problem was getting too complicated to be fun and quit.
When I recalled his attention to the figure made by cutting two of the three circles and pointed out that the middle bar of his figure was double-thick, Robby agreed he had cut only two circles. He saw immediately that this square would divide into two rectangles. “The five’s made two too. Hey! I’ve got a new theory: the odd-numbered circles make two and the evens all stay together.” Robby could not prove his conjecture, but in the course of one discussion when I asked how he had gotten the idea of this exploration, he explained, “Dad, it’s just like what we did at Logo with the shape families. I changed one thing, a little at a time.”
Mixed Purposes —
Robby’s explanation witnesses that he conceived of his exploration in terms of that past Logo experience. This does not imply that the Logo shape families marked his first encounter with or use of the idea of controlled changing of a single variable. We may infer, nonetheless, that he owned an example of this idea crisply applied to a complex but comprehensible range of interesting phenomena, and further, that it did provide him guidance for thinking about a problem met subsequently. He appreciated his Logo shape families experience as embodying a powerful idea.
Did he apply the heuristic because it might generate new results or because it might help him understand a range of puzzling phenomena? We can not profitably make such a distinction if his purposes were mixed. The two aspects of purpose we might choose to distinguish appear to have been inextricable for him. He used this powerful idea as a heuristic for orderly exploration to generate interesting results in a comprehensible way.
What Follows ?
We have come to the end of this story, but the question remains “where does this powerful idea of variable stepping go from here?” We find a hint in the discussion of Robby’s new theory. His conjecture, that the odd-numbered chains make two separate figures, was based on the regularity he observed in five cases (with two through six rings).
When I asked him to prove this new theory, his method of choice was empirical — he constructed a seven-ring puzzle and cut each of the rings. (I did not suggest his doing so. I wanted him to reflect more.) He clearly expected the seven rings to separate into two figures and took their doing so as proof of his theory. What is significant in this observation is the way hypothesis testing emerged as a minor variation from a preceding activity which was a theory-free but orderly exploration of an interesting domain. Variable stepping had become for Robby a way of approaching the world, of seeing ‘what’s what.’ The power of the idea — as witnessed by Robby’s quick invention of his new theory — is that from ‘what’s what’ ‘what follows’ is ‘intuitively obvious.’
Publication notes:
- Written in 1980.
- Published as MIT AI Memo #590 and Logo Memo #58, July 1980.
- Re-published in The Journal of Mathematical Behavior, 1982, Vol. 3, No. 2.
- Republished as a chapter in Computers and Cognition, Lawler, DuBoulay, Hughes, and MacLeod, John Wiley, 1986.
Acknowledgement:
A discussion of this material with Gary Drescher helped to clarify some issues touched upon in this text.
Notes on the Text
- For example, at age 7;8;8 on Piaget’s “bead families” task (Piaget and Inhelder, 1975), after attempting to arrange combinations of five things taken two at a time by an empirical procedure, Robby spontaneously started the task a second time, grouping his bead couples in five groups by the color of one bead and joining with each base-color bead another one of a different color.
- We signify references to variables by preceding them with quotes; executed procedures are referenced in capitals, and definitions of terms are enclosed in double quotes. ” :” is an operator in Logo which means “give me the current value stored for this variable name”.
- The apparent complexity of an inspi design is determined by the sequence of values of the angle variable. Most significant is the remainder left when the increment value is divided into 180 and 360. As the simplest example, consider the case where the initial value of “angle is zero and “delta is ten. After some iterations, the turtle will turn right through this sequence of degrees [170 180 190]. RIGHT 180 turns the turtle around completely. RIGHT 190 is equivalent to LEFT 170. Thus, at the first node, the turtle begins executing steps which invert, in reverse order, each preceding step. Since ten divides into 360 with no remainder, we can see that there will be another node at an “angle value of (180 + 360) degrees, after which the turtle will once more retrace its path. The primes are merely a subset of the numbers which don’t cause the turtle to retrace its path after the second node.
