LC1bA5 ^
from Computer Experience and Cognitive Development
see also Cognition and Computers: studies in Learning
 |
 |
The Development of Objectives
…the more one examines life the firmer becomes the conviction that it
contains no well-rounded plots and that a good deal of what we do has a
higgledy-piggledy nature, slapstick in tone, which forces us either to be
greatly sad or highly hysterical. Philosophy is merely the parlor
interpretation of unplanned pandemonium in the kitchen. The philosopher
attempts the Herculean when he tries cataloging chaos.Walt Kelly
from the Epilog to “Ten Ever Lovin’ Blue Eyed Years with Pogo”
Introduction
This text explores a person’s developing objectives, tracing the
pattern of their changes through analysis of a limited empirical corpus. The
issue confronted here is creativity in respect to objectives. That goals
dominate activity is a central dogma of current work in the study of
intelligence. However, any person who showed the goal commitment typical of
artificial intelligence programs would be judged a monomaniac. Human commitment
is typically of a more limited sort. Consequently, I prefer to describe people
as having not goals but objectives, indeed, large collections of objectives. [1]
In special circumstances some people do develop
commitment to and struggle to achieve very difficult ends; such behavior would
be properly characterized as goal driven.
My specific endeavor here will be to recount and explain some details of how a
seven year old child drew the picture of a house and its setting. My general
purpose is to find and present specific sources of guidance, i.e. what led the
child to do one thing rather than another. The two principles of creative
projection I uncover and examine are simple elaboration, that is, applying some
working procedure to some slightly more complex case, and objective formation
proper through the frustration of an attempted elaboration. Tracing the
developing activities of the project raises important issues about how problem
solving in the current task domain relates to earlier experiences. The value of
working through this analysis and its introductory material is uncovering a
view of mind which has been applied to the problem of studying learning in
my subsequent research.
Background Of The Data Collection
I had two purposes in preserving a better record of interactions with
children, first to understand better the specific path of learning and second
to record their reactions to programs I developed for their use. The work was
not an “experiment” in the sense of being fashioned to test some hypothesis.
This particular project began with my asking my son, Robby, aged 7 years 5
months, (7;5) that he test a new drawing program and give me his reactions.
(See Figure 1) At the end of the project, I had an audiotape record of a
multi-day computer project. The material is suitable for an analysis of
objective development because the boy followed his own direction within the
loose constraints set by the computer medium and the programmed environment.
The story of how Robby made this drawing will not be presented chronologically
but rather in an order chosen to highlight the ideas which the case material
exemplifies. We begin with presentation of several related and simple cases of
elaboration and the natural limitations of the process. Let us start then with
a simple idea, but in the middle of a story.
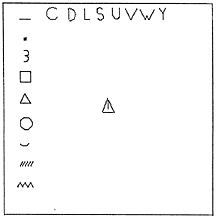
Figure 1: a menu of shapes
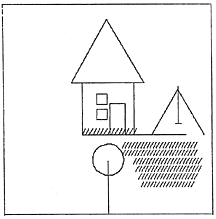
Figure 2: H7GS, “house and seven grasses”
Cases of Elaboration
The Basic Example|
Near the completion of the drawing shown in Figure 2, Robby said he
wanted to put some grass near his house. After several trials, exploring the
effect of the input parameters on the turtle’s action, Robby completed the
first line of grass at the base of the house. He then undertook the yard,
first with three lines of grass (after which he saved his work as H4GS — House
and Four Grasses) and then completed, with three more lines of grass, his final
product, H7GS. In the explication of changes in Figure 2, notice the
stepwise progression and changing of one element at a time.
In this environment, elaboration is the process of repeating the execution of a
successful procedure with some small variation of its application, for example
in the location of the turtle or the value of an input variable supplied to the
procedure. With the grass of H7GS, the
process of elaboration was terminated by exhaustion. There is no more room for
grass; in this specific sense the application of the procedure to this little
task domain is complete. The child’s progressive mastery of the use of the
procedure in the environment has turned a procedure, at first successfully
executed in one specific case, into a tool usable more freely within a small
domain of application. This is a very concrete form of generalization. Such a
process of elaboration is not limited to task domains using computer
procedures. For example, if one tells a child that numbers greater than twenty
are formed by concatenation of twenty with the well-known smaller numbers, he
should not be surprised that the child puts together what he’s been told and
begins counting with twenty-one and proceeds through twenty-nine, twenty-ten,
twenty-eleven, etc. With this counting example, the child focusses on the most
salient element and varies the adjunct terms. Although “achieving mastery
through consolidation of a working procedure” may be one reason behind the
everyday phenomenon of elaboration, there are surely others. I am less
interested in reasons for elaboration than in the creativity of the process.
Consequently, I choose here to set out some other examples which reveal the
impact of concrete experiences on the process.

Figure 3: Paper Plans
Repeating a Successful Procedure to Achieve a Complex Concrete
Objective
Early in the project, Robby noted some of his intentions in the sketch
of Figure 3. In general, his plans revealed a process of repeating a
successful procedure with a minor variation to achieve a richer, concrete
objective, one more complex, more full of detail, more like the everyday world
in which he lived. For example, the house he first produced has overhanging
eaves as did the carriage house in which we lived at the time. The dormer
windows — a dominant aspect of his planning — reflect forcefully the
influence of the presence of such windows in that house, as well as being
duplications with reduced proportions of the HOUSE itself. The detail of the
windows — their being made of four panes — also reflects this casual
inspiration of the created object by the concrete experience of everyday
life.
Blocked Objectives
I felt it necessary to dissuade Robby from undertaking these specific
additions to his house because of all the complicated positioning that would
have been required to achieve the dormers-with-four-paned-windows. He himself
decided that making a doorknob for the door would be too tedious (he imagined
here making a series of twenty four “forward and right” commands). Finally, the
grass which he later added as the finishing touch of his H7GS design first
appeared in this sketch (the five slanted lines with three arrows from them).
I suggested to Robby using the HAIR procedure to make the grass he wanted.
Robby adopted the idea and elaborated it: “I could put three grasses in here
so it looks like a yard.”
If objectives are blocked, some appear to be lost but not all of them. We know
from the final design of figure 2 that Robby ultimately achieved his
objective of making a yard. The characterization of elaboration as one process
of objective generation is accurate, but it is not the whole story. We now
examine in detail how this simple objective of making a yard became deferred
and by what sort of objective it was replaced. The reason we do so is to
develop a richer sense of the interplay of multiple objectives over a long time
scale and, hopefully, a simple model which adequately describes that
interplay.
Deferred Objectives
After I explained how to use two input variables to specify the height
and width of a door, Robby expressed a desire to make a park, “Before we go
into the fancy stuff, why don’t we put in the grass.” He pointed to his chosen
design in the shape menu, and I told him the procedure name was SAW. Neither of
us knew what relation the specific input bore to the size of the figure. Robby
decided to execute SAW [10]. The object created was a single sawtooth of size
smaller than the turtle-cursor. He erased that and tried, at my suggestion,
SAW [100]. Robby wanted grass extending from the house to the edge of the
screen. What he got surprised us both.
Robby: Hey! That’s one big blade of grass.
Bob: Oh… you know what happened, Rob? This SAW procedure tried to make
the grass 100 turtle steps high. That’s not what you wanted…. I think you’d
better erase that…. Go ahead, Rob, rub it out.
Robby: No, it’s going to be a playground.
Bob: Oh… I get the idea. [This is not a suggestion, but my empathetic
grasp of what his motives were.] You want to keep that, like the swing set out
back in Guilford [the town we formerly lived in].
Robby: Yeah.
Bob: We can still put some grass in.
Robby: No. It’s going to be a tar playground.
The tenacity with which Robby protected this accidental addition to his house
was shown even more forcefully in what followed. He could not see any good way
to get the turtle to the top of the “swing”, save trial and error. I suggested
erasing the swing and re-creating that appearance by executing TRI [100],
because I knew that the turtle would finish the procedure aligned under the top
vertex of an equilateral triangle. From such a position, reaching the vertex
would have been simple. Refusing this suggestions, Robby proceeded to the
vertex by moving and turning the turtle little by little, reaching it precisely
but in his own way at his own pace. Thence he drew the swing and seat of
Figure 2.
Demon Procedures and the Symbolic Achievement of Frustrated Objectives
Robby’s adoption of adding a swing to his house can be described as the
activation of a demon procedure. In the lexicon of Artificial Intelligence,
“demon” names a procedure which becomes active under the fulfillment of
specific conditions. Think of Maxwell’s demon, a little man who watches a
strictly limited set of conditions and leaps into action when those conditions
indicate the opportunity is right to effect his objective. Robby’s “swing
demon” was created by our moving to Massachusetts. At our former home, the
swing set was Robby’s delight. When we moved, he expected to disassemble it
and bring it with us. The unforeseen obstacle was the resistance of our new
landlords; they would not permit such a swing on their property.
I propose, then, that Robby’s adding a swing to the HOUSE he had constructed,
when he saw its achievement as being within reach, amounts to a SYMBOLIC
REALIZATION of a prior, frustrated objective. I specifically disavow making
the Freudian claim that such symbolic realization satisfies whatever
frustrations are entrained in an objective’s failure.
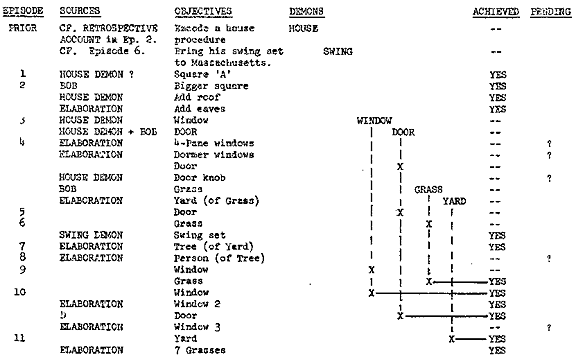
Figure 4: Inception and Fulfillment of Deferred Objectives
My proposal is
different, that the symbolic realization of prior frustrated objectives
explains a significant portion of those everyday objectives which a person
adopts as he operates in a relatively unconstrained task domain.
The Demon Objectives Proposal
This proposal — call it the DEMON OBJECTIVES proposal — implies first
that there might be a multitude of objectives which could be activated at any
time. This is very troublesome. One might ask whether it be possible to make
any sense at all of behavior — in terms of the operation of such demon
procedures — given their potentially enormous number. It IS possible to do
so. Figure 4 exhibits such an analysis in detail of the components of the
design H7GS.
The Demon Objectives proposal is troubling most especially because with the
“symbolic realization” of objectives almost anything can symbolize anything.
Such vagueness is possible that any interpretation might work. It is at this
point that I must invoke a commitment to empirical detail as the guidance which
can save us from the excessive fancy of a theorist’s imagination. If one
examines what is unusual about the interpretation of objective formation
implicit in Figure 4, he will notice that it depends especially on two
factors: first is the unusual closeness, in a problem solving study, of the
experimenter and the subject (no non-intimate of the subject could claim such
understanding without ridicule); second is the time scale as a factor of
enormous significance.
To clarify the importance of time scale, I present here a second demon driven
interpretation of objective formation, one based on related material from a
protocol taken in an earlier project with the same child. It also introduces a
new issue of major importance. Robby’s attempting to apply a successful
solution to the next more complex objective in that earlier project encountered
an unanticipated obstacle and generated a demon — an objective he failed to
achieve and which was deferred for activation at some later time. I propose
that Robby’s choice of drawing a house as his initial and primary objective in
H7GS derives from the following specific failure in a previous project.
A Retrospective Account – A House that Failed
I told Robby I was going to make a procedure for him to try on his next
visit to the Logo lab. I wrote TRI, a procedure for generating an equiangular
triangle of 100 turtle steps on a side. [The Logo procedures encoded throughout
the text conform generally to that of Apple Logo. Where departures are made (usually
for historical reasons), I will make it clear. Since Logo is a high level language, the differences
between various implementations with comparable machine features are minimal.]
Robby was a little confused as to my purposes but followed step-wise my
drawing the figure on our chalkboard and my encoding the procedure on a 3×5
card. I followed TRI with TINY, which drew a similar triangle of 30 units side measure.
| TO TRI | TO TINY | TO FOX |
| FORWARD 100 | FORWARD 30 | CLEARSCREEN |
| RIGHT 120 | RIGHT 120 | SETHEADING 90 TRI |
| FORWARD 100 | FORWARD 30 | LEFT 60 TINY |
| RIGHT 120 | RIGHT 120 | RIGHT 60 FORWARD 70 |
| FORWARD 100 | FORWARD 30 | LEFT 60 TINY |
| RIGHT 120 | RIGHT 120 | HIDETURTLE |
| END | END | END |
Thereupon I told Robby the idea was to make a FOX out of these two triangles,
in the way he had learned from reading Ed Emberley’s books. This caught his
interest. We began FOX. [Employing the figure assembly techniques described in
Ed Emberley’s books, Robby’s practice was to make elaborate and extensive drawings at
nearly every opportunity. His figure assembly skills were well developed.] We simulated on our
home blackboard the action of a Logo computer turtle. I arranged initial
conditions so that at the completion of TRI the turtle was horizontal at the
left vertext, pointing across the top of the head. To put on the ear we had to
have him point differently. “How much is half of 120”, Robby asked me, then
said the turtle must “LEFT TURN 60” after my answer. What do we do next ?
Robby: “TINY”. His decision to turn left 60 degrees worked. The FOX had one
ear. We returned the turtle to the horizontal, went forward 70 turtle steps,
did a left turn 60, and invoked TINY. Our FOX was complete. Robby showed his
mother the procedure we had ‘planned out’ for our next trip to Logo and brought
her to the chalkboard to see the FOX we had drawn. My objectives were
completed, but Robby developed his own.
An Unexpected Elaboration
Robby asked me for a 3×5 card so he could write a procedure for a HOUSE.
It is hard to be certain why Robby chose a house as his next project, but it is
not unreasonable that, having worked through a FOX picture by assembling two
triangles, Robby was attempting to create a house from a triangle and a square.
One could judge this objective to be the next more complex task, thus a simple
elaboration. I tried to help, but Robby said he wanted to do it alone. As I
was leaving the room, he asked how much was half of 90. This question echoed
his earlier query when attempting to figure out how much the turtle should turn
before drawing the TINY ear. Half of 120 was, by chance, a good choice in that
case. Half of 90 was not so lucky a choice in this second case. When I
returned from some chores, I found on the chalkboard this triangle, with Robby
standing puzzled before it.

Robby’s Triangle
Drawing of a House That Failed
Robby asked if 40 was the right length for the slope of the roof. I
informed him that by choosing 45 degrees at the horizontal vertices he had
gotten himself into a tough problem — not even I could tell him what the right
number was just by looking at the triangle. He argued that 40 should work
because “when you make triangles out of tinker toys, if you use two blue ones
for the side, you use the next bigger size, a red one, for the longer part; and
50 is like the next bigger size from 40”. Should I have told him about the
square root of 2? I did say that with triangles, the next bigger size for the
side depends on the angle, that 45 degrees made things tough but that 60
degrees was a good number and that’s why the FOX had worked out so well. Robby
was clearly in over his head. He decided he was going to stop because the
problem was too hard and he had to leave for a birthday party. He folded his
work and threw it in the trash whence I retrieved it later. You can see his
drawing of the house he failed to encode in Figure 5.
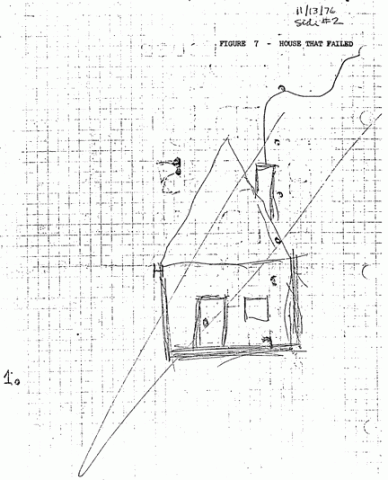
Figure 5: A house that failed.
Shadow Domains – a Central Postulate of This Work
In this incident, one can see exhibited the guidance of problem solving
within the task domain (Logo programming) by values appropriate to what I call
a “shadow domain”. Logo commands are typically formed by an operation (WHAT to
do) and an operand (HOW MUCH of it). Note that Robby had a good sense of
operations in that domain. He knew about going forward, about turning, about
making procedures, but his use of these ideas was imperfect, in the sense of
how to apply them to this specific problem. What recourse had he? He chose to
operate in the task domain with operand values derived from the shadow domain,
as his explicit analogy makes clear: he assigned distance values in this new
domain, Logo language programming, on the basis of relations applying in a
shadow domain, in this case the play world of tinker toys, to which he
assimilated his coding judgments. Should this surprise anyone? Is not an
operand — the how much or how many of an action — the finer specification of
choosing what is to be done? If one is familiar merely with the operations of
a domain, is it not reasonable that judgments of quantity and relation might
still lag behind familiarity with operations? In precisely this sense and at
such a specific point, the values of a shadow domain could be used to guide
judgments in a task domain.
To understand problem solving in a task domain, one must be sensitive to
existing shadow domains — whatever they are and however many they may be.
There exists some more profound relation that must be considered in the problem
solving environment than a simple assignment of external objects to internal
categories. This more profound relation is an expression of the fundamental
problem-deforming character of mind. The impact of such guiding knowledge on
problem solving MUST be considered and CAN be considered; THIS IS A CENTRAL
POSTULATE OF MY WORK. Let us now attempt a deeper characterization of these
shadow domains and the development of objectives.
Reflections
Shadow Domains and Cognitive Structures
We have seen how this little shadow world of “tinker toy” play entered
into one child’s problem solving in a programming task domain. One could
label such a thing analogy and let it go as something vaguely understood. I
choose, however, to pursue the character of such shadow domains by a more
extended analysis of this example. Consider first that the guidance of problem
solving solving by past experience CAN ONLY BE through the cognitive structures
of mind. The child has constructed within his mind symbolic descriptions of his
past little worlds of experience — call such a structure a microview [2] —
which is useful not only in tinker-toy play but also as a model which
provides guidance to him for solving newly encountered problems in different
task domains. Three characteristics of this tinker toy microview stand out as
especially noteworthy: the concreteness of the objects of the world; the
usefulness of the knowledge about them for guiding problem solving; their
procedural genesis.
With respect to concreteness, note that the rods not only have well defined
properties of length and assembly-relations, they are also specified by their
color coding. The salience of such accidental properties as color (for objects
whose most important relations in normal play use are geometrical) implies that
microviews may be more experience bound and particular than is logically
necessary. An implication of this fact is that the use of such microviews with
particular problems encountered may be highly idiosyncratic. If the child
preserves too much concrete detail of his past experiences, his problem solving
attempts could be more hindered than helped by such guidance. Is not this all
too often the case ?
The Generation of Hypotheses from Simultaneously Active Microviews
The use of one body of knowledge, e.g. the tinker toy microview — to
provide explicit guidance in problem solving in a different task domain,
programming in turtle geometry, emphasizes its model-like character. Robby
called upon his knowledge about tinker toys — and that of number sequences
simultaneously — to form an hypothesis about what might be reasonable operands
for turtle geometry commands. At least two observations are appropriate here.
First, such a style of problem solving helps explain the genesis of hypotheses
in fact, whether or not one can feel logically entitled to use the information
[3].
This observation raises serious questions about the value of any description of
problem solving which focusses on a single task domain. If shadow domains play
an important role in problem solving, if the invocation of knowledge
appropriate to the microviews constructed from earlier experience guides
problem solving behavior in novel situations, any study of problem solving
sharply focused on a task domain alone is vulnerable to the criticism that the
task itself may inhibit the characteristic operations of natural intelligence.
Secondly, if new microviews are constructed within the mind through problem
solving experiences and if the shadow domains of prior microviews guide problem
solving behavior in novel situations, can it be doubted that there must be a
very potent “genetic” influence of prior experience on the development of new
cognitive structures?
This in turn suggests that it might be fruitful to think of the mind as having
a control structure of invocable knowledge which embodies the genetic path of
descent [4]
To the extent that any description of mind — however precise and formal —
cannot encompass such an organization of knowledge, it is inadequate to
represent human mentality even in the relatively simple area of problem
solving. Any theory which undervalues the functional and developmental
importance of such an organization of structures will misguide those who follow
it, no matter how great its other virtues may be.
Generalization and Classification
We can say a procedure becomes progressively generalized in application
as it is used first with one variation then another. Thus a concrete procedure
used within a task domain becomes a tool applicable over the range of that
domain [5].
But the microviews in the mind may be more than collections of procedures.
They have — or at least seem to have — existential implications. How can it
be the case that a procedure could serve a classificatory function? To the
extent that a procedure has become a tool which functions over a limited
domain, the question can be put to it whether or not a specific object would
serve a specific role in the functioning of the procedure. The question “Is X
a kind-of-thing ?” can be reduced to “Will X work in your procedure which
applies to such kinds-of-things ?” This is a commonplace question, one which
every problem solver asks when seeking substitutes caused by some material
shortage which blocks achievement of his objective with some ongoing
procedure.
Generalization and Objective Formation
Given that one can understand how a provided procedure such as SAW,
which Robby used for making grass, could be made into a tool through
progressive variablization of salient inputs, we might next ask how created
procedures such as HOUSE could also be turned into tools. The HOUSE procedure
is context-bound in the following senses. Consider the HOUSE as portrayed in
the picture of H7GS (Figure 2). That HOUSE is composed of a large square and
triangle with a door and two windows as essential features; call that HOUSE
‘HDW’ (for HOUSE-DOOR-WINDOW). ‘HDW’ does not exist independently of the
specific design in H7GS. For the HOUSE ‘HDW’ to exist as a tool, its
embodiment in a procedure would require extraction from the context in which it
developed as a construct. Creation of such a tool would show generalization as
context de-sensitization. Robby did not show this form of behavior. No one
should be surprised at failing to see such an event: one should expect such
generalization to take some time and to wait on the adoption of some objective
of greater scope wherein the development of such a tool would be
useful.
Context Desensitization
A second, specific sense in which the HOUSE is context-bound is in
respect of scale, i.e. the HOUSE, in however many instantiations it might
appear, would always be the same size. Let me exhibit some Logo instructions
to variablize a HOUSE, thus turning this object into a tool:[6]
| TO HOUSE.CONSTRUCT | TO HOUSE.TOOL :HOWBIG | |
| BOX [100] | BOX [ :HOWBIG] | |
| PEN UP | PEN UP | |
| FORWARD 100 | FORWARD :HOWBIG | |
| PEN DOWN | PEN DOWN | |
| TRI [140] | TRI [ (7 * :HOWBIG/5) ] | |
| END | END |
As an overview of the process of making tools from objects in this domain, we
should expect the developmental sequence to consist of at least these three
steps: creation of a concrete object for a specific purpose; context
desensitization of the procedure which produces the object; use of the
procedure as a tool by its invocation from a higher level of control. The
purpose, either explicit or implicit, of such an endeavor is to create
components for some project of larger scope — which could only be imagined as
possible given the achievability of its components.
Implicit in these forms of context desensitization, implicit in the repeated
use of a procedure as a tool, is the creation of structure through the
invocation of the procedure from a higher level of procedural control [7].
The Unified Generalization Proposal
I propose that the process by which a concrete procedure is transformed
into a tool is the same process by which a demon is created, that the failed
objective capable of symbolic realization is the cognate of the tool created
from the achieved objective. Let us call this idea the “unified generalization”
proposal. Let us look more closely at the parallel.
If one notices that any objective implies a structure, a temporal and serial
structure of the process of pursuing that objective. First, actions achieved
by procedures serve objectives. The structure of all actions have beginnings,
middles, and ends. The simplest such action structures, wherein the middle has
no significant complication, proceed nearly directly to achievement of the
objective. The simplest elaborations are of such a form. When that process
occurs (whatever it may be) which transforms the serial structure of pursuing
an objective into components of control structure, there is no reason to
suppose that objectives should be immune from the context desensitization that
is implicated in generalization. This is precisely what symbolic realization
of objectives requires.
If you compare the little procedures for the HOUSE.CONSTRUCT and HOUSE.TOOL,
you will notice that it is precisely the objective achievable by the procedure
that is changed. In this specific sense, the symbolic realization of a demonic
objective does not appear markedly different from the generalized application
of a procedure which has been transformed into a tool. At this level of
description it is possible to unify the problems of generalization and
objective formation. A schematic textual representation of the unified
generalization proposal is presented in the box of the caption.
Beginning:
An initial objective becomes active
— when its procedure appears achievable in a domain.
Outcomes:
The initial objective succeeds:
— this leads to a new objective through elaboration.
— the procedure becomes a more generalized tool.
The initial objective fails:
— this leads to a new objective through demon formation.
— the objective of the failed procedure becomes variablizied, that is,
symbolically realizable; as its furthest extreme, this permits detachment
from the local context and procedure which created it.
Consequences:
Any new objective can become an initial objective.
The range of a procedure’s efficacy is determined.
A Creative Closed System
A system such as represented in the box above is a creative, closed
system. Objectives proliferate, some to be achieved after deferral, others to
be permanently lost. Such a formulation shows how ideas and objectives may
develop in a specific way in an individual mind. Nothing implies, obviously,
that all objectives are determined exclusively by operations in such a closed
system. For example, different bodily needs can provide starting points for
diverse families of elaborated objectives (hunger, sex, etc.). Beyond the
achievement of objectives, there may also be other motives for mental action.
A second class might be represented by curiosity, seen as a primitive
inclination to explore imperfectly understood phenomena; a third class might be
purely expressive, as the poet G. M. Hopkins asserts:
Each mortal thing does one thing and the same:
Deals out that being indoors each one dwells;
Selves – goes itself; myself it speaks and spells,
Crying what I do is me: for that I came.
Constraining the behavior one examines by pre-setting objectives, as in typical
laboratory experiments, inhibits the surfacing of those processes which reflect
the nature of mentality as revealed through its self control. The kind of
analysis represented by the body of this paper, to the extent that it applies
to behavior less constrained than laboratory samples, is truer to the nature of
the mind. However unsatisfactory the conceptual machinery for coping with the
analysis of such challenges as Robby’s HOUSE, restricting oneself to simpler
problems will lead to solutions entirely inadequate to represent important
processes of the natural mind. If we fail to tackle such problems as Robby’s
HOUSE (which is constrained by the medium more than by any objective), we miss
a major component of mentality, perhaps THE major component. We might even see
demon-driven structures as a searching of domains so limited that nearly all
demons are inhibited. We might see isolated problem spaces constructed by
experiments. We will miss not only solutions, but also profound problems of
mentality.
How General Are These Ideas: “Bricolage”
One may ask, given that these notions are built on a few ideas and
illustrations, whether or not the characterization of mind is sufficiently
general to warrant interest and exploration. Against the goal-dominated
activities of programmed intelligence, I hold out a contrasting
characterization of human action, based on a much broader base of diverse
cognitive study than analyses of my children’s problem solving.
Claude Levi-Strauss describes the concrete thought of not-yet-civilized people
as bricolage, a French word naming the activity of the BRICOLEUR (a
man who undertakes odd jobs, a sort of jack-of-all-trades, or more precisely, a
committed do-it-yourself man). The essential idea of bricolage is the looseness
of commitment to specific goals, the idea that materials, structures, and
competences developed for one purpose are transferable, can very easily be used
to advantage in the satisfaction of alternative objectives. Levi-Strauss’s
appreciation of bricolage is sufficiently profound to be worthy of both
quotation and extended examination [8].
…The bricoleur is adept at performing a large number of diverse tasks; but,
unlike the engineer, he does not subordinate each of them to the availability
of raw materials and tools conceived and procured for the purpose of the
project. His universe of instruments is closed and the rules of his game are
always to make do with ‘whatever is at hand’….in the continual reconstruction
from the same materials, it is always earlier ends which are called upon to play
the part of means…. This formula, which could serve as
the definition of ‘bricolage‘, explains how an implicit inventory or conception
of the total means available must be made…so that a result can be defined
which will always be a compromise between the structure of the instrumental set
and that of the project…. The bricoleur may not ever complete his purpose but
he always puts something of himself into it….
Planning versus Bricolage
In this description, one can appreciate the opposition of planning (the
epitome of goal-directed behavior) and the opportunism of demon-driven
bricolage. This idea seems an idea profoundly antithetical to the goal-driven
commitments of cybernetics and artificial intelligence. Observe, however, that
the two are not discontinuous, that all activities can be seen as a mixture of
the dominances of the polar tendencies represented here. The second point, not
the less important, is that the relationship is not directional: there is no
reason to suppose that planning is a more nearly perfect form of bricolage. If
some inclusion relation must be sought, one could easily view planning as a
highly specialized technique for solving critical problems whose solutions
demand scarce resources.
Broader Considerations:
Control Structure of the Mind
Over the past century, we have witnessed a widespread abandonment of the
concept of “free will,” an idea useful to individuals and society but one for
which there is no sensible proposal at mechanical levels of description.
Theorists of mind have striven to replace the individual who directs his
thinking with some other alternative. Freud introduced fragmentation of the
person into three active and competing homunculi: the individual becomes the
body housing the Ego, Id, and Superego. For Freud, the apparently integral
personality is a projection by society and the self on the resultant behavior
of these three primtitive forces and their processes of interaction.
Minsky and Papert, in the “Society Theory of Mind,” push the fragmentation and
competition of the Freudian vision to its logical completion in the attempt to
banish from the mind any trace of a mysterious homunculus [9]. Instead of
three struggling fragments of self, they proposed societies of agents — each
agent so simple it could be represented by a comprehensible computational
process. For me, the image of mind as a society of computing agencies did not
make satisfactory contact with the issue of how a person can feel himself to be
related to the many subordinate processes from which others might see his
behavior to emerge. Levi-Strauss’s characterization of bricolage seemed to
fill this critical need — relating a computational theory to a more human
image of man — and to go considerably beyond it.
Bricolage as a Model for the Self-Construction of Mind through
Interaction
To the extent that bricolage, and not planning, is the best
characterization of objective-related human behavior in everyday situations,
introducing the idea of bricolage into the AI community could permit the
development of machine intelligence with some creativity in generating goals
[10].
But further, and much more importantly, if behavior is seen as driven by a
bricoleur’s objectives and if one constructs his own mind out of concrete
experiences, then the metaphor might be extended to bring Piagetian mental
self-construction (currently the best theory of human learning) within the
range of a non-demeaning mechanical vision of mind.
The Functional Lability of Cognitive Structures
Students of anatomy have named the adaptiveness of structures to
alternative purposes functional lability. Such functional lability is the
essential characteristic of the bricoleur’s use of his tools and materials. I
propose that bricolage can serve as a metaphor for the relation of a person to
the contents and processes of his mind. Bricolage, as a name for the functional
lability of cognitive structures, emphasizes the character of the processes in
terms of human action and can guide us in exploring how a coherent mind could
rise out of the concreteness of specific experience.
Bricolage presents a very human model for the development of objectives, for
learning, and even a model for the interaction of the texture of experience and
the symbolic descriptions through which people think. This represents not a
mere metaphor in some superficial sense but a radical idea [note 1].
Every new idea is a metaphor; what is important is its fecundity. An idea
becomes a radical metaphor precisely to the extent that its ramifications are
found to be richly productive, in practice, in other domains. Functional
lability is witnessed diverse other areas as well, for example in the process
of physical evolution, and in the development of civilization. Consider these
important examples.
Functional Lability — In The Evolution Of Flight
How did dinosaurs turn into birds? A team of researchers at Northern
Arizona University proposed an explanation for the development of powered
flight which appears to be a significant breakthough in our understanding of
this major evolutionary change [11]. It is valuable for my purposes as a
clear example of functional lability which emphasizes both the step-wise
adaptedness of precursors and the locus of creativity.
A number of people have believed that powered flight derived from soaring as
the membranes of tree dwelling gliders somehow changed into muscular wings.
The details of this scheme comprise the arboreal theory of flight. A competing
theory, the cursorial theory, has been much strengthened by the breakthrough of
Caple, Balda, and Willis. This team created a series of models of successive
forms of “proavis” and then established the progressive adaptedness of each of
these models by coupling appropriate aerodynamic arguments with a cost-benefit
analysis of specific behaviors. A sketch of their assumptions and arguments is
as follows.
The Physics of Running and Flying
Assuming first that the ancestors of birds were insectivorous dinosaurs,
the theory measures good adaptedness with the criterion of “foraging volume,”
the space within which the creature might capture bugs in a given time. The
greater the foraging volume, the better a creature could compete. Since
bipedalism produces a higher reach and speed covers a greater area, one or both
should be expected to develop. Well articulated, supple movement would provide
more effective penetration of that foraging volume, as would the ability to
jump at any point in a running course, so the well balanced control of movement
by itself would favor those creatures which possessed it. These issues of
balance and control become increasingly important as running speed increases.
The location of considerable mass in a biped’s forelimbs which could extend far
beyond the radius of the body would provide significant control. The conclusion
is that “wings” developed because of the adaptive advantage of better balance
in the air and on landing after a jump, not for flight.
Any flattening of these balancing forelimbs would provide lift [12], thus
permitting the extension of this increase in foraging volume through gliding on
limbs already powered to exercise control of attitude. A similar effect would
be achieved by extension of proto-wings through the elongation of scales and
their transformation into feathers. The effect of lift would be to increase
stability and thus permit greater running speed, and thus greater lift again,
both of which extend further the predator’s foraging volume.
Summary: Positive Feedback
In summary, three different physical changes lead to positive increases
in foraging volume; bipedalism, increased running speed, and controlled
jumping at speed. Because of the physics of the world, limbs extended to
control the trajectory during a high speed jump experience lift. Since this
lift increases with increasing speed and since it also increases the stability
of the running creature, a positive feedback condition develops where more
speed produces more lift and this in turn produces more speed. The creature
takes off. Once in the air, those very limb movements which facilitate
trajectory control, when coordinated, serve as the power stroke of flight.
Where does the Miracle Occur ?
The character revealed in this example of evolution is one where
opportunistic systems are constrained into paths of a step-wise development
which permit coupling of physical effects of the milieu. The magic comes from
the functional lability of physical structures (the leg becomes an arm becomes
balancing mass becomes an airfoil) in a world where serendipity is possible and
development irreversible.
Functional Lability — In The Invention Of Writing
The Sumerians of Mesopotamia are usually credited with being the first
people to write texts, about 3000 B.C. The writing system had two basic
character types: objects used as counters, numerical signs, were pressed into a
clay surface; all other signs, pictographs and ideographs alike, were incised
with the pointed end of a stylus. This invention is surely one of the central
events in the history of civilization. It is possible to advance well reasoned
arguments that make this creation comprehensible. More specifically, with the
domestication of plants and animals around 8500 B.C., as Schmandt-Besserat
observes:[13]
“The new agricultural economy, although it undoubtedly increased the production
of food, would have been accompanied by new problems. Perhaps the most crucial
would have been food storage. Some portion of each annual yield had to be
allocated for the farm family’s subsistance and some portion had to be set
aside as seed for the next year’s crop. Still another portion could have been
reserved for barter with those who were ready to provide exotic products and
raw materials in exchange for foodstuffs. It seems possible that the need to
keep track of such allocations and transactions was enough to stimulate
development of a recording system….
The recording system which satisfied these needs, one where specific clay
tokens represented quantities, was very stable. It spread thoughout the region
of western Asia and remained current there for four thousand years. The
second major step followed another cultural landmark, the emergence of
cities….[14]
The development of an urban economy, rooted in trade, must have multiplied the
demands on the traditional recording system. Not only production, but also
inventories, shipments and wage payments had to be noted, and merchants needed
to preserve records of their transaction….”
The Replacement of Tokens by Symbols|
Most significant seems to have been the development of token-based
contracts. These contracts are represented now by clay envelopes, usually
sealed with the marks of two merchants, hardened by baking, and containing
within them the numeric tokens representing the amount of goods exchanged.
Such a contract in hand, a middle-man could transport goods from one city to
another with a guarantee to all that neither the shipment nor the terms had
been altered. But, since the contract was validated by remaining unopened, one
could not tell what it said without destroying it; consequently, it became
customary to impress on the outside of the envelope the shapes of the tokens
contained inside. The tokens were pressed into the clay envelope with a
mnemonic intention based on one-to-one correspondence; the marks they made came
to represent the contents of the envelope. The external markings were not
invented to replace the tokens sealed within the clay envelopes, but that is
what, in fact, happened. And this replacement of tokens, signs of things, by
symbols — the impressions they made in a soft clay surface — was the
beginning of writing.
The Flowering of Effects — from Adaptive Development
According to this scenario, writing was not invented to transmit ideas;
but in the history of the west it has been a most powerful force in doing that,
the primary means by which man has been able to extend communication beyond the
circle of his immediate acquaintance, both in space and time. The functional
lability of written symbols permitted a flowering of effects to derive from the
adaptive development of writing’s precursor, an accounting function, in
response to a sequence of specific needs.
I see in this cultural example, and in Jacob’s vision of evolution [15]
the same processes of bricolage whereby an active agent applies pre-existing
resources to new problems — through which process he defines what is novel in
the problem and extends by modification his earlier resources. Occasionally
these newly modified resources have a far wider application than their
precursors. Such functional lability, developed through application to
particular problems, is the root of creativity in evolution, culture, and
personal development.
We can bring this broad ranging claim down to earth in the case of cognitive
development by trying to penetrate more deeply into the Piagetian notions of
assimilation and accommodation.
Bricolage as Problem Deformation: C. S. Peirce and Abduction
People frequently confuse “abstract” with “generally applicable”. What
one DOES could apply generally and merely seem abstract if problems in the
external world are deformed to fit processing by highly particular structures
of the individual mind. Piaget named such a process of problem deformation
“assimilation,” taking that name at various times both from an alimentary
metaphor and processes of linguistic change.
If we move in the direction of more logical descriptions, the most apt way to
characterize such a mind’s logic in action is as proceeding less by deductive
or inductive logics than by what C.S.Peirce named “abduction” [16].
[Abductive inference] …is where we find some very curious circumstance, which
would be explained by the supposition that it was a case of a certain general
rule, and thereupon adopt that supposition.
Peirce’s theory of types of inference: simple examples
DEDUCTIVE INFERENCE
the rule: All the beans are from this bag are white.
the case: These beans are from this bag.
IMPLIED result: These beans are white.INDUCTIVE INFERENCE
the case: These beans are from this bag.
the result: These beans are white.
IMPLIED rule: All the beans are from this bag are white.ABDUCTIVE INFERENCE
the rule: All the beans are from this bag are white.
the result: These beans are white.
IMPLIED case: These beans are from this bag.
Peirce’s terms rule, result, and case translate into a more concrete vision of
the evolving mind as follows. The “rule” becomes a cognitive structure, a
model of a situation, what is known in the mind. The “result” is the problem
situation actually confronted. It presents immediate data such as “these beans
are white.” The implied case is the interpretation of the problem through the
model.
Abduction is prior to Deduction and Induction
Abduction is prior to deduction and induction. This formulation
emphasizes that a primary aspect of problem solving is the adopting of a
hypothesis about “what’s what.” The perspective from which you view a
situation determines what problem you imagine you are attempting to solve. This
is so less by choice than by necessity: one can recognize the unfamiliar only
by first misapprehending it as something familiar, then progressively
distinguishing it from things actually familiar in the past. Thus, the core of
abductive inference in human problem solving is the deformation of problems to
fit the recognizing processes of models in the mind.
The best computational embodiment of such a view of mind is presented in
Sussmann’s HACKER system (Sussman, 1975), wherein a mental “programmer”
perfects old programs and assembles new ones with the guidance of failure
information from its previous mis-appreciations of presented problems.
Similarly, the Merlin system (Moore and Newell, 1973) matches a target/goal
description against stored descriptions by some higher-level process making
terms variable until partial equivalence is achieved at some level of
variation. In contrast, the essential element of my vision of the evolving mind
is that a number of active descriptions apply themselves simultaneously, each
performing its best match/deformation, and those with sufficiently good match
to the specific problem go forward while other competitors infer nonsense and
inapplicable results. It is the difficulty of applying generated conclusions
that defeats the parallel effort of the less successful competitors.
Convergence
With such a vision of mind, it is possible to understand how generally
applicable skills arise from the coordination of diverse structures based upon
particular experiences with processes that are more like abduction than
generalization [17].
Bricolage, as a name representing the functional lability of cognitive
structures, with its focus on the interaction of pre-existing tools and
available materials, helps to explain the power of the particular in
determining the course of development. Here is a profound convergence,
permitting a unification of points of view through which the form of evolution
of species, the rise of civilization, and the pattern of development of the
individual mind can be seen as the parallel results of the same sorts of
historically determinate processes.
Bricolage and Cognitive Structures
What are the practical advantages of discussing human activity as
bricolage in contrast to goal driven planning? The first advantage is that it
is more natural, a more fit description of everyday activity than planning is.
The second is that it is more nearly compatible with a view of the mind as a
process controlled by contention of multiple objectives for resources than is
planning, which seems to call for a single center of decision or a chain of
decisions in a pre-ordered form. The final and most important advantage
permits a new vision of the process of learning. Bricolage can provide us with
an image for the process of the mind under self-construction in these specific
respects:
-
– if the resources of the individual’s mind are viewed as being like the tools
and materials of the bricoleur, one can appreciate immediately how they
constrain our undertaking and accomplishing any activity. -
– not only constraint comes from this set of limited resources; also comes
productivity, the creation of new things — perhaps not exactly suited to the
situation but of genuine novelty. -
– the mind, if seen as self-constructed through bricolage, presents a clear
image of the uniqueness of every person: -
* each will have developed his own history of conceptions and appreciations of
situations through which to make sense of the world. -
* each will have his personal “bag of tricks,” knowledge and procedures useful
in his past. -
* each will have his own set of different, alternative objectives to take up as
chance puts the means at his disposal.
If viewed as claims, such statements are not easy to prove. However, they
provide a framework for investigating learning which could be valuable by NOT
demeaning human nature through assuming it is more simple than we know to be
the case. With such an intention, it is reasonable to ask if these ideas can
be applied to a specimen of behavior — one able to sustain extended analysis
— so that we may return with a richer and more precise application of how the
development of objectives and learning create the self-constructed mind.
Implications for Method
The image of bricolage, when extended from a description of behavior to
a characterization of typical human thought, suggests how to explore human
behavior for evidence about mind. It gives hints of what to look for in the
search for the psychologically real (concrete experiences and their sequelae).
It emphasizes the importance of following an individual’s selection of
activities and the need for sensitivity to cultural pressions in tracing the
development of mind on a Piagetian scale of development. Given that such
observation has provided a fecund method to study the development of
objectives, should it not be extensible for the exploration of such issues as
how the fragmentary character of experience affects the mind and how
significant learning happens in concrete situations? After this analysis of
Robby’s project, such questions generated The Intimate Study.
Publication notes:
- Written in Autumn 1976. Augmented and rewritten in 1984.
- Published locally as a Logo Working Paper in February, 1977
- Re-Published in this form as the first analytical chapter of “Computer Experience and cognitive Development.” John Wiley, 1985.
Text notes:
- In precise use, the word “goals” generally implies struggle and hardship in achieving some end; the contrasting word “objective” implies the attainability of the end. These and other contrasts are laid out in extensive detail in Webster’s Synonomy.
- The character, development, and interaction of such microviews is explored through the empirically based analyses of Computer Experience and Cognitive Development (CECD). A compact overview is presented in chapter 7 of that work.
- There is a major issue here, the validity of induction, which like a hidden shoal I would prefer to avoid. Note in the appendices of CECD the extended citation “Goodman: On rightness of rendering” his reference to frantic attempts to justify the process of induction. Prefer, if you can, his more balanced view.
- What this might mean in practical terms and how one might gather evidence for or against such a conjecture are central issues dealt with in Chapters 2 through 5 of CECD.
- If one pushed a vision of the child as scientist, one might want to argue that he is “testing an hypothesis” about the application of his theory to a particular case. A slightly weaker position is that the child is exploring the range of application of his procedure. This is still “scientific” in the sense of many physical laws, such as Hooke’s Law of elasticity, which are valid only over the range of circumstances to which they are found to apply. More importantly, this view emphasizes the abductive rather than inductive character of the inferences involved. See, however, my final character of Miriam italicized at the end of “A cognitive profile” in the appendix (p. 221 of CECD).
- A short technical note. The procedures invoked here, BOX and TRI, were written to take inputs as lists and implement default values for variables not specified; consequently, their syntax is quite non-standard.
- This is a central theme of CECD; its more precise exposition and its role in learning appear more explicitly in chapters 2 and 4 of that book where it is discussed as the elevation of control. See also in CECD the extended citation “Papert: On the elevation of control.”
- Pp. 17, 21 in The Savage Mind, University of Chicago Press, 1966.
- A research program and an assemblage of ideas while I was their colleague, the society of mind theory represents the intellectual backdrop against which my work may be seen as the major empirical investigation of learning developed in that MIT community during the late 1970’s. Minsky continues his effort to produce a work which will make these ideas generally accessible as a theory.
- An example bearing on this contention is the program AM which has succeeded in inventing the idea of number. The program is described in the thesis by Douglas Lenat, “AM: an Artificial Intelligence Approach to Discovery in Mathematics as Hueristic Search.” For a perspicuous analysis of the successes of that program, see “Why AM and Eurisko Seemed to Work,” by Lenat and Brown (1983 AAAI conference).
- My version is based on the article “How Did Vertebrates Take to the Air?” by Roger Lewin in the Research News section of Science (July 1, 1983). The original by Caple, Balda, and Willis appeared in the American Naturalist (121, 455 (1983)).
- Lift is the common name for the Bernoulli effect, the pressure differential created by airflow around an asymetrical convex object. If such an object, an airfoil, is flat on the bottom and curved on the top, it will experience net pressure up.
- This citation and general view is derived from “The Earliest Precursors of Writing” by Denise Schmandt-Besserat in Scientific American, June 1978.
- Schmandt-Besserat, op.cit.
- See the extended citation at p. 253 in CECD “Jacob: On Bricolage in Evolution.”
- Peirce, the major American philosopher of the nineteenth century, wrote popular articles as well as more technical work. His most accessible work, well represented by the essay “The Fixation of Belief” is both profound and charming. The idea of abduction sketched below was introduced in his essay “Deduction, Induction, and Hypothesis.” A technical analysis of his developing ideas of logical fundamentals may be found in Peirce’s Theory of Abduction by K. T. Fann.
- Chapters 2 and 4 of CECD show extensive, detailed examples of how such ideas can be applied in describing a specific mind and its development.
