COGNITIVE ORGANIZATION
The explanatory dimension of cognitive organization is the path of genetic descent of specific cognitive structures. Were it possible to represent both sensori-motor schemata and late developed structures explicitly and completely, tracing in detail the descent of the latter from the former and identifying the timing and context of ascribable structural changes would be the ideal method to probe the character, the contingencies, and the causes of natural learning. Even some local success at tracing cognitive structures to their immediate antecedents in experience and in the mind, as has been achieved in previous chapters, is worthwhile. But what is really needed is a more ambitious attempt to specify how local clusters of cognitive structures interconnect among themselves and with their most fundamental antecedents in development. The preceding studies have not asked why, in principle, some links occur between late developing structures and others do not. To deal with such a problem is the purpose of this chapter.
The Main Idea
The central proposal is to discriminate among the major components of the sensori-motor system and their cognitive descendents, even while assuming the preeminence of that system as the basis of mind. Imagine the entire sensori-motor system of the body as made up of a few large, related, but distinct sub-systems, each characterized by the special states and motions of the major body parts, thus:
| BODY PARTS SUB-SYSTEM |
SENSORI-MOTOR | MAJOR OPERATIONS |
| TRUNK | SOMATIC | BEING HERE |
| LEGS | LOCOMOTIVE | MOVING FROM HERE TO THERE |
| HEAD-EYES | CAPITAL-VISUAL | LOOKING AT THAT THERE |
| ARMS-HANDS | MANIPULATIVE | CHANGING THAT THERE |
| TONGUE, ETC. | LINGUISTIC | SAYING WHATEVER |
Granting the distinctness of these five major sensori-motor sub-systems, notice that much of the activity of early infancy specifically involves developing coordinations between them: between hand and eye, between legs and body, between the sound expression system and what is felt, seen, or desired. If the sensori-motor system is fundamental in the development of the mind, one might assume that any significant structure at its base — such as the body-parts model here — should ramify through all descendent cognitive structures developed from interacting with the experiences of later life. I apply this assumption in the following analyses and interpretations of material from this empirical study. The objective of this analysis is ascribing cognitive structures over time and tracing the filiations of those ascribed structures and the interactions of those filiations as a developing cognitive organization.
What are the Parts and How do They Relate to Each Other ?
The discussion of “organization” requires that one describe things that are disparate from one another and then specify how these different things are related. The body-parts mind proposal serves the function here of separating groups of cognitive structures on a large scale. Thus I will argue that some cognitive structures are descended from ancestors in the locomotive sub-system and others from ancestors in the visual sub-system. There remains then the question of the extent to which such structures become related to each other and under what circumstances.
If there is body-based disparateness, what it there that ever leads to subsequent integration? Most importantly, and obviously, the achievement of functional goals requires the cooperation of disparate cognitive structures and subsystems of such structures, e.g. crawling to get some desired object requires the use of arms and legs. Thus the progressive organization of disparate structures and subsystems proceeds from the needs of the individual as a complete being. In this study of a child’s encounters with geometry, because she had no pressing need to integrate her knowledge, we may hope to see in slow motion the disparateness of knowledge and the processes of its integration more clearly than we would in domains where one might be more directly driven to unification.
The body-parts mind proposal is an obvious one but not a common one. Most scientists follow that sort of uniformitarian commitment witnessed so clearly in the formulations of Piaget or Newell and Simon. Those who do concern themselves with the synchronic organization of mind – and thus follow a “divide and relate” strategy – usually focus on sensory-dominated divisions of mind. (The work of Hunt, 1973, is an example.) Focussing as it does on the descent of cognitive structures from ancestors in the motor subsystems, the body-parts mind proposal is implicitly committed to favoring the activity of the subject in the creation of cognitive structures over the impression of sensations on the mind. In this specific sense, the proposal shows the influence of Piaget.
Against the Assumption of Uniformity
Even if the mind is a network of information structures comprised of the same types of elements, one need not conclude that it is uniform. Microviews are shaped both by their specific descent from body-defined sub-systems and by their interconnection possibilities in terms of those sub-systems. That is, one may see a square and recognize similarity in moving through the pattern of a square, but it would be an unusual mind that asked “what is the sound of a square ?” In sum, the connections between late-developed cognitive structures mirror — and are guided by — the interconnection possibilities of the sensori-motor system which are first explored and described in the motor programs developed during the sensori-motor period of infancy.
This idea, which I name the “channelled description conjecture,” is not an hypothesis which was posed for experimental confirmation; rather, it is a ground of explanation which I find useful in making sense of knowledge Miriam developed and failed to develop during her many encounters with “geometry” during The Intimate Study. Any critical reader will note my interpretations can not be coercive; the evidence is just not good enough. The arguments here must be seen then as explorations in considerable detail of how a distributed model of the sensori-motor system can help in understanding the developmental path of a mind. Because the idea I present here as the body-parts mind is focussed on the individual body and is entirely asocial, it can at best help us understand some significant part of cognitive development[note 1].
The Domain
In preceding chapters, I described the development of interrelations among Miriam’s microviews of common ancestry. Here we are confronted with how to understand the genesis of relations among microviews of arguably different lines of descent. The working out of this process, in detail, is the burden of the following analysis and interpretation of Miriam’s learning about essentially different kinds of geometries (“essentially different” in that they connect naturally to different kinesthetic sub-systems).
My application of the term “geometry” to our work, as much as that work was very limited in scope, is justified by Miriam’s having dealt with the primitive space descriptions of turtle geometry and coordinate geometry. In turtle geometry, the primitive terms of description are actions, that is, executed commands to move forward or back some distance or to turn right or left through some angle. The commands are implicitly directed to an agent, the turtle, and are state centered, i.e. go forward so far from wherever-you-are and turn right so much from wherever-you-are-heading. These are the basic geometric concepts Miriam was to deal with during our project. In coordinate geometry, any point in a plane is represented as an ordered pair of numbers which measure distance along a perpendicular set of axes. Miriam’s use of coordinates involved specifying that some object should appear at a destination described by this ordered pair of numbers.
Designs versus Navigation
One of the practical challenges of turtle geometry is the child’s achieving a bridge between the world of mathematical design on a video display and the everyday world of going forward and turning right, “navigation” if you will. In the world of body geometry, a right turn would be well served by anything between 80 and 100 degrees. In designs, the difference one degree makes may be profound. Such a difference in quantification sensitivity suggests that the experience of these phenomena must result in disparate structures in the mind.
Further, how different for a child must appear an “angle” when it is first, how much a person turns and second, an abstract number on which some incomprehensible computer procedure operates to create a mysterious product. Although the labelling of our language, an implicit form of instruction, promises connection between disparate realms of ideas, it must be through the individual’s experience and intellectual labor that bridges between these disparate realms are constructed.
For the two task domains of child or turtle navigation through space and computer-generated design, the ultimate relation is through iteration. In the later section “Computer Generated Designs,” I follow Miriam’s progress toward understanding such a relation. Tracing the development of a bridge between the microviews of navigating in turtle geometry and creating computer-generated designs is the concrete problem through which I pursue the central theme, the developing organization of disparate cognitive structures.
TWO GEOMETRIES
Over many years at the MIT Logo Project, I have seen that turtle geometry is easily accessible to many children, even pre-schoolers, when introduced with the mechanical “floor turtle.”
This access derives from the connectibility of knowledge about the turtle’s actions to the child’s own personal geometry, that egocentric knowledge of space we all develop in our earliest years. Turtle geometry is so natural in this specific sense that it is somewhat perplexing to define what a child learns from experience with it. One could almost claim that even an infant knows turtle geometry in a practical form. I have seen a baby at six months turn on her belly to reach a toy initially beyond her grasp and at seven months crawl forward to reach another toy. The states before and after her action were obviously meaningful to the infant and their changes were effected by intended actions. These states of the infant’s geometry are specifiable either by naming, (“I am here and the toy is there”), or by operations, (“if I turn this much and go that far I will get from here to there”). The origin of the geometry is progressive; it resides at the body and moves with it. It would be absurd to argue that Miriam didn’t learn such things until she was six.
What Does It Mean to Learn Something Natural ?
To approach the question of what it means to learn something which is natural, one needs a very specific way of describing how new knowledge relates to old knowledge and what constitutes a significant difference between one state of knowledge and another. Let me play the Devil’s Advocate: the child’s actions and the operations of turtle geometry are sufficiently congruent that those operations are not learned in early encounters with turtle geometry; all that can be said to be learned is the application of those actions to new domain — the floor plane of the mechanical turtle or the video display domain. Couched in such terms, this conclusion demeans the importance of applying knowledge. It is especially misleading if, as I believe, knowledge is augmented and refined primarily through the application of old knowledge to new problems for which it is not yet perfectly suited.
Turtle Geometry
What is novel in the turtle geometry context is the persistent, explicit quantification of actions. I now pursue in detail the growth of Miriam’s knowledge about angles, and even more specifically, about turning 90 degrees, since this limited topic provides the clearest example of how her prior knowledge connected with quantification in turtle geometry.
Does a child think of turning as a stepped action or as a continuous one, such as the turning of a wheel around its axle or of a clock’s hands ? Miriam did not conceive of turning as continuous. If turning is a stepped action, quantification reduces primarily to problems of scale. What is a good default number to try when you can make no well-motivated guess about what’s appropriate ? What is the smallest increment that makes an interesting change ? Miriam appears to have recalled from experience with turtle geometry several months earlier that you need big numbers as operands to generate significant actions. During a review session (age 6;0;23) where she played with SHOOT, a game of locating the video cursor in a circular target, her first angle operand was fifty degrees, and she repeated her “right 50” three times till the turtle was nearly pointed at a target. Her first distance was 20 turtle steps. It was increased by increments of 10 for successive trials in shooting the target.
In Logo Session 3 (age 6;0;28), Miriam revealed the limits to the connectedness of her thinking about turtle geometry and her personal geometry while “playing turtle,” that is, simulating with her own body the responses of the robot turtle to Logo commands:
| Bob: | There’s another way we could play SHOOT, if we didn’t want to use the computer; I made this hoop ( a three foot diameter plastic circle). We could play SHOOT (dropping the hoop onto the floor). |
| Miriam: | You direct me how far to go and then I’ll do it. |
| Robby: | (Assuming control) Right 90. |
| Bob: | (to Miriam) Right 90…. Do you know what to do ? |
| Miriam: | Yeah (She turns right a little, about 30 degrees, counts 1,and continues counting one for every 30 degree turn up to 15; that is, more than one full turn.) |
| Robby: | (laughing) |
| Bob: | We’ve got a bug here, don’t we. |
| Miriam: | (continues and counts) 24, 25, 26, 27…(laughing, she continues) 30, 31, 32, 33, 34, 35, 36 — |
| Bob: | (interrupting) STOP ! We’ve got a turning bug of some kind here. What does it mean when we say “RIGHT” then a number ? |
| Miriam: | I’m the turtle, see. You go right, this. (Again turning right about 30 degrees.) |
| Robby: | Suppose I told you “left 90.” You do THAT. (Robby demonstrates.) |
| Miriam: | O.K. |
| Bob: | What was that, again, Rob ? |
| Miriam: | If you’re facing like this, he said turn like that. (Miriam lifts her arm at her side, then “jumps” her feet around under it.) |
Because Miriam had no strong theory of how “90,” the operand of Robby’s command, was to be interpreted, in her simulation of the turtle she fell back on the personal geometry’s interpretation of what “right 90” might mean, that is, turn to the right a little bit, 90 times. Such is a sensible and sound tactic. By an accident of history, however, the degree-numbers of the Babylonian scale by which we commonly quantify turning do not fit transparently with the terms of turning in personal geometry, that is, right or left (90), halfway (180), and all the way (360).
Playing Turtle
Playing turtle is not merely a form of instruction by adults within the Logo community. As Robby showed above, it is also a child-accessible form of explanation. Robby and Miriam simulated the game SHOOT, usually played on the vertical video-display screen, with their body motions in the horizontal plane[note 1]. To communicate an idea of quantification, the most effective instruction was, in this case, a body-based simulation of what the number meant in the domain. This kind of observation is one that should be recognized as telling us how important to a child’s cognitive development is relating current problems to past experiences.
Navigating the Display Turtle
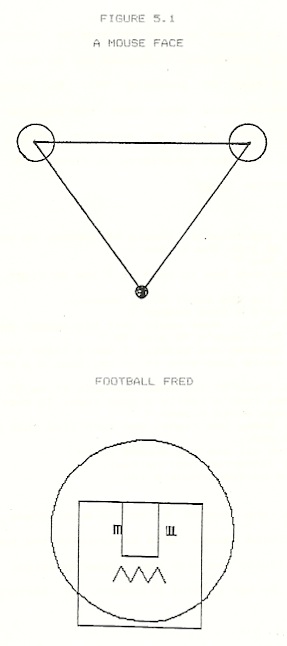
In two subsequent sessions, Miriam came to appreciate and verify the correspondences of the degree scale and her personal geometry. In Logo Session 6 (age 6;1;3), we worked through a short series of speculations about how turns of 90 degree multiples affect the turtle’s heading. Typically, Miriam attempted to recall the number value of an earlier observed heading while Robby attempted to deduce the result from remembered turning actions. Her method exhibited the fixed frame of reference in which she saw 180 as related to heading more than to turning. A few days later (in Logo Session 9 [age 6;1;9]) Miriam made the explicit connection between 90 degree multiples and turning around. She was making a simple picture of a mouse face (see Figure 5.1). The head was an equilateral triangle with circular ears and a small blob for a nose. Miriam assembled these components in the sequence suggested by Ed Emberley’s book “Animal Faces”.
Miriam planned to draw the head by invoking TRI[note 1]. After she cleared the screen, I advised her to turn the turtle before drawing the head by invoking TRI. My candidate turn was 60 degrees, which would have been the smallest turn leading to a horizontal side above an opposite vertex, the nose. This projection of mine interfered at first with my understanding Miriam’s better idea:
| Bob: | If the triangle should be turned, we should sort of turn the turtle — |
| Miriam: | How ? |
| Bob: | You know how to turn it ? You go right or left turn. |
| Miriam: | (as she keys) R, T, space… |
| Bob: | What’s a good number ? |
| Miriam: | 70…. What would that big number be ? 90 plus 90 ? What’s 90 plus 90 ? |
| Bob: | A hundred and eighty. I don’t think that — that would just make it — oh, that’s a brilliant idea ! |
| Miriam: | (Keys RT 100 then corrects it to RT 180) |
| Bob: | Gee, that’s really a good idea. Is that what you knew would happen ? |
| Miriam: | Robby was right. One turn like that would be 90 and… |
| Bob: | Then all the way around is — |
| Miriam: | (Interrupting) Halfway. |
| Bob: | And halfway round’s 180. |
When once she caught on to the specialness of 90 and 180 degrees, Miriam became able to navigate the turtle in its space quite skillfully and with good comprehension. This is later witnessed by her careful placement of features in “Football Fred” (see Figure 5.1) and other drawings. From Miriam’s explicitly witnessing Robby’s correctness, we may infer she was following his implicit advice to interpret what she saw on the video terminal in terms of her personal geometry.
Coordinate Geometry: Robby using R.A.F.
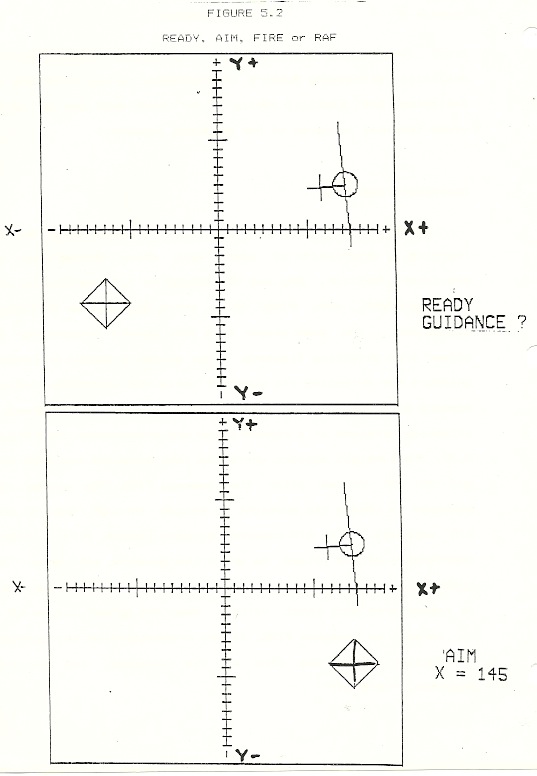
Getting around in a system of absolute coordinates requires learning a description of space with which Miriam was not previously familiar. She was introduced to X,Y coordinates with the game READY, AIM, FIRE (RAF), which was written at Robby’s suggestion.
The game player is a tail gunner protecting his bomber from attacking fighters. The gunner’s canopy provides a gridwork for orienting his gunsight while the attacking airplane appears in a second, remote space. The command READY draws an attacking airplane at a random locus and orientation (see Figure 5.2). The gunsight appears where the last airplane was shot down and is not re-set after the command FIRE. The gunner now attempts to locate his gunsight on target through one or more AIM commands. The AIM command requests inputs, first X then Y coordinates of the place to which the gunsight will move. The gunsight moves horizontally or vertically from its former locus in response to each input value. When the gunner judges he is on target, he commands FIRE. If the cross-hairs of the gunsight are located within the area of the fuselage, the airplane explodes, “KA-BOOM!”
Robby showed an immediate, easy grasp of the game; it was not itself inaccessible. His engagement was intense and his understanding sound, as is shown by his immediate and spontaneous retro-fitting of this new space description onto the familiar problems of his SHOOT experiences when first introduced to R.A.F.:
| Bob: | (with the airplane and gunsight on the screen) This is X, along this way. If it’s over here, those are numbers of X greater than zero. If you’re over here (on the left), it’s numbers of X smaller than zero. |
| Robby: | Hey, Dad. You know what I would do if we were playing SHOOT ? I’d say “SHOOT X 120” so it would be even with the target, then “RIGHT TURN 90, SHOOT Y” so it would go in. |
| Bob: | I don’t understand. |
| Robby: | What I would do is get him lined up with the target, then right or left turn it, then I’d say SHOOT the other number to get it in because of the X’s and Y’s and get it in[note 1]. |
A reasonable translation of Robby’s excited expression would be this: I would move the turtle along the x-axis until I got it lined up with the target then I would turn it vertical and shoot in it (determining the distance by reading it off the scales of the y-axis).
Robby’s easy comprehension of this task domain renders the process of his learning impossible to study. In contrast, Miriam’s painful struggle with coordinate geometry is more open to examination.
Coordinate Geometry: Miriam using R.A.F.
The two children were introduced to R.A.F. together (Logo Session 11, age 6;1;12). My objective was to find out how easily Miriam could understand the space description of coordinate geometry. The best evidence is the extent to which she was capable or not of taking advice. My consistent direction was that Miriam should think of the X,Y couple as a name and that all points on the screen had a first and last name, just as she did. Miriam’s initial conception was not conformable to my advice, and between us we generated the confusion cited here from Logo Session 12 (age 6;1;15):
| Bob: | You had Y as minus 60. Maybe you want to make it — |
| Miriam: | (keys a positive number) |
| Bob: | No. Minus. |
| Miriam: | That will make it go up ?… Rubout, minus. Minus…. (keying. As the gunsight rises from Y = -60 to Y = -11)… Minus goes up. |
What this witnesses is Miriam’s partitioning of input values focussed on state change, with the QUANTITY assigned to HOW FAR the gunsight should move and the SIGN determining the DIRECTION of movement; X = -10 means move left ten units. This is an error with respect to how R.A.F. works. Session 14 (6;1;17) marked the end of our early use of READY, AIM, FIRE. My conclusion from these sessions was that Miriam’s focus on two objects, the gunsight and the target, reinforced the disposition she had (from her recent play with SHOOT and other turtle geometry sources) to conceive of the task in terms of differences and state changes produced by corresponding actions. I resolved to make a game of XY values which would not promote this specific confusion.
AN INTERVENTION.
Miriam had long enjoyed making pictures by connecting serially numbered dots in “dot-to-dot” drawings when I introduced her to MAKEDOTS in Logo Session 50 (age 6;4;7). This very simple system executes through two subprocedures, MAKEDOTS and DODOTS. The first procedures requests X and Y coordinates; when both are input, a small square is drawn at the point they define and the location is entered in a list of places. During execution of this procedure the turtle is hidden. Nothing moves anywhere. DODOTS draws lines from the locus of each member in the place list to the next one. Miriam enjoyed playing with MAKEDOTS. The typical execution of the procedures saw alternately our making dots with my interjecting requests that Miriam speculate about where each would appear. The following from Logo Session 54 (age 6;4;13) is typical. It also shows her making an experiment and linking domains of positive and negative numbers at the origin.
| Bob: | I’m gonna make X zero. And I’m gonna make Y zero. Where’s it gonna go ? |
| Miriam: | (with no hesitation) Middle. |
| Bob: | (keying) Absolutely right. |
| Miriam: | I’m gonna make…ah…minus zero and minus zero. |
| Bob: | Where’s it gonna go ? |
| Miriam: | (keying new line) |
| Bob: | Same place. Hah! I guess plus and minus zero are just the same. |
| Miriam: | O.K. |
Catching On: Three Confusions
In the same session as the work cited above (Logo Session 54, age 6;4;13), Miriam rapidly “caught on” to the significance of numbers in the absolute coordinate description of space. What Miriam learned and the genetic path of her learning can be seen clearly in citations from three executions of an RAF variant (with the airplane replaced by an aircraft carrier to be bombed).
The three confusions Miriam grappled with in the following are:
– not relating consistently the X symbol for quantity to the horizontal axis and the Y to the vertical axis on the display screen;
– conceiving the X and Y quantities as state changers and not as partial point names;
– confusing which segments of the axes plus and minus numbers apply to.
These confusions all appear early in Logo Session 54.
Confusions: Detail from Logo Session 54
After she succeeded in bombing her first target at (120, -120), a second target appeared in the third quadrant, approximately at (-120, -120). This quirk of the random number generator, producing two sets of coordinates identical in magnitude, simplified the understanding of how selected inputs produce results. To aim the gunsight at the new target, X had to be changed from +120 to -120. Let us trace in detail Miriam’s solving this problem, since it represents a breakthrough in her use of X,Y coordinates. In the following dialog, focus your attention in the following dialogue on two points: first, how does Miriam keep the gunsight where it is, despite being required to enter an input variable; second, how does she adjust the value (X = -100) to get the gunsight over the target at (X = -120):
| Miriam: | Wasn’t a hundred twenty, a hundred twenty a good idea ? |
| Bob: | Yes. That was very good when the carrier was here (at prior location), but now the carrier is in a different place (pointing to the X-axis). These are minus numbers on this side, and that’s a hundred (a large scale marking). |
| Miriam: | Think I’ll go minus a hundred. |
| Bob: | (pointing to the 100 marker) But that will get it where the big line is. Is that where you want it ? |
| Miriam: | Yeah. (Miriam assumes the gunsight will go onto the X axis where I had pointed) And then what I’ll do is get it down. (Keys X = -100; the gunsight moves over) |
| Bob: | Oh boy. If you can keep the Y just where it is, you’ll be in great shape. |
| Miriam: | Y zero ? |
| Bob: | No. Y was what ? It was minus…a hundred twenty. |
| Miriam: | Yeah. (keys -120) A hundred twenty. (No movement) |
Here Miriam’s first idea was that what she keyed was a state-change operand. When I prevented her from using Y=0, she accepted my specific direction Y=-120. We now continue in this same dialogue to a critical juncture.
| Bob: | All you have to do is get your X over here to the center of the carrier. |
| Miriam: | (Keys AIM and enter) Here I go. X will be… |
| Bob: | Plus or minus ? |
| Miriam: | Plus ? No, minus. Minus 20. (Keys -20; the gunsight moves right — the “wrong” way to [-20, -120].)… Oh grumble. |
| Bob: | Hmmmm. |
| Miriam: | Then I’ll do plus 40 — |
| Bob: | (Interrupting) Hold on. |
| Miriam: | On my next X. |
| Bob: | What you have to understand, Miriam, when you say plus or minus, it doesn’t tell you how much to move the gun, but it tells you the name of the place where it’s going to go. |
| Miriam: | Where ? |
| Bob: | What you have to figure out is what’s the name of that place, where the carrier is. It’s kind of like using MAKEDOTS…. (Points to the carrier) Right now, we’re waiting to put in minus a hundred twenty for Y. |
| Miriam: | Yeah. |
| Bob: | O.K. (Keys it in; the gunsight doesn’t move.) So let’s AIM again, and we know minus one hundred was pretty close (pointing to the marks on the coordinate scale) and this way (left) gets bigger minus. |
| Miriam: | (Puts hands on the X axis to count the division) Minus a hundred twenty (as she drops the line down from the X axis). |
| Bob: | Give it a try. |
| (1)Miriam: | (Keys) Minus 1, 2, 0 (Keys enter; the gunsight moves over the carrier.) |
| Bob: | Right on. If you can keep Y in the same place… |
| Miriam: | A hundred twenty ! |
| Bob: | Plus or minus ? |
| Miriam: | Minus (keys -120 and enter.) |
Miriam’s first suggestion to keep the gunsight fixed was “Y zero.” At that time, she still thought of the Y coordinate as a state-changing quantity. But when that option was blocked, she accepted the previous value of Y [-120] as an alternative. In this second instance, when the X coordinate was so specified as to bring the gunsight over the target, she VOLUNTEERED the correct value for keeping the Y coordinate fixed.
Here is the essential contrast in the simplest case: do you maintain a thing by doing nothing (Y=0, the coordinate seen as a change operand) or by doing what you did before (Y=-120, the coordinate seen as relative to the extrinsic reference point [0,0]). When Miriam tried to modify the X coordinate from -100 to -120, she “naturally” thought of -20 as the appropriate change specification. Her correction, when -20 was proven faulty, was +40, that is, the “compensation” for the error plus what “must” be required to achieve the original objective. Once more the coordinates were seen as change operands. After I told her that “it’s kind of like using MAKEDOTS” and “We know minus 100 was mighty close and this way [left] gets bigger minus,” Miriam for the first time WITHOUT PROMPTING OR CORRECTION got her own solution to a problem in terms of X and Y coordinate values (at (1) above), first locating the gun on the target with X = -120, then keeping it there with Y = -120. I hold that this change of behavior signals an insight, an intellectual breakthough.
Miriam showed at this point two competing interpretations for XY coordinates. The dominant one explained a coordinate value as an operand for change. There were many cases where Miriam’s good success at a target followed my correction of her first candidate, as in the citation above. Did she ever go so far herself as to reject her “natural,” state change interpretation of what coordinates might mean ? She did. This excerpt (from Logo Session 65, age 6;5;6) begins with the gunsight at [150, 50] and the carrier at [100, 100]:
| Miriam: | Over forty, plus forty. |
| Bob: | Is that the name of the place ? |
| Miriam: | (Looking puzzled) |
| Bob: | It’s not how much you’re going to move it. |
| Miriam: | (Looks at the terminal, slapping her forehead) No ! (Putting her hand on the large marker of the X axis) It’s exactly one hundred. So we just say 100. |
| Bob: | You think that’s right ? |
| Miriam: | Yeah. (Keys 100; the gunsight lines up) |
| Bob: | Beautiful. |
| (2)Miriam: | Ahhh….Up. Up 50, but…I mean (moves her finger from the gunsight to the Y axis, then up to the target height; then moving her hand from the target back to the Y axis, holding up her forefinger) One hundred ! (Keys 100; the gunsight moves into the center of the target) Yeah !! |
| Bob: | Oh, I hope you’re gonna get it here. You think so ? |
| Miriam: | (Keys) FIRE. |
| Bob: | (Reading from the display) “Congratulations Ace.” Good for you. |
At (2) above, Miriam spontaneously corrected her first state-change proposal herself, without my intervening.
Discussion
In her introduction to coordinate geometry, three confusions dominated Miriam’s thought. First, she did not consistently identify the X and Y coordinates with their respective axes. This was a superficial confusion. But the second and third are essential confusions in the sense that they derive from and express Miriam’s ability to imagine what the coordinate values might mean.
The second confusion related to interpretation of plus and minus signs as signifying operations which had import for changing the location of the gunsight. When her candidate values did not have expected consequences, Miriam chose to fault the action-sign correspondences she had chosen (these correspondences were clearly, then, an empirical element superadded to a perspective, a “way of looking at things” and deciding “what’s what,” which came from somewhere else). For example, when she keyed -11 for a Y value and the gunsight rose from Y = -60, Miriam concluded “minus goes up.”
The third confusion was identification of the coordinate quantity as a value by which a state variable would be changed. Miriam analyzed a form such a +35 or -60 into two constituents, an operation signifier and and operand signifier (with sign omitted, the quantity was interpreted as having an implicit or default operation specified). She interpreted the quantities as having a structure they do not have. Why ? There are several reasons. A first one would be called a lexical convention. Plus means “add”; minus means “take away”. Both are operations whose operands change the value of the terms to which they apply. A second reason is the task itself. One object, the gunsight, is to be moved over another, airplane or carrier. The salient difference is that they are apart. Action is the way to reduce such a difference, i.e. move the gunsight from here to there.
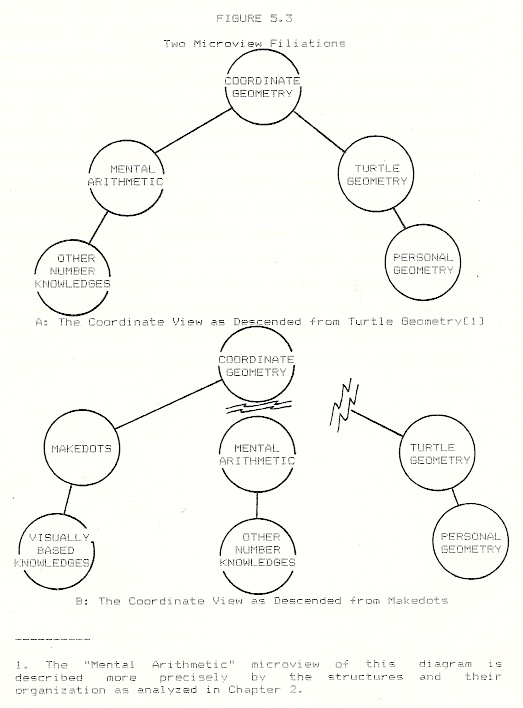
The Descent of Microviews
The microviews of experience which Miriam called on to do turtle geometry and coordinate geometry are sketched in Figure 5.3A (The Coordinate view as Descended from Turtle Geometry). At any locus in such a genetic cluster of microviews, the temporally earlier microviews can be called the ANCESTORS of those developed later. Thus the view of personal geometry is ancestral to turtle geometry. That personal geometry microview, developing from a coordination of the somatic and locomotive sensori-motor subsystems, has those subsystems as its ancestors.
To the extent that number knowledge gave form to Miriam’s (erroneous) conceptions in the Coordinate Geometry microview, that arithmetic knowledge (+ and – themselves as signifiers of state change) indicates non-geometric ancestors. If the Turtle Geometry microview and Arithmetic microviews are considered as separate, one might call them COGNATE microviews.
An Inappropriate Ancestral Microview
Miriam’s basic confusion was to conceive of coordinate geometry as essentially like turtle geometry and arithmetic and that from them she could infer what were the significant operations and the character of elements in that coordinate geometry domain. Miriam assumed such a relation obtained when in fact it did not. That is, her ancestral microviews of arithmetic and turtle geometry were providing, through analogy, strong hypotheses for “what was what” in this new domain. Is it possible she could have thought of the coordinates of Ready Aim Fire as something other than she did? If coordinate geometry is unnatural as turtle geometry is natural, maybe she had, in effect, no choice. How can I make such a statement seem sensible ?
Let me put you in Miriam’s position. Suppose you confront a problem beyond your experience. That system of perspectives (the parsing into part and whole relations) and procedures you need even to comprehend the problem is inchoate. You can only begin to make sense of a more-than-trivial problem if you can see it through the perspective of an ancestral microview, which provides a preliminary parsing of the relevant forms into parts and wholes with which you can attempt to reason. Such ancestral views will also communicate strong hypotheses about what functional procedures might be appropriate for experimental testing. If you lack, in fact, experience which might have provided you with relevant ancestral microviews, what will happen ? Will you not attach your new problem-context-specific microview to an inappropriate cluster of ancestral microviews? Having made such a commitment, Miriam was not able to take advice wherein the forms (+55 or -60) were not analyzable into the constitutents as she saw them, i.e. operation code and operand. She abandoned R.A.F. early in the project.
A Post-Cedent Ancestor
My intention in introducing MAKEDOTS was to provide, although temporally after the fact, an experience that could lead to development of a logically ancestral microview for the Coordinate view. Miriam could not interpret the X and Y coordinates as names when it was possible to interpret them as actions. MAKEDOTS was designed to appear action-free. The only events were the appearing of dots upon their being named.
When playing with R.A.F. in Logo session 54 Miriam’s insight followed hard upon my advice that “It’s kind of like MAKEDOTS.” If we merely note that “analogy” was a significant factor in her insight, we miss the central point. This particular advice was not about some transient similarity; it was advice about how Miriam should organize her mind. It directed her to relate coordinate geometry to an experience which assigned meaning to elements by parsing the forms encountered in a way different from that of turtle geometry and arithmetic. And she was able to take that advice — because she now owned a microview wherein her perspective, in fact, fitted the requirements for R.A.F. That is, MAKEDOTS could serve as ancestral to the Coordinate view though it was temporally a later creation. I name such a microview a POST-CEDENT ANCESTOR. This contrasts with the GENETIC ANCESTOR (in this case the microviews of turtle geometry) to which the new structure originally related (in this case, the coordinate geometry view).
Miriam had trouble in Logo Sessions 54 and 55. She still saw X and Y as having an operation-operand structure, but there was a significant advance. When I intervened to inhibit that view of coordinates, she could now interpret their signification through her perspective on coordinates in MAKEDOTS, i.e. she owned a competing, albeit secondary ancestor to her coordinate geometry view. Miriam’s achieved self-directed inhibition of the coordinate geometry connection to the personal geometry cluster only at the very end of The Intimate Study core period (in Logo Session 65); this is important precisely because it shows how gradually she broke the dominance of the connection between a coordinate geometry microview and the personal geometry cluster.
The MAKEDOTS experience permitted changing the way Miriam saw one small corner of the world. Given the assumption that a change in functions derives from a change in cognitive structures or their organization, this implies that the MAKEDOTS experience created some structure which functioned as a powerful idea for Miriam in the developmental sense. (That is, it played a significant role in respect of organizing her mind, although superficially trivial in itself.)
The Centrality of Post-Cedent Ancestors
I want to emphasize the importance of the idea of a POST-CEDENT ANCESTOR. The vision of learning implicit in Sussman’s work (1975), I paraphrase as “when you encounter something really new, you CAN NOT, NO NEVER, get it right the first time.” The corollary is the observation that the coherence of mind depends entirely on the connection of new experience to old either by the immediate, analogous connection to ancestral structures OR through the intervention of a POST-CEDENT ancestor.
The next important question then is HOW the wrong connections to preceding experience are supplanted by the better comprehension possible through a later, more logically appropriate microview. One alternative is that suppression takes place, the post-cedent ancestor literally inhibits the interaction of the new microview with its genetic ancestors. A second alternative is that the post-cedent ancestor supplants the genetic ancestor through efficient competition with it. This alternative could explain why the dominance occurs gradually. Such could be one situation in cognitive development where the crisp formulation of an idea or the quintessential suitability of a representation exerts a major functional effect on the control structure and consequently the functioning of the mind. My ultimate proposal here is that post-cedent ancestors are the structures through which the reorganization of mind actually takes place.
Where Ancestors Come From – Reflections on Movement and the Eye
If the fundamental law of cognitive development is that nothing comes from nothing (to use a very old formulation), one should ask what are the antecedents of the cognitive structures based on the MAKEDOTS experience. Approaching this question indirectly, I note that it is more or less easy to imagine that turtle geometry experience connects profoundly to body geometry. If we pursue the distributed sensori-motor model of the mind base (the body-parts mind proposal) MAKEDOTS should obviously connect to the visual component. What that could mean, in detail, depends on how one is able to think of the operation of that sub-system.
The eye is popularly considered primarily a sense organ, but its motor activity is equally important in seeing. It is possible to track eye movements and their relation to the scene within the visual field. Noton and Stark (1971a, 1971b) describe such experiments and propose a representation for the movements of the eye. They noted the targets of looking and described the path of eye movement as a series of saccades[note 1].
Saccades are quick movements of the eye by which the gaze is moved from one point to another At the vertices of the path, Noton and Stark assume “features” are detected. Their experimental result is that the path closes and is repeated again and again. This loop of movement and feature detection they name a “feature ring.” They account for much of their experimental eye movement data as the repeated traversing of the ring. They propose that the currently executing feature ring is in part driven by the information contour of the visual field. Further, they argue that the process of image recognition occurs by matching the currently executing feature ring to a similar feature ring, stored in the past.
Consequently, the MAKEDOTS microview — even if it is “obviously” connected to the visual sub-system — may nonetheless be understood as an outgrowth of the sensori-motor system in a serial, motor and feature detection model (in contrast to an image based model). Although I will not attempt to write any programs to describe what Miriam saw in her play with SHOOT, R.A.F., and MAKEDOTS, it must be understood that it should be possible, in principle if not in fact, to do so. Further, let me propose that the state variables and commands of turtle geometry could be a simple specification language for such programs.
This proposal permits a simple observation which goes to the heart of the commonalities and the differences between the locomotive and visual sub-systems. Even if the MOVEMENTS of the eye may be described and represented in terms similar to those which apply to that of the body moving through space, the elements of visually recognizable experience exist as entities at a higher level of aggregation than do the movements of locomotion. That is, feature rings are like possibly complex procedures and they can not be expected to be directly comparable to primitive commands. This simple point suggests that consequently linking together microviews descended from visually-based and locomotive-based sensori-motor components may not be a trivial task. This issue becomes a focal concern of the next section, as we explore Miriam’s experiences in creating computer generated designs.
COMPUTER GENERATED DESIGNS
The basic pattern of the following story is similar to “Two Geometries”: a late occurring experience created a cognitive structure which helped make sense of earlier experiences. In contrast, however, the experiences reported in this section were more various and developed in a fragmentary, overlapping, and much entangled order. The variety of the material and Miriam’s reception of it was considerable. Engagement was balanced otherwheres by rejection, even rebellion. The concreteness of her understanding was in evidence everywhere. Furthermore, many essential elements of these experiences were of a highly particular nature and involved detail no reader could endure. Consequently, for clarity this material will be presented in an order more logical than chronological and descriptions of the experiences themselves will be more summary than thorough[note 1].
The Interconnection of Late Developed Structures
A central difference between this section and “Two Geometries” is in the use made of the diverging aspect of knowledge growing out from the body-parts mind: in “Two Geometries,” the analysis used the case material to exemplify of the separation of microviews descended from different subsystems; here, the interpretations strive to account for the interconnection of late developed structures. The evidence for such interconnection is rare; the character of its manifestation is idiosyncratic and more spontaneous than controllable. Further, even noticing the occurrence of events causing such linkages appears to require both enlisting the subject as a co-observer and considerable good fortune. Difficult to observe because rare and beyond experimental control, like stellar novae, such events are nonetheless suitable topics for scientific consideration, not least because their understanding may be required to appreciate how rare and difficult is the achievement of coherence in the mind.
Ur-concepts of Iteration
The connection mature minds appreciate between the navigation commands of turtle geometry and computer generated designs based on them is through some understanding of iteration — by which I mean here some programmed process for repeatedly executing a sequence of commands with controlled variation. What preceding knowledge, what “ur-concepts” of iteration, did Miriam own ? At least five: incrementing a counting variable; decrementing a counting variable; repetition until stopped by an external constraint; repeating until necessary elements are used up; repeating until a set of objects completed [note 1]. These categories and examples indicate how varied and pervasive are ideas of iteration which a child typically might bring to an encounter with computer procedures.
What we find as this story unfolds is that NONE of these available models of iteration intervened powerfully. Instead, Miriam engaged in activities — both provided by me and spontaneously invented by her — which specifically linked together the microviews derived from her particular experiences.
MPOLY
Miriam’s appreciation of angles, as turning in turtle geometry navigation, has been discussed in “Two Geometries.” Here I focus on a second and very different use of the word “angle” — as the name for a number input a Logo design procedure — which much engaged Miriam early in The Intimate Study. When her closest kindergarden friends joined her individually for an afternoon at the Children’s Learning Lab, they most enjoyed using the computer for making pretty designs.
“…Earlier in the year, Miriam had made paper copies of the image made by a flower procedure and took one for each member of her kindergarden class; the children colored the designs and took them home. While we waited for her flower picture to come out of the printer, Lizzie saw a six-fold, near-triangular multi-polyspiral (see figure 4) which Robby had printed from a different terminal. “Wow ! I want one of those. Show me how to do it.” After I started the MPOLY procedure, Miriam and Lizzie worked together for over two hours creating designs for later coloring. Both girls made some very pretty, novel designs.” (age 6;6;7)
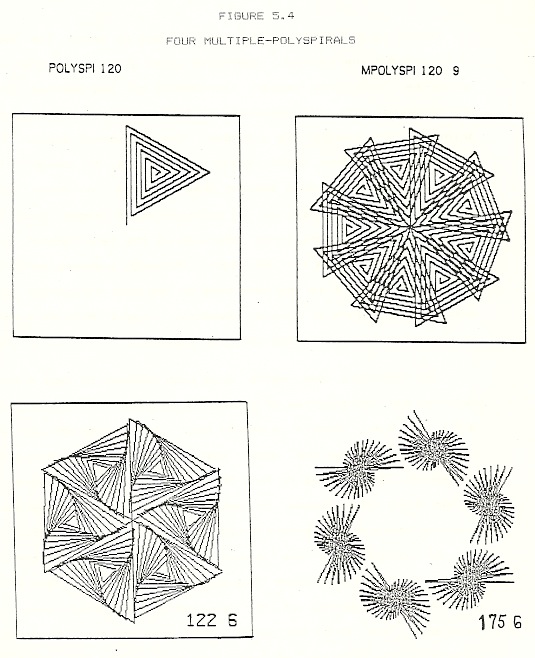
MPOLY is a procedure that makes designs of which the four in Figure 5.4 are typical. Operating under a set of controlling variables (including “angle”) incremented or decremented from the keyboard, with each keyed change MPOLY produces a design and prints on the computer log a number, the polyspiral angle. The children took this angle value as a name by which they identified the individual designs they created in their play with the program. This is an application of “angle” which is only distantly connectible to the use of the term “angle” as a number that tells how far to turn. Although a mature person’s understanding unifies the term used in the both navigation and design applications of turtle geometry, “angle” MUST be a word of multiple meanings to the child or beginner.
Engagement without Understanding
Let Miriam’s own words from Logo Session 23 (age 6;2;2) describe her appreciation of polyspiral designs. On one with an angle of 116, “That’s a beauty one.” When asked why she was incrementing by one the angle value input to a polyspiral procedure, “I’m trying to find the ones I love,” she answered. As the angle value passed through the region of 144 degrees, creating various stella-form designs, Miriam declared, “They’re all my favorites!” The preceding citations do not merely testify that Miriam enjoyed “playing with computers.” They mark part of the quality of her relation to a specific body of knowledge, the MPOLY microview. This view contains knowledge permitting the creation of artifacts both pretty and useful — printed patterns may be colored and given as gifts which, in fact, truly astounded the adults to whom Miriam and Lizzie gave them. Although her comprehension did not penetrate the internal workings of the procedures she manipulated, whatever learning these experiences brought was personally appropriated and not dissociated, in Papert’s sense (1980).
Surprisingly Extensive Particularity
Among the many occasions in which Miriam played with MPOLY, Session 27 (age 6;2;15) is one both playful and fecund, as shown by the following highlights.
After taking my direction a short while, Miriam went her own way. When I suggested she try an angle of 90 degrees, she keyed instead 60. She was delighted to discover the regular hexagonal maze. Miriam then began a somewhat systematic exploration, trying in sequence the angular inputs 70, 80, 90, 100. Next she began varying the angle by one degree — first trying 101, then 59 and 58. After a break in the session, I tried to focus Miriam’s attention on the cyclic symmetry, e.g. the identity of designs made with angles of 30, 390, and 750 degrees, instead of following her lead. Miriam backed away from exploration then but not before she described the design variations near “her” angle of 60 degrees:
| Bob: | (After Miriam had keyed 58) Why don’t you go up by 1 ? Try 59 ? |
| Miriam: | I already did it. |
| Bob: | You did 59 and 60 ? |
| Miriam: | Yeah, 50 and 60. |
| Bob: | Do you remember what 60 looks like ? |
| Miriam: | (A positive head shake) |
| Bob: | What ? Can you tell me ? Can you describe it ? |
| Miriam: | It’s sort of like this (She gestures to the polyspi 58), but bigger, and its got a maze, like in it, but it doesn’t have the curly things (emergent spiral arms). |
Miriam’s MPOLY view at this point was one of fascinating phenomena. The central variable was “angle,” but this angle could not have connected for her in any directly meaningful way with the angle operand of a right turn. Further, the particularity she assigned to angles is staggering to anyone with a more general perspective. How could one imagine “owning” an angle? I infer her MPOLY view saw the micro-domain of computer designs as one of disorderly but engaging objects. Miriam explored this range of phenomena in a regular way. But incrementing by tens did not suggest some sensible way of separating designs, by the numbers, into her later developed taxonomy of mazes, messes, pretty stars, and “ones with the curly things.” We can not consider Miriam’s use of input variables with MPOLY as any different from her use of operands with the primitive operations of turtle geometry. That is, these input variables were no more than numbers given to an uncomprehended (and very powerful) primitive to make it work its attractive but incomprehensible function. The clearest conclusion from these data is that the phenomena of this microworld can be loved and felt as personally owned, even if not at all comprehended in any well-articulated, analytic sense.
Empirical and Analogical Problem Solving
Miriam’s play with MPOLY exemplifies a kind of empirical learning about a small corner of the world. A striking aspect of the knowledge derived from empirical learning is its particularity. In the view of computer designs, Miriam felt she had discovered the angle 60; that the objects it made were hers. Different but similarly particular examples can be found in her views of arithmetic knowledge. She knew the sum “15 cents plus 15 cents equals 30 cents” because the latter was her allowance at six and that for it she could buy two packs of her favorite gum at 15 cents each. Likewise, she claimed to know how to divide, because she knew the specific result that “8 divided by 8 equals 1”.
A second striking aspect of empirical learning is the regular exploration of the space. Thus, in exploring MPOLY Miriam tried in sequence decade-multiples for angle values. Similarly, in an early attempt at multiplication (6;11;13) she tried to determine the product of five and seven by keying in the sequence of commands “5 * 7 =1,” “5 * 7 = 2,” etc. expecting the LOGO error message would change from “you haven’t told me what to do with ‘false’ ” to “you haven’t told me what to do with ‘true’,” thus signaling the correct result when she stumbled across it. This sort of behavior seems like the operation of simple search in a problem space as described by Newell and Simon (1972).
Simple Search versus Problem Deformation
Simple search is not enough to characterize the creativity and complexity of human problem solving. The regular search of empirical exploration should be contrasted with the analogical character of problem deformation, seen in this later attempt to address a multiplication problem (7;7;8):
Miriam was angry with me — and she wrote therefore a five column problem on my chalkboard (1916 and 9232). In a mocking tone, I told her how easy it would be for me to solve. She had her revenge: “It’s not adding — it’s TIMES!” Agreeing that such a problem was difficult, I refused to do it, and she stomped away, leaving the problem undone.
A day or so later, Miriam set out to show me that she could solve that difficult multiplication problem and completed it as below:
1 1
1 9 1 6
x 9 2 3 2
----------
18 8 6 2
What could be clearer than her method in solving this problem ? She substituted multiplication of digits within columns for addition and carried as in addition. In other words, she deformed the uncomprehended problem to fit her existing knowledge, accounting for the problem difference by substituting a new subprocedure within the controling framework of addition.
Simple search can characterize problem solving in task domains which are remote from a person’s past experience. Such domains can be attractive and engaging, as Logo’s turtle designs geometry were for Miriam, but exploration within them tends to be domain-dominated and of an empirical character. In contrast, where interactions and ascriptions of meanings are involved, a complex, pre-existing knowledge structure, a cluster of microviews, is involved. In such cases, problems are assimilated to and deformed by that cluster of microviews. To the extent that intelligence involves integrating the knowledge of a multitude of disparate microviews based on domain-dominated experiences, the most interesting problems and explanations of learning must be based on analyses of experiences which reveal the filiations of structures.
ITERATION: a Lack of Comprehension
Miriam was introduced to iteration as a theme of instruction through the use of a procedure generator. TIMES permitted her to repeat any string of turtle geometry commands as the kernel of an iterative procedure [note 1]. She found it easy to use and wanted to make figures that would “grow” as did those she made with MPOLY. We came to distinguish two different types of growing figures. In the first growth pattern, imperfectly closed figures appeared to precess around their centers, and they grew by turning[note 2]. The second type of growth came through increasing the distance moved forward by the turtle on each forward movement. Miriam wanted to make designs which grew bigger this way, and therefore she needed to know how to use variables.
Three primary means of encoding iterative procedures are step-duplication, looping, and recursive invocation. TIMES produced different forms of procedures depending on the reponse to its question, “Stop on count or data condition ?” The STAR procedure below, one of unbounded tail recursion, was generated by Miriam’s ignoring the request for specification of a stop rule.
TO STAR 1 FORWARD 100 RIGHT 144 2 STAR end TO TRIANGLE 1 IF EQUAL 0 :COUNT STOP 2 MAKE "COUNT (:COUNT - 1) 3 FORWARD 100 RIGHT 120 4 GO 1 end
The TRIANGLE procedure, a decrementing, count-controlled looping procedure, was generated when Miriam’s responded to TIMES’ question with the key word “COUNT.” When such a COUNT variable for the first time, in Logo Session 14 (age 6;1;17), Miriam had little trouble accepting the idea that a quantity submitted to a procedure could specify the number of times subordinate actions were executed (recall RIGHT 90 as “turn right a little bit, 90 times”). By contrast, the role of the variable “:SIDE” input to a recursive procedure “PRETTYSTAR” was not comprehensible to her:
TO PRETTYSTAR :SIDE 1 FORWARD :SIDE RIGHT 146 2 PRETTYSTAR :SIDE + 4 end
Miriam’s failing to discriminate between an iteration controlling variable and one applied as a movement operand value (the distance of a forward command) turned our focus to that task in later sessions.
Little Help from Procedure Analysis
The over-theme of Miriam’s computer experience was that if your want to change or understand a procedure, you must look inside to see how it works, either by execution or analysis. We undertook analyzing procedures in Logo Session 28 (age 6;2;26) to deepen her understanding of variables. I directed Miriam to create a POLY procedure using the fixed count, i.e. step-duplication, option of TIMES with a kernel [FORWARD 200 RIGHT 90 WAIT 30] and a count of 24. TIMES generated a procedure of 24 steps, each of which was [FORWARD 200 RIGHT 90 WAIT 30]. This meant the “kernel” would be repeated 24 times whenever the procedure was executed. Initially, no variables at all were used by the procedure. Miriam read the lines of the procedure, one by one. I stopped her:
| Bob: | What you’re saying is that every time the turtle does something [executes a step] it goes FORWARD 200, RIGHT 90, and waits a little…. How many times does it do that ? |
| Miriam: | 24. (Pointing at the last step) I just looked at that. |
After seeing the execution of POLY and how many times the kernel was duplicated, Miriam still did not know whether POLY required an input variable to control its execution. She tried POLY with no number following and witnessed it working. When she described the object created as “a square” and the activity as “going around,” I proposed we count the iterations to see if the turtle did it twenty-four times. I identified the unit of the turtle’s action as the procedure step, but Miriam identified the unit as the making of a square. When we counted its actions, I counted out loud to “6” – that is, one and a half squares. Miriam continued counting under her breath and concluded with “10. Her count was right in its way: I had counted 6 for six sides; she counted “4” for the remaining eighteen by counting “6” again at eight, “7” at twelve, “8” at sixteen, “9” at twenty, and “10” at twenty four. When I challenged her because I was confused, Miriam made a joke of her response.
I conclude here first that Miriam’s idea of iteration was connected to that of an input value and second that the units Miriam deemed significant were shape-defining more than action-specifying. They applied in terms of repeating visually recognized figures, not of navigating with primitive actions.
Evidence of No Connection Between Navigation and Design
Can one ask for clearer evidence from behavior that Miriam had not connected comprehensibly the views of movement (personal geometry and navigation) with design ? At first I suggested how easy it would be for Miriam (or some other child her age) to understand iteration. Now we have instead an example of how difficult it is to relate a design made from a repeated action to the occurrences of that action. In “Two Geometries,” Miriam could not initially make sense of coordinate geometry because she analyzed that world in terms which were in fact inappropriate. In this case, Miriam saw the thing made primarily as a “square” and not as a shape emerging from the repetition of more primitive actions. She focused on the emergent form, not on the creative actions of the process. We are left with the question of whether her failure to comprehend was an accident of inadequate instruction or a reflection of some deeper disparateness in the mind. (These options are not mutually exclusive.) We will return to this issue and resolve it as best we may after the following survey of Miriam’s later experiences with computer generated designs during The Intimate Study.
The Particularity of Local Knowledge
Miriam failed to understand how the space descriptions of navigation microviews (and in particular the primitives of turtle geometry) related to the figures created by the TIMES generated procedures. That her knowledge relating to various Design view procedures did not connect with navigation microviews meant that the knowledge they embodied retained a “local” flavor. The outstanding characteristic of the local knowledge of isolated microviews is its particularity. What is known is highly circumstantial. This particularity of local knowledge does not imply that the knowledge is insignificant.
Conversely, when circumstances indicate extensive particularity in knowledge we are entitled to infer that the microview itself is created primarily through empirical learning and does not inherit its most important knowledge through descent from an ancestor. The particularity of the TIMES microview is most clearly witnessed in Miriam’s limited grasp of the idea of variables, a central issue followed closely in our work.
Experiences with Variables
Variables are important because of their function, because they permit the use of powerful iterative techniques; understanding iteration presupposes some understanding of variables. When numbers are used, they are used in specific applications. There are five distinct applications of numbers in the Logo language at the introductory level to turtle geometry (procedure line numbers, angles, distances, looping counts, and increments to other values) [note 1]. All but the first of these five uses may appear as variable numbers.
SUMMARY. Miriam encountered these uses of numbers and their uses as variables in the following Logo subsystems. TIMES (described previously) generated various forms of iterative procedures from a kernel of turtle-actions supplied by Miriam. The SLOT system was based on a device — an input terminal which would accept pre-coded cards as commands — designed to render explicit and tangible the sequence of control flow. With that SLOT system, I introduced Miriam to the coding of polyspirals (as in the first design of Figure 5.4) . The SHAPES (polyspiral) programs were a procedural expression of the activities we had pursued with the SLOT system; the procedures applied the value of a quantity DELTA to DISTANCE (the operand of a forward command). In the sessions focussed on FAMILIES of polyspiral designs, I tried to bring to salience for Miriam the issue of the separation and stepping of variables as a powerful idea. Finally, in her experiences with INSPI, she saw the results of applying DELTA to an ANGLE variable. The particularity of local knowledge is most clearly witnessed by examining the detail in specific learning incidents, such as Miriam’s effective introduction to variables through use of the SLOT system.
Variables and the Slot Machine
In an unhappy didactic discussion, I tried to introduce variables generally though liking them to little boxes (representing specific variables with matchboxes) about whose contents one might inquire. For a variety of reasons, Miriam rebelled against this instruction. Her useful introduction to variables was with the Slot machine in Logo session 30 (age 6;2;30). She made some interesting POLY class designs with iterative procedures and fixed quantity instructions, then abandoned the session when I mentioned the word “variables.” Robby in his turn made several POLY designs using both ANGLE and DISTANCE variables. When he finished, Miriam located her “good number” card and decided:
| Miriam: | I want 1, 0, 5. |
| Bob: | Go ahead. |
| Miriam: | How do you do it, the number ? |
| Bob: | First we have to type at the keyboard. |
| Miriam: | (Presses the button of the row containing the keyboard card.) |
| Bob: | Do you know how to make an angle ?… See, these words DISTANCE and ANGLE, are like boxes, and we’re going to put a number in the slot…Make, space, quotes — |
| Miriam: | (Interrupting impatiently) I know! |
| Bob: | You know how to spell “angle” ? It’s here if you don’t. |
| Miriam: | (As she keys) Space…1, 0, 5… new line ? |
| Bob: | Now the distance Robby used last was 100. If that’s a good one we don’t have to change it. |
| Miriam: | Let’s keep 100. |
After this first success with a slot machine POLY procedure, Miriam varied the contents of the variable ANGLE several times.
TWO VARIABLES AT ONE TIME. Miriam had not herself assigned a value to the variable DISTANCE in Logo session 30. As the next Logo session began, both ANGLE and DISTANCE were initialized to default values of zero. After arranging a FORWARD and RIGHT loop on the Slot machine and directing control at the keyboard, Miriam assigned 150 as the value of ANGLE. THe turtle circled in place when she initiated the POLY procedure. Miriam interrupted the loop with a clearscreen and keyboard invocation:
| Bob: | …Control is now at the keyboard. |
| Miriam: | M, A…Why didn’t the hundred and fifty work ? |
| Bob: | What was it was a hundred and fifty ?…The ANGLE box has a hundred fifty in it. Remember, there’s a DISTANCE also. |
| Miriam: | (Frustrated noises.) |
| Bob: | You have to tell the turtle how far to go forward…. Do you know how to spell DISTANCE ? |
| Miriam: | No. |
| Bob: | Here, I will show you….Just key MAKE QUOTES DISTANCE some good number. |
| Miriam: | (As she keys) MAKE QUOTES… |
| Bob: | (As she keys) DISTANCE, yes. |
| Miriam: | Now what ? |
| Bob: | What are you going to put in the slot ? |
| Miriam: | What slot ? |
| Bob: | The slot that’s associated with the name DISTANCE. |
| Miriam: | I don’t know how to do it. |
| Bob: | Sure you do. You did it yesterday. |
| Miriam: | No. I did MAKE ANGLE. |
| Bob: | Well, now do MAKE DISTANCE. It works the same way. The turtle turns. He goes right and turns a number that’s in the slot of ANGLE. When he goes forward, he goes a distance that’s in the slot of DISTANCE. |
Miriam’s first two variable POLY was ANGLE 80, DISTANCE 190. She was delighted with that result and her next trial as well, with ANGLE 150. It is clear that at first she did not know how to MAKE “DISTANCE and did not recognize that it was the “same” as MAKE “ANGLE which she had done the day before. However, with explanation and some direction, she did find accessible the practice of assigning variable values.
During use of the SLOT system, the angle 60 degrees was frequently prominent. After the introduction of a CHANGER operation card (which incremented the variable operand of a forward operation), we made a set of nested hexagons and a hexagonal maze. Her sense of proprietary interest shows its beginning in this dialogue (Logo Session 36, age 6;2;30):
| Miriam: | There…MAKE…(Keys MAKE “ANGLE) |
| Bob: | Do you know any good maze numbers ? |
| Miriam: | I think I’ll try 60. (She keys 60.) |
| Bob: | So you made ANGLE 60. What are you going to make DISTANCE ? |
| Miriam: | (As she keys)…1, 0. |
| Bob: | 10. O.K. What about DELTA ? DELTA’s 4 now. |
| Miriam: | How about 4 ? |
| Bob: | O.K. Let’s leave it alone. |
| Miriam: | New Line. (A POLYSPI 10-60-4 appears). |
| Robby: | Oh wow ! |
| Bob: | That’s a beautiful maze. |
| Robby: | Can we get two prints of it ? |
| Miriam: | Mine. (She keys PRS; this is a PRINT SCREEN command.) |
| Robby: | Daddy, when it’s done, can we get another print of it ? |
| Miriam: | No….Didn’t I do a nice thing ? |
| Bob: | That’s a beautiful maze, Miriam. What angle was that ? |
| Miriam: | 60. |
| Robby: | It’s really a hexagon. |
| Miriam: | Isn’t that a beautiful maze ? |
| Robby: | Why couldn’t we get two pictures of it ? |
| Miriam: | It was my idea. |
Later, in Logo session 43, Robby in his turn generated a “family of mazes,” regular polygonal spirals with angles of 120, 90, 72, 60, 45, and 30 degrees. At the end of that session, Miriam entered my office and seeing his pictures displayed on the wall, objected vigorously that he had used “her” angle of 60 degrees. This complaint could be dismissed as an expression of jealousy at Robby’s achievement and my recognition of it except that it was repeated frequently over following weeks.
My conclusion is that Miriam looked at ANGLE less as a variable capable of assuming a range of values and more as a class name for a collection of objects. If there is no functional difference in such a distinction, there is a difference in salience: seen as a variable, the function is more forward; seen as a collection of quantities, the particular value is dominant. With the former view, relations of variables to objects would focus on transformations of values to artifacts; with the latter, the mere associations of quantities with artifacts is a quasi-nominal rather than transformational relation.
Other Related Experiences Not Leading to Cognitive Integration
In Miriam’s other experiences with polyspiral designs or polyspiral families, there is no indication that she understood what she was doing in any profound way. In contrast with Robby’s work, which showed that he grasped the idea of isolating one variable from a set and exploring the generation of possible designs by stepping (varying incrementally) the value of that variable while holding others constant [note 1], Miriam’s greatest achievement in this direction was imitating a display of his designs, taping them on the wall “in alphabet order, by the numbers” as she put it. Her exploration of possible INSPI designs was interesting to her and engaging but surely empirical in character and in no way integrated with her other turtle geometry experiences.
The conclusion at the end of the core period of The Intimate Study was that she had learned many things but had not learned anything about geometry which could affect her mind or thought in a way beyond what is common in everyday experience. I emphasize that this conclusion applies only to her exposure to turtle geometry [note 2].
Evidence of Later Connection
During the core of The Intimate Study, Miriam did not give evidence of understanding how microviews of the Design cluster related to those of navigation. She could use iteration but there was no evidence she understood it as she so obviously did in this later incident (6;11;15):
As I sat at work in the reading alcove, Miriam came to join me. She offered to sit in my lap, but I protested to being busy and turned her down. Miriam moped a little, then crawled onto my bed and into the center. She began to move and spin in a most puzzling and distracting fashion. “What are you doing ? You’re driving me batty!” I complained. My gripe inspired Miriam to explain. Requesting a pen and a 3×5 card, she drew on it a right rectangular polygonal spiral to show what she was doing in her “crawling on the bed game.” Her verbal explanation was that she was “making one of those maze things.”
Whence came this connectedness in her knowledge of physical action to pattern? My best answer to that question is as follows.
Rods-Maze
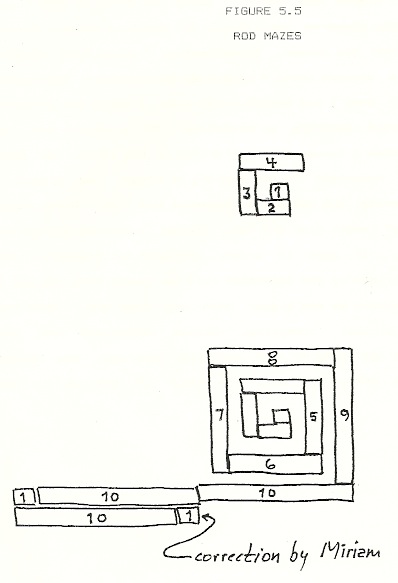
Because I lived with Miriam, it had been an ever present temptation to follow her continuing development. Thus, when one day the children pestered me to play with some Cuisenaire rods I had brought home from the Logo Lab, I agreed on condition that we begin with a project of my choosing. My proposal was this: after they sorted the rods by color (and thus by length as well), I would begin to make something; their problem was to describe what I was making and what my procedure was. I began to construct the object whose development is shown in Figure 5.5.
After I placed four rods, I asked the children what I was making. Robby answered immediately, “A swirl, a maze.” Miriam chimed in with his answer. Subsequently, I asked Robby to hold off on his answers until I discussed my questions thoroughly with Miriam. When I had placed eight rods, I asked the children if they could describe my procedure. Miriam could not, at first, but when I focussed her attention on the length of each piece, she remarked: “You’re growing it bigger and bigger.” Upon questioning, she noted the increment was “one.”
After Robby added rods of length nine and ten, Miriam justified his action by arguing, “It goes in order…littlest to biggest,” and finally described my rod selection rule as “every time you put a rod in, it should be one bigger than the last one.” With the mentioned minimal prompting, Miriam understood well the incrementing of length. In striking contrast, she showed considerable difficulty with the role of turning in the construct.
The Moment of Insight
When I set down the eleven-length (the orange and white pair of rods), I did not orient it perpendicularly to the previous length. Miriam declared the arrangement incorrect but had trouble specifying precisely what was wrong. When she rearranged the rods to place them correctly, she simply interchanged the location of the orange and white rods. From this action, I infer Miriam considered the placement incorrect because two rods of the same color were adjacent to each other — but not because the one rod was colinear with the preceding one. Here I asked Robby to explain what I should have done:
| Robby: | You should go a right 90. It could be orange, right 90, white orange. |
| Bob: | And what should I do after the next orange? |
| Robby: | You probably could do an orange and red. |
| Bob: | (Placing the new rods colinear with those preceding) |
| Robby: | Hold it ! You should do a right again. |
| Bob: | Oh. Miriam, What should I do next? |
| Miriam: | A right 90, green and orange. |
| Bob: | Next? |
| Miriam: | A right 90, purple and orange. |
This is the point at which Miriam brought together in a comprehensible relation the steps and result of a maze generating procedure.
Social Guidance & Personal Insight
If we review this rods-maze experience, several aspects stand out. One is the extensive guidance Miriam received from the microculture. The task she confronted focussed on the articulate description of procedures. When she could not begin, I directed her attention: “Look at the length of each piece.” When she got sidetracked, concerned with color alteration instead of turning, Robby’s description of my error definitely redirected her thought.
One can say of Miriam’s knowledge implicated in the task that she worked with a familiar objective (creating a maze), worked with familiar objects (Cuisenaire rods), and applied familiar operations (adding one to a number, turning right 90, repeating a procedure). I consider these experiences of the rods-maze and turtle on the bed to have integrated and thus culminated the development of Miriam’s knowledge about iteration. The experience was clearly important for Miriam: in later years, whenever offered Cuisenaire rods to play with, constructing a polyspiral maze surfaced regularly as her objective of choice.
I believe this experience with rods helped Miriam better understand her prior computer experiences, but there is no direct evidence to support such a claim. Consequently, the upcoming discussion is admittedly speculative. Nonetheless, I judge it worthwhile because the concrete detail of these experiences permit discussion of issues about the organization of the mind which are much more specific and down to earth than is usually the case.
CONVERGING INTERPRETATIONS
The central issue of human cognitive organization is how long-developing, disparate cognitive structures become linked in communication to form a coherent mind — at least, an information structure sufficiently unified to exhibit the kinds of mental behavior which we experience personally and witness in others. The studies of preceding chapters focussed on microviews which had much in common. The foregoing incident, “Evidence of Later Connection,” presents a concrete linking experience as a possible basis for interconnection between essentially remote clusters of microviews [note 1]. Such a linkage is at least well exemplified — if not well established — in this case. I now take the example as empirical guidance for thinking about how this concrete linking can take place between essentially remote bodies of knowledge. [note 1]
Rods-Maze as Mediator
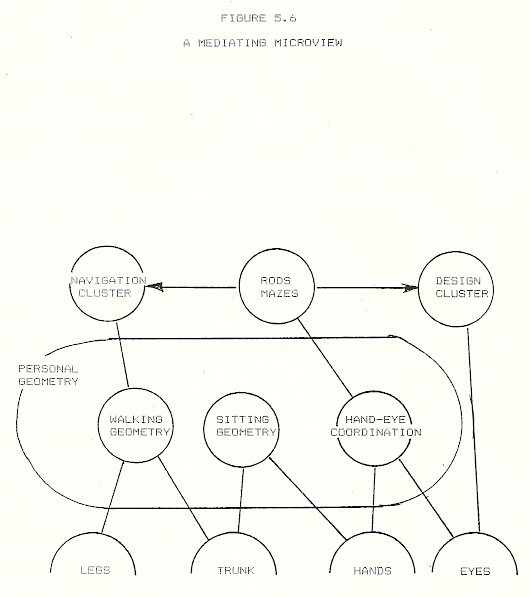
In the preceding studies, I isolated incidents which plausibly could be argued to have been the context of moments of insight where previously disparate microviews were brought into communication. We lack such a certain incident in which this linkage occurred for these turtle geometry microviews [note 1]. The simplest way of describing the linkage is through seeing that the RODS-MAZE microview plays a mediating role. The LOCAL character of Miriam’s learning in the RODS-MAZE incident implies that it was not developed analogically but de novo from more primitive components of the sensori-motor system. My proposal for how we should think of that is shown in Figure 5.6.
Cross Modal Co-ordination
What is it about the character of the RODS-MAZES view that permitted it to function effectively in closing the formerly unbridgeable gap between the cluster of turtle geometry Navigation microviews and the Design cluster? Descended directly from the coordinating scheme which results in hand-eye coordination, the RODS-MAZES view was effective as mediator for two reasons, which can be brought forward in this simple comparison expressing the activity of the primary agents in these microviews:
| LOCOMOTIVE | MEDIATING | VISUAL |
| I MOVE FROM HERE | YOU (HAND) MOVE FROM | THAT (THING) GOES |
| TO THERE. | HERE TO THERE. | FROM HERE TO THERE |
| CENTRAL AGENCY | HAND AS SEEN AGENT | EYE AS ACTIVE AGENT |
| DIFFERENCE: | AGENT | AGENT |
As noted at the end of “Two Geometries,” the primary difference between the active programs of the locomotive and visual subsystems is the level of aggregation which is significant for their functioning. The body lurches forward, step by step. The eye recognizes an image as an entity by circulating repeatedly in the pattern of a closed loop, a “feature ring,” which defines that object in memory. The feature ring program is a complex recognition procedure, whose primitive elements are like the movements of the locomotive system, going forward and turning right. Because of years of developed hand-eye coordination, the eye can recognize the pattern that emerges from what the hand does whereas it can not recognize so simply (if at all) the pattern that emerges from the path of body movement. The RODS-MAZE experience was able to function mediatively between descendents of the locomotive and visual subsystems because the hand, as the familiar agent for manipulating remote objects (say little toy dolls some of whom may be thought of as self or other), can make the bridge between an action of movement which a body might make and one which can be coordinated with visual results.
NUCLEATION OF MICROVIEW CLUSTERS: Minsky’s metaphor
This is not the only possible interpretation. Earlier (Lawler, 1979) I offered another interpretation which I review here because of the more general light it casts on the organization of mind. The alternative interpretation, which I named THE NUCLEATION OF MICROVIEW CLUSTERS, is a generalization of the idea of a Post-cedent Ancestor. Consider all Miriam’s computer-generated design experiences as a cluster of related but uncomprehended microviews. I suggested the special effect of the RODS-MAZE experience could be explained if it was able to function as a “post-cedent ancestor” for all those views. The inference was drawn that over time those empirical microviews would be reconstructed as “logical descendents” of RODS-MAZES. The explanation offered for why this particular experience acted with such force was that it represented in concrete form a “powerful idea.” Since it would be capable of acting as a post-cedent ancestor for all the members of a cluster of formerly related but unlinked microviews, it would be the nucleus of a microview cluster. Here the idea of cluster nucleation was able to link up with another image of cognitive organization from Minsky’s Frames paper. The mind can be seen as an information network wherein the nuclei of microview clusters play the role of geographic capitals in the great world.
In a city, any person should be able to visit any other, but we do not build a special road between each pair of houses; we place a group of houses on a “block.” We do not connect roads between each pair of blocks, but have them share streets. We do not connect each town to every other; but construct main routes, connecting the centers of larger groups. Within such an organization, each member has direct links to some other individuals, mainly at his own “level,” mainly to nearby, highly similar ones; but each individual has also at least a few links to “distinguished” members of higher level groups….
…As our memory networks grow,… our decisions about what we consider primary or “trunk” difference features and which are considered subsidiary will have large effects on our abilities. Such decisions eventually accumulate to become epistemological commitments about the “conceptual” cities of our mental universe…. The selection of capitals corresponds to selecting stereotypes or typical elements whose default assignments are unusually useful….We need not invoke any mysterious additional mechanism for creating the clustering structure. Developmentally, one would assume, the earliest frames would tend to become the capitals of their later relatives, unless this is firmly prevented by experience…. Acquisition of new centers is in large measure forced upon us from the outside: by the words available in one’s language; by the behavior of objects in one’s environment; by what one is told by one’s teachers, family, and general culture….”
Minsky, 1975
The identification of these capitals not as prototypes but as post-cedent ancestors of microview clusters is a unification of the structural metaphor of Minsky with Papert’s theme of powerful ideas — a unification based on my empirical observations about the interacting roles of construction and reconstruction in the everyday processes of natural learning. At this point, even as I abandon the specific interpretation as applicable to this particular case, I maintain the coherence and importance of this idea as a component of a computational vision of cognitive organization.
The Ownership of Ideas
Why is it necessary to supplant the former interpretation of the RODS-MAZE experience with a new one, the channelled description conjecture ? There are two reasons. First, the nucleation of microview clusters did NOT explain why this experience was more powerful than some other might have been in effecting the cognitive reorganization I impute to it. Second, it did not address a major gap in the description of powerful ideas, a gap which I became convinced was essential to close. Specifically, following Papert, I described the RODS-MAZE microview as a concrete model of a powerful idea by attributing to it the characteristics of simplicity, generality, and utility. That is, the objects of the experience (Cuisenaire rods and the square maze) were easily recognizable and distinct entities; the generality of the discovery made through the experience — that through a series of comprehended steps one could create an unexpected but easily recognizable result…the idea of emergent form [note 1] — and its specific utility to Miriam in rendering comprehensible the relation of turtle navigation to computer generated designs, all qualify the experience as the concrete embodiment of a powerful idea. But there is another dimension to ideas to which I had long been sensitive (from the poetry of G.M. Hopkins and Stephen Crane), [note 2] that the ownership of ideas is a critical element in their power for the individual. When completing the thesis One Child’s Learning, I was not able to create a theory which would embrace this observation but still I marked it as an essential element of a theory of mind.
…The leitmotif of ownership [of ideas] running through this disquisition has not emerged clearly as a theoretical theme, but it is irrepressible as an issue because, when the mind is seen as an autochthonous construction of the person, ideas-to-be-incorporated will be intimately owned as few other things in life are….
Lawler, 1979, p.720
In Mindstorms, Papert labelled this dimension of ideas “syntonicity” and emphasized the importance of ideas being personal, but advanced no explanation for why this some times occurred and other times did not, and no proposal for how such a thing might work within a computational vision of mind. The channelled description conjecture does offer such a proposal: concrete embodiments of ideas are personally owned because they are not remote from the shaping structures of the soma itself. Experiences such as those of RODS-MAZES are powerful precisely because they provide the links between late developed structures and the coordinating schemata (the primary integrations of the sensori-motor subsystems achieved during the sensori-motor period). They are important because they link the concrete structures of body knowledge to the more abstract descriptions of external things that blossom as the cognitive network of the mind.
What Makes Some Ideas Powerful and Not Others ?
The Channeled Description Conjecture
The question of what constrains the possibility of some ideas being powerful and others not so is the crux of the channelled description conjecture. In strong form, it proposes that ONLY those concrete embodiments of ideas which link together descendents of disparate sensori-motor subsystems can be powerful; it claims that such models are the correlate in concrete thought of the correspondence schemata of the sensori-motor period and that on them depends the developing coherence of the individual’s cognitive structure. Further, such microviews provide the bases of construction of the more extended cognitive nets of developed minds, functioning as the ancient cities, the geographic capitals of personal importance. In contrast with a goal-oriented attempt to link feelings and thoughts — say upon a basis of disparate need systems as seen in ethology — and with a Freudian focus on the conflict between competing, even conflicting homunculi in the mind, the channeled description conjecture proposes a third model of basically disparate structure, but one better characterized by a pun of Wallace Stevens, “my anima likes its animal,” than by either the needs or conflicts of the other mentioned alternatives.
Learning through Debugging and the Nucleation of Microview Clusters
A final link between two converging visions of mind is the idea of learning through debugging. Sussman (1975) developed a computer-based model of learning which is grows out of a simple but profound observation. In my paraphrase, the idea is: “if you don’t understand something, you can’t tell that it’s different from what you do understand.” The main consequence of this observation is the following general vision of the process of problem solving: not recognizing that a new problem is different from others met before, one first tries old solutions; when these old solutions fail on the new problem, the specific details of the failure provide guidance for the construction of a variation of the old solution which will solve the new problem.
The vision of problem solving as learning through debugging faulty procedures shows directly and lucidly how to think of the incremental refinement of local knowledge. The nucleation of microview clusters attempts to perform the same function on the level of cognitive organization. Consequently, this idea is a further unification of ideas on learning long developing in the MIT Artificial Intelligence community. Their convergence with the results and interpretations of my empirical psychological research coalesce into a vision of the structure of mind that goes beyond a single modality of mind.
Summary and New Directions
In my attempt to address the question of how knowledge is organized in the mind — from a perspective where the constraints of learning are judged most important, I have raised for consideration the body parts mind, an organization of cognitive structures with these main features:
– the structure of the mind and its development are reciprocally generative, in Piaget’s pretty paradox: pas de structures sans genese; pas de genese sans structures.
– the dominant aggregations of knowledge are a specific type of schemata, one which I have called “microviews” (competing, pattern-activated procedures); such structures are internalized “descriptions” of the situations and activities of encountered reality.
– interpreting confusion between two different descriptions of space has led to an uncommon emphasis on the role of cognitive reconstruction in the construction of mind (the importance of cognitive reconstruction should not, however, surprise anyone who takes seriously the memory studies of Bartlett, 1932).
– the novelty of this work is the proposal to take seriously the fact that the body is made of parts and reflect this fact in a vision of body-derived cognitive structures; a key observation has been the reasonably precise sense in which body motion and vision are different and interrelated: visual scan paths (the patterns of eye movement involved in figure recognition) can be thought of as procedures of greater or less complexity formed from movement primitives for the foveal target of the eye similar to those of turtle geometry that can describe the movement of the body in space; where Freudian or Lorenzian models of mind focus on functional structure, I have advanced a vision with a somatic foundation to explain functional differences and relations.
– the primary affective dimension of cognition is the congeniality of structures among themselves; that is, new knowledge may be taken up and effectively applied if and only if it is connectible to what is already recognized as part of the self; the appeal of abstract ideas has a distinct but related basis: the structures of which abstract ideas are expressions are less intimately owned than concrete microviews but can be more thrilling when their power is realized; they can even be accepted as most intimate, in fact, when one experiences powerful ideas as the root of personal coherence.
– finally, in our attempt to answer the question of why particular experiences proved effective in learning and others did not, we have formulated the “channeled description conjecture” which in its strongest form states: the connections between late developed cognitive structures can ONLY occur through the mediation of cognitive descendents of the coordinating schemata of the sensori-motor period.
New Directions: Modalities of Mind
What are they, these modalities of mind ? Galton’s famous survey of his colleagues uncovered the phenomenon named after him, that people can generally describe a dominant mode of the most productive of their thought processes. Einstein thought with images. Piaget held internal dialogues. The three dominant modes are the visual (thinking with images), audile (thinking with words), and motile (thinking in which the sense of body movement and tension plays a significant role). These introspectively witnessed modes of thought map directly onto the major sub-systems of the body-parts mind.
The linguistic and visual systems are the most discriminated, and thinking in their modes is clearly reported by the subjects of Galton and those of others who have found his phenomenon robust. Those whose bias is motile have not discriminated so finely between the various kinesthetic sub-systems.
Only extremely handicapped people might be expected to exhibit thought uniformly dominated by a single mode. Whole people, through the varieties of their experiences, can be imagined to develop quite various minds, each with its own particular balance of thought modalities. With such a point of view one may go beyond thinking about mind as a uniform thing — without making the overly simple direct association of modes of thought with “halves” of the brain. One may accept the evidence of dispersion of representations and procedures within the brain by adopting a richer framework of developmental possibilities, one which saves the fundamental insight of Piaget, that through the activity of the individual the mind constructs itself.
Research Issues
What are the appropriate research questions to ask if one takes seriously the body-parts mind ?
– Is it possible to represent the mind, in the large, in a coherent way with such assumptions? Can one assemble an empirical base for cognitive mapping on a large scale within the individual ? For a specific application of the channelled description conjecture, a reasonably complete cognitive history of an individual would be required, a very difficult record to create. If such a direct test is infeasible now, the body-parts mind organization nonetheless presents a new description of mind onto which behavior can be mapped to address questions now most difficult even to raise.
– what are the modes of an individual mind and why ? How do specific life experiences create the Galton phenomenon ? Is the body parts mind useful in explaining why and how people are different from one another ?
– Is it possible to develop structured information-processing models of mind ? (Such would not be constrained to the single mode models of past decades and would be less amorphous than unstructured cognitive networks.) How would one detail the relations of one subsystem to another and what, precisely, would coordinating schemata have to be like ? (The specific interest in coordinating schemata derives from the central role assigned them by the channelled description conjecture.)
Farther from the paradigmatic research of contemporary psychology are endeavors that might be considered cognitive history and anthropology, asking and trying to answer questions such as how the life experiences of different cultures affects the organization of minds possible within them and to what extent technological change and social intervention may foster homogenization or more extensive differentiation between individual people and different peoples of the world.