Vn119.1 Multiplying by Twenty 1/25/78
The children love to get mail and when an envelope comes addressed
to them, to open it. Each has a bank account concerning which they
receive annual earnings statements. The children opened their mail and
puzzled over the contents — a statement of account number, social
security number, and interest earned for the year with no specification
of the current balance. I checked for the latter because, as I explained
to them, I preferred their remaining ignorant because of their
inclination to blat to their friends what capitalists they are. I went
on that they shouldn’t go about bragging how much interest they had
received. “Why not?” I informed them that anyone knowing their interest
could estimate their capital simply by multiplying the dollar amount by
twenty.
Robby and Miriam realized they could circumvent my not telling them
of their bank balances, and Robby began to do so. Miriam lamented she
didn’t know how to multiply by twenty and received Robby’s promise of
help after he completed his own computation. A few days before he and
I had discussed a good trick for 10 times: just writing down an ‘extra’
zero on the right end of the number. Robby realized he could get the
desired result by doubling the interest (by addition), then adding a
zero. He became confused about manipulating the decimal point during
the 10-fold multiplication, but accepted my procedure for doing do. He
read his balance to Miriam, then went to help her.
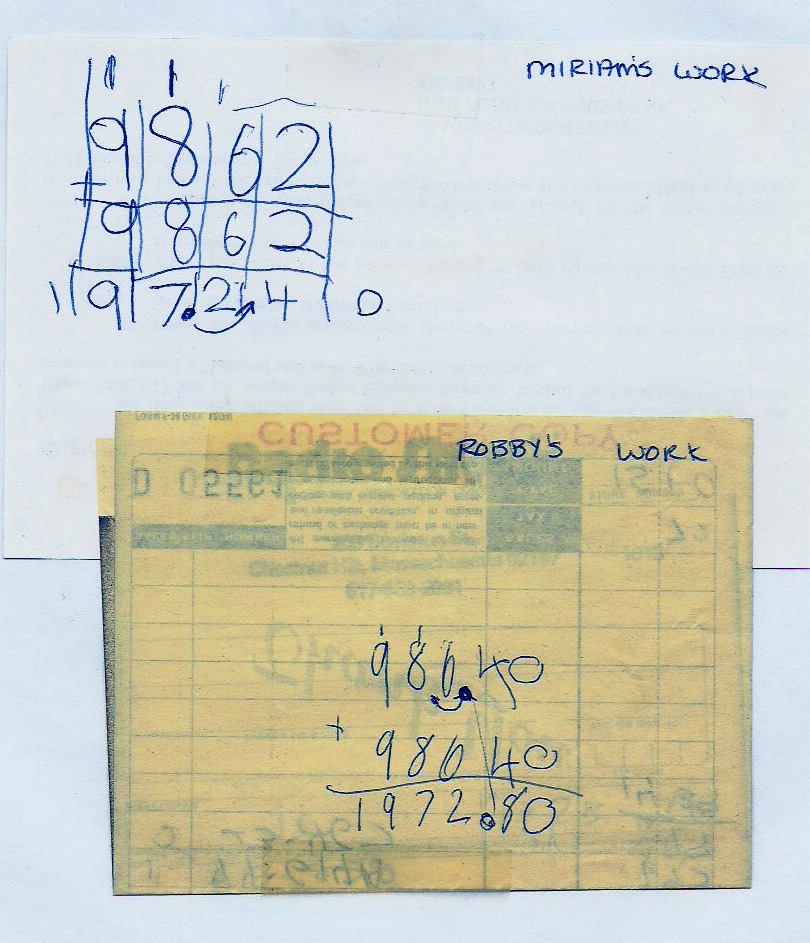
Miriam followed Robby’s direction but set up the problem herself.
My role was limited to restraining him from taking over. No problem
with adding 2 plus 2. The carry first arose with 6 plus 6 (see Addendum
119 – 1). Miriam said, “I put down the 2 and carry the 1.” Robby
responded, “Right.” and when she went to mark a carry over the tens
column, he directed her to place it over the hundreds. With some labor
Miriam added 8 plus 8 and 9 plus 9, handling the carries appropriately.
Thus she had doubled $98.62. But what did the answer mean?
Miriam tried to read her answer 19724: “One thousand. . . one thousand
. . . .” She believed her result should be of the same order of magnitude
as his, but was lost because she could not coordinate that correct judgment,
her accurate computation, and the structure of the problem’s solution.
As Robby did at first also, Miriam neglected the 10-fold multiplication;
nor did she understand at all this good trick for 10 times (she had
never been exposed to it before). Comparing Robby’s work to her own
did not help. Rather than protract her frustration, I “showed” her what
to do. (This means I wrote in the decimal point and an arrow and mumbled
a few words). Miriam accepted my answer as correct and sensible.
Both children were able to rejoice once more at having outwitted
their dumb old Dad.
Relevance
The first incident shows the children applying their arithmetic
skills to a problem too difficult for Miriam. She can effectively execute
complex additions but does not dominate the number representations.
Her writing a carry mark at the top of the tens column shows her sense
that the 1 of 12 still belongs more to the 2 than to the left adjacent
column. I infer that Miriam is working out the problem of what a carry
means. She is very close to understanding. The second incident suggests
I follow up Miriam’s judgment that school arithmetic papers are hard;
why should she find them so?
Addendum
Adding by Miriam and Robby